基于工艺尺寸链中差法的应用*
2014-03-27魏思远
唐 宏,魏思远
(中航工业成都凯天电子股份有限公司,四川成都 610091)
0 引言
在零件加工过程中,当其加工表面的定位基准与设计基准不重合时,需通过建立工艺尺寸链来确定工序尺寸。尺寸链的计算是否正确不仅影响产品质量,而且影响加工制造过程是否经济、合理,因此,正确进行尺寸链的计算是工艺过程不可缺少的重要环节。
在制定零件工艺过程时,经常需用工艺尺寸链来解决基准不重合时求解工序尺寸的问题。工艺尺寸链的原理并不复杂,但在实际运用尺寸链求解工序尺寸时,计算易出错。笔者主要介绍一种基于中差的工艺尺寸链计算方法。工艺尺寸链中差法只需判断封闭环、组成环和待求尺寸,不需判断增环减环即可进行计算,极大减少计算量,节省时间,提高效率。
1 工艺尺寸链基本理论
尺寸链:尺寸链是互相联系且按一定顺序排列的封闭尺寸组。
环:尺寸链中每一个尺寸称为环,尺寸链由组成环和封闭环组成。
封闭环:在零件的加工和机器的装配过程中,间接获得的尺寸称为封闭环,封闭环是间接保证的,且只有一个。
组成环:在尺寸链中对封闭环有影响的全部环。组成环分为增环和减环。
增环:在其他组成环不变的情况下,若某一组成环的尺寸增大或减小,封闭环的尺寸也增大或减小,则该组成环称为增环。
减环:在其他组成环不变的情况下,若某一组成环的尺寸增大或减小,封闭环的尺寸减小或增大,则该组成环称为减环[1-3]。
2 工艺尺寸链中差法的计算方法
2.1 工艺尺寸链常见的计算方法
工艺尺寸链计算方法较常见的解算方法有:极大极小法(又称极值法)、概率法和图解法。
极大极小法:该方法是按误差综合后的两个最不利情况进行的,即若组成环中的增环都是最大极限尺寸,减环都是最小极限尺寸,则封闭环的尺寸必然是最大极限尺寸;增环都是最小极限尺寸,减环都是最大极限尺寸,则封闭环的尺寸必然是最小极限尺寸。
概率法:即应用概率论原理来进行尺寸链计算的一种方法。
图解法:将零件加工的前后所有工序有联系的尺寸链绘在同一个图上,通过对工艺尺寸链的图解,使零件从开始加工到最终检验,全部尺寸的相互关系一目了然,然后根据需要逐项进行计算[4]。
2.2 中差法
基于中差法计算工艺尺寸链与以往的求解方法不同。以上的解算方法都要对尺寸的增环、减环作出准确的判断,且计算易出错。中差法则省去增环、减环的判定,画出工艺尺寸链简图,判断各封闭环、组成环即可进行计算。具体分为三个步骤:①画出工艺尺寸链简图;②判断各环的性质。根据画出的工艺尺寸链简图,确定封闭环、组成环、待求解计算的尺寸;③工艺尺寸链的计算。将所有尺寸全部写成中差“±”偏差的形式。
所求尺寸基本尺寸=总尺寸-其他所有尺寸。
所求尺寸“±”偏差的计算:
若封闭环的公差比组成环公差之和大,则所求尺寸公差=封闭环公差数字-所有组成环公差之和;若封闭环的公差比组成环公差之和小,则须压缩组成环的公差,将封闭环的公差分配到其他组成环上。
3 实例
实例一:如图1所示零件,已知设计基准在B,但由于加工单额工艺性需要,需在B面留余量,以便后工序加工中心加工,因此,在进行车削时,需要把工艺的工序基准转换到基准C上,通过保证A0、A1,间接保证A2尺寸。这样符合实际的加工情况。
分析:
①如图2为工艺尺寸链简图
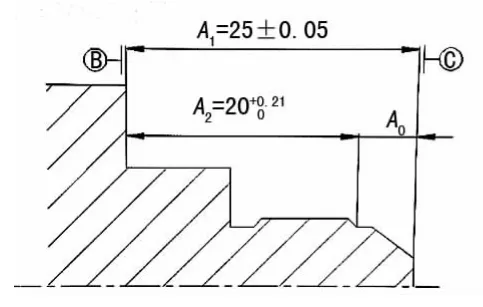
图1 实例一
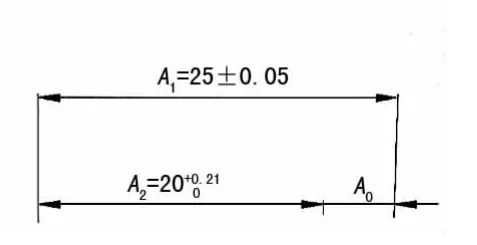
图2 实例一工艺尺寸链简图
②判断各环的性质
封闭环:间接得到底额尺寸是A2,是封闭环;
组成环:A1、A0;
待求的尺寸:A0;
③工艺尺寸链的计算
将所有尺寸写成中差“±”的形式,A1=25±0.05,A2=20.105±0.105,A0的基本尺寸=25-20.105=4.895。
A0尺寸的公差计算:由于0.105>0.05,即封闭环的公差比组成环公差之和大,因此,A0的公差=0.105-0.05=0.055,所以A0=4.895±0.055。
验证,当A1加工到上差25.05,A0加工到下差4.84时,A2=25.05-4.84=20.21;当A1加工到下差24.95,A0加工到上差4.95时,A2=24.95-4.95=20;计算结果均在公差范围内,不会超差,可间接保证A2尺寸,计算方法正确可靠。
实例二:如图3所示零件,已知设计基准在B,现需把工艺的工序基准转换到基准C上,通过保证A0、A1,间接保证A2尺寸。
分析:
①图4为工艺尺寸链简图
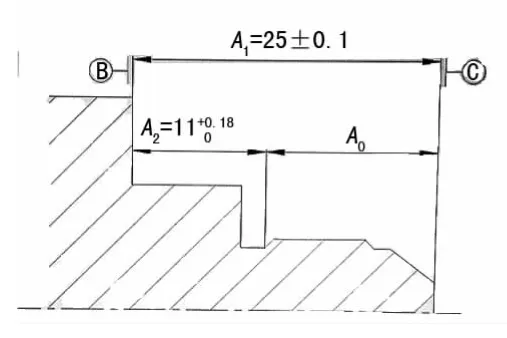
图3 实例二
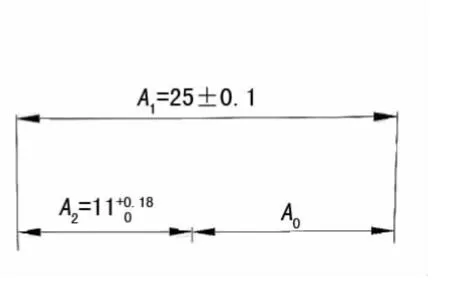
图4 实例二工艺尺寸链简图
②判断各环的性质
封闭环:间接得到的尺寸是A2,因此是封闭环;
组成环:A1、A0;
待求的尺寸:A0;
③工艺尺寸链的计算
将所有尺寸写成中差“±”的形式,A1=25±0.1,A2=11.09±0.09,A0的基本尺寸=25-11.09=13.91。
A0尺寸的公差计算:由于0.1<0.09,即封闭环的公差比组成环公差之和小,则须压缩组成环的公差,将封闭环的公差分配到其他组成环上。在此实例中,把0.09分配给A1公差为±0.05,A0公差为±0.04。
验证:当A1加工到上差25.05,A0加工到下差13.87时,A2=25.05-13.87=11.18;当A0加工到上差13.95时,A2=24.95-13.95=11;计算结果均在公差范围内,可间接保证A2的尺寸,计算方法正确可靠。
值得注意的是,封闭环的公差比组成环公差之和小时须压缩组成环的公差。将封闭环公差分配给其他组成环。分配方式有多种,理论上都可以达到目的。应该根据实际的加工情况,尺寸加工的难易程度进行合理分配。
4 结语
基于中差法的工艺尺寸链计算方法减少了尺寸链计算里面增环减环的判断,只需三个步骤即可计算出所求尺寸的基本尺寸和公差。该方法方法简单易行,还有利于数控编程人员编写数控程序,大大减少了计算量,经验证,计算结果准确可靠。工艺尺寸链中差法是解算工艺尺寸链、确定工序尺寸的有效工具,具有一定的实际工程价值。
[1] 王启平.机械制造工艺学[M].哈尔滨:哈尔滨工业大学出版社,2008.
[2] 邓志平.机械制造技术基础[M].成都:西南交通大学出版社,2008.
[3] 廖念钊.互换性与技术测量[M].北京:中国计量出版社,2007.
[4] 胡凤英.几种典型工艺尺寸链的解算技巧[J].机械研究与应用,2008,21(3):68-69.
