带的强迫共振与主参数共振实验研究*

蔡忠清，李 勇，李路雷，惠 升，马 健，徐培民

(安徽工业大学机械工程学院，安徽马鞍山 243002)

0 引言

动力传送带、磁带、纺织纤维、带锯、带钢、斜拉桥索等的大幅横向振动会影响它们的使用性能，严重时甚至会引发安全问题。引起这种横向振动的因素很多，一般关注的是横向激励引起的强迫共振和系统参数变化引起的主参数共振［1］。当带的长度远远大于宽度时，可将带简化成弦线来研究其横向振动问题［2］。Aitken［3］最早系统地研究了轴向运动弦线的横向自由振动问题。Skutch R.［4］导出了轴向运动弦线的固有频率。Sack［5］讨论了轴向运动弦线在一端边界上受到简谐变化的横向位移激励时的强迫振动响应。亢战等［6］将斜拉桥索与桥面简化成一个二自由度力学模型，通过数值方法研究发现，当拉索某一阶固有频率与桥面某一低阶固有频率的比值在某一连续区间时，桥面振动会激起拉索的主参数共振。符智［7］实验研究了斜拉桥索，当桥面振动频率是某阶固有频率的2倍时会发生主参数共振。Kim［8］对连续热镀锌线上出锌锅上行段带钢在单频参数激励和单频外激励同时作用下的响应进行了数值仿真，发现二者之间存在较强的相互作用，并应用多尺度法研究了和频、差频组合参数共振。李勇［9］以弦线为模型，理论分析了连续热镀锌线上出锌锅上行段带钢子系统的强迫共振以及主参数共振，带钢发生主参数共振时，振动频率是纵向激励频率的1/2，两种共振振幅峰值频率均大于带钢固有频率。

笔者不考虑轴向运动，采用两端简支的模型以阶次跟踪方法［10］实验研究铜带的强迫共振和主参数共振，以验证文献［9］理论分析结果，为后续研究工作提供了实验依据。

1 实验装置

长3 150 mm、宽60 mm、厚0.1 mm的紫铜带上端固定在一钢架的顶部，张紧后下端固定在一块长980 mm、宽275 mm、厚10 mm的钢板中部。钢板两短边固定于钢架底部。钢板上装有一个由伺服电机驱动的铝制辊子。辊子压紧在下端铜带上，如图1所示。辊子及钢板对铜带下端构成了一种柔性支承。更换钢板厚度或在钢板上加重，可以改变柔性支承的动特性。辊子带有一定偏心，转动辊子，既可模拟对铜带的横向激励(支承运动)，又可激发钢板铅垂振动，从而使铜带张力产生波动。改变电机转速，即可调节铜带支承运动及张力波动的频率。

钢架上端自由，下端固结在隔振基础上。安装偏心辊子的钢板装在钢架底部，辊子转动产生的离心惯性力的水平分量几乎作用在钢架底部固定端，对钢架的激扰不大，故可认为铜带的上支承是固定的。所以，两短边固定、两长边自由的钢板、固结在钢板上的偏心辊子以及上端固定、下端与钢板固连、并压紧在辊子上的铜带，这3个元件组成了整个测试对象。

铜带振动由5个涡流位移传感器测量，钢板振动由一个加速度传感器测量，辊子转速(键相信号)由槽型光耦和码盘组成的测速装置测量。以上所测信号均由LMS Test.Lab 9B［11］进行采集与分析。

图1 实验装置示意图1～5.涡流传感器

2 实验及结果分析

图1中，铜带构成了一个相对独立的子系统，辊子及钢板构成另外一个子系统。辊子不转动，并维持铜带张力一定:①横向激扰铜带，测得铜带子系统前三阶弯曲振动固有频率为2.19 Hz，4.37 Hz，6.59 Hz (成整倍数关系，符合弦振动的理论分析);②竖向激扰钢板，测得钢板－辊子子系统的一阶固有频率为14.94 Hz。

保持铜带张力等系统设置不变，设置并启动伺服电机，驱动辊子运转，测试整个系统在升速过程带钢各截面的振动位移和钢板铅垂向的振动加速度随辊子转速的变化规律，以其研究铜带的支承运动和参数激励强迫振动规律。

利用LMS阶次跟踪模块，在40～470 r/min范围内跟踪辊子转速，以3 r/min的转速间隔生成谱阵图。升速速率设定为30 r/min到480 r/min，加速时间为45 s。测得的第一个涡流传感器所在铜带截面(w1)振动位移的谱阵图如图2所示。

图2(b)中的三条光标线对应铜带的前三阶弯曲固有频率。当辊子1倍转频(1 order，即横向支承运动激励频率)接近铜带某阶固有频率时，铜带就会发生强迫共振(振动频率等于横向激励频率)。但截面振动位移的共振峰值频率并非恰好等于铜带的固有频率，而是稍大于铜带的固有频率，如图3所示，其原因是铜带子系统含有较强的因大位移引起的几何非线性，且可以模化为一个刚度渐硬的Duffing系统［8］，此类系统的幅频响应就具有共振峰值频率大于系统固有频率的性能［12］。

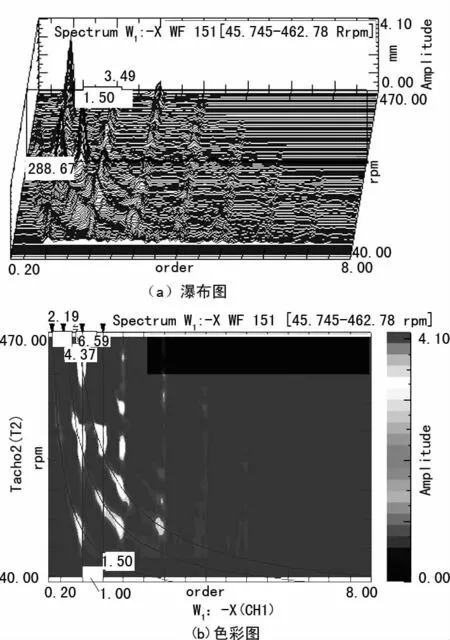
图2 铜带振动谱阵图(阶次8、分辨率0.0625)

图3中辊子转速262 r/min、395 r/min(转频为4.37 Hz、6.59 Hz)分别对应铜带第2、3阶固有频率，由图可见此时该截面(w1)铜带振动幅值并非最大，共振峰值转速分别为288 r/min、430 r/min(转频为4.80 Hz、7.17 Hz)。

图3 1order切片图

图4是钢板z向振动加速度瀑布图，从图中可看到，当辊子转速在264 r/min附近时，钢板会发生以辊子3倍转频为主且振动频率为13.20 Hz的强迫共振，进而引起铜带频率为13.20 Hz的张力波动。并且发现铜带张力波动频率(13.20 Hz)约是铜带第3阶固有频率(6.59 Hz)的2倍，这将诱使铜带发生主参数共振，振动频率为张力波动频率的1/2。图2 (b)中可明显地观察到这一主参数共振现象是在1.5order光标线与铜带第3阶固有频率光标线的交点附近，可看到一个高亮区。这表明，发生三阶主参数共振时，铜带抖动剧烈，甚至甚于二阶支承运动强迫共振。

图4 钢板振动瀑布图(阶次8、分辨率0.062 5)

图5是图2的振动位移谱阵图在1.5 order处的切片图。由图可见，当辊子转速为264 r/min(1.5倍转频6.60 Hz，对应于铜带的第3阶固有频率)时，该截面(w1)铜带振动幅值并非最大，共振峰值转速为290 r/min(1.5倍转频7.25 Hz)。由图2(b)也可看出前述高亮区位于光标线交点的上方。

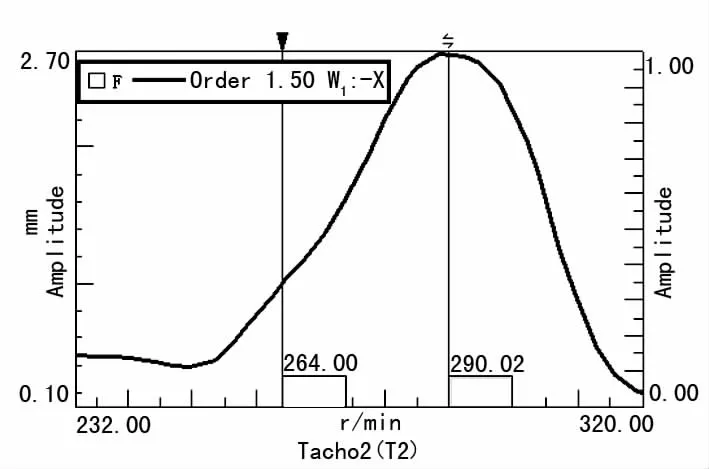
图5 1.5order切片图

说明与二阶支承运动强迫振动共振时一样，发生三阶主参数共振时，截面振动位移的共振峰值频率并非恰好等于铜带的固有频率，也是稍大于铜带的固有频率。原因也是由于铜带子系统是一个刚度渐硬的Duffing系统。

图6是铜带截面(w1)振动位移的时域图。没有触发时，时域信号是有记录的，所以图中截取的是辊子转速40～470 r/min所对应的时域信号。

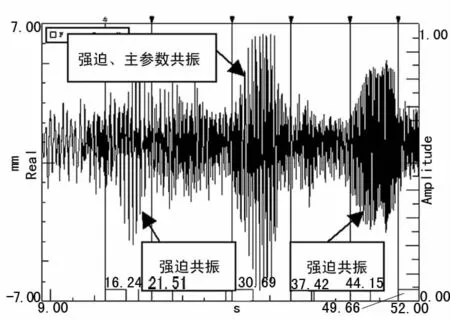
图6 铜带振动时域图

可看出共振区振动幅度明显大于非共振区。从图2(a)中可看到，在辊子转速288 r/min附近，铜带的二阶强迫共振与三阶主参数共振同时发生，使得此时铜带振动幅度明显大于铜带其余阶强迫共振。

3 结语

以阶次跟踪方法实验研究了带的强迫共振和主参数共振。结果表明带的强迫共振频率等于横向激励频率，主参数共振频率为张力波动频率的1/2，并且两种共振振幅峰值频率均大于带的固有频率。与文献［9］理论分析相符，二者得到了相互验证，为后续研究工作提供了实验依据。

［1］ Xu P M，Wang B，Ye J J，etc.Research on the Vibration of Sheet Metal near the Zinc Pot Area in Continuous Hot—dip Galvanizing Line［J］.Applied Mechanics and Materials，2012(141):471－477.

［2］ 刘延柱，陈立群，陈文良.振动力学［M］.北京:高等教育出版社，2011.

［3］ Aiken J.An Account of Some Experiments on Rigidity Produced by Centrifugal Force［J］.The London，Edinburgh，and Dublin Philosophical Magazine and Journal of Science，1878，5(29):81－105.

［4］ Skutch R.Uber die Bewegung Eines Gespannten Fadens，Weigcher Gezwungun ist，Durch Zwei Feste Lpunkte，mit Einer Constanten Geschwindigkeit zu gehen，und Zwischen denselben in Transversal Schwingungen von gerlinger Amplitude Versetzi Wird［J］.Annaien der Physik and Chemie，1897，61:190－195.

［5］ Sack R A.Transverse Oscillations in Traveling Strings［J］.British Journal of Applied Physics，1954(5):224－226.

［6］ 亢 战，钟万勰.斜拉桥参数共振问题的数值研究［J］.土木工程学报，1998，31(4):14－22.

［7］ 符 智.斜拉桥拉索的参激振动研究［D］.天津:天津大学，2009.

［8］ Kim C H，Lee C W，Perkins N C.Nonlinear Vibration of Sheet Metal Plates Under Interacting Parametric and External Excitation During Manufacturing［J］.ASME J，Vib.Acoust，2005，127:36－43.

［9］ 李 勇.带钢—辊子及其柔性支承混杂系统的非线性耦合振动研究［D］.马鞍山:安徽工业大学，2009.

［10］ 李方泽，刘馥清，王 正.工程振动测试与分析［M］.北京:高等教育出版社，1992.

［11］ LMS国际公司北京代表处.集成的振动噪声与试验平台［J］.CAD/CAM与制造业信息化，2008(7):51－53.

［12］ 胡海岩.应用非线性动力学［M］.北京:航空工业出版社，2000.