静电场中电场强度的多极展开

崔明，崔元顺

(1.淮阴工学院 人事处，江苏 淮安 223003;2.淮阴师范学院 物理与电子电气工程学院，江苏 淮安 223300)

0 引言

电磁场中的多极展开方法与内容主要涉及静电场的电势、稳恒磁场的磁矢势及辐射场的推迟势等方面，无论是在理论物理研究，还是在工程技术应用中都具有十分重要的地位，例如，在原子结构与光谱学中，原子核与外场相互作用能级或光谱的超精细结构需要考虑原子核的高阶极矩表示;在分子物理中，单个一氧化碳分子、氟化氢分子是纯粹的偶极分子代表，二氧化碳即是典型的纯粹线形四极分子;在非线性光学中，需要考虑电偶极矩乃至电多极矩对外加周期性变化电磁场的非线性响应特性;在无线电物理中，各种利用微波技术的天线发射与接收、电磁散射与逆散射、测井技术、探矿等等领域得到广泛应用［1－8］。已有文献表明［9－11］，在涉及电磁场中多极展开问题时几乎都是采用势函数的办法，本文不同于现有文献，试图另辟蹊径，就静电场问题，直接从电场强度矢量的叠加原理出发，着力于研究小区域中电荷分布在远区产生电场强度的多极展开过程，给出一些新的公式与结果，为相关场合下的需要提供参考。

1 电场强度的多极展开

在真空情况下，当空间有限区域V中分布连续电荷ρ(r')时，由此电荷在场点r处产生的电场强度为［9］

其中，体积分遍及电荷分布的区域，场源 r'到场点 r的位置矢量为 R=r－r'，而距离R=，如图1所示。

依据(1)式中被积函数形式，对函数r/R3的每个直角坐标分量分别按照(2)式进行处理。令

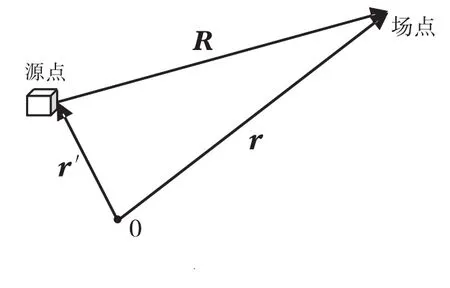
图1 物理模型

即

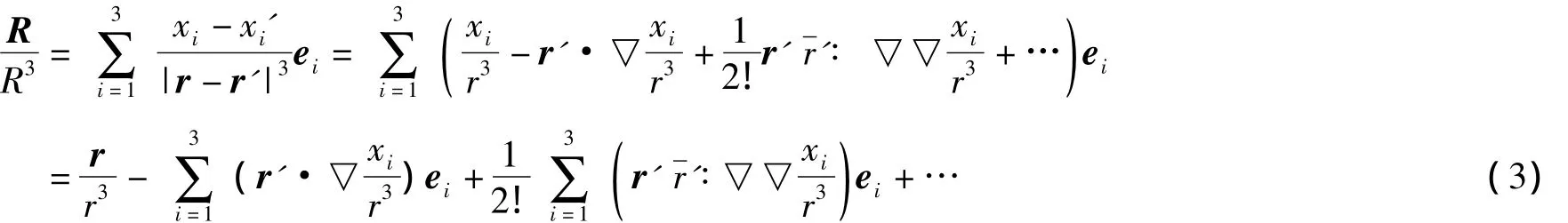
其中，两点“∶”代表并矢间的二次内积。对于(3)式中的第二部分，因为2r=er、2xi=exi，有

故矢量和为

其实，利用关系r'·(2φ)=(r'·2)φ，(3)式中的第二部分也可以直接由下式给出

同样地，对于(3)式中更高阶的第三部分，仿效上述运算有

化合物 3B08：质谱 ESI／MS（negative mode），m／z 273，［M－H］－。 1H NMR（500 MHz，CDCl3，TMS），δ为8.59（s，1H），8.34（d，J＝8.0 Hz，1H），8.16（d，J＝8.0 Hz，1H），7.64（t，J＝8.0 Hz，1H），7.31～7.34（m，2H），7.03（t，J＝8.5 Hz，2H），6.75（br.s，1H，NH），4.62（d，J＝6.0 Hz，2H）。

综合以上计算，给出对应于多元函数标量展开(2)式的矢量展开式为

将(7)式代入(1)式，可得电场强度的展开结果为

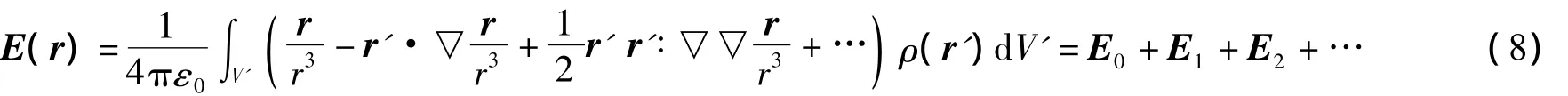
其中

2 结果分析

现在对(8)式中展开结果的各主要项进行分析与讨论，并阐述其物理意义。

若定义体系的电偶极矩矢量为

(14)式即置于坐标原点的电偶极矩P在远区产生的静电场强度。此外，因为，故可以将(14)式改写为

依据E=－2φ关系，不难给出该电偶极子在远区产生的静电势

对于(11)式，若定义体系的电四极矩并矢为

故(18)式可以改写为

借此可以给出该电四极矩产生的静电势为

将(16)式、(20)式等关系与采用电势展开方法所给出的表达式比较，可见结果完全一致［9］，表明上述的计算过程是可靠的。

3 结束语

本文不同于电势函数的方法，直接以电场强度的积分表达式(1)式作为出发点，研究小区域中电荷分布在远区产生电场强度的多极展开方法，给出其处理过程与技巧。除了(9)式之外，用各阶极矩描述电荷分布偏离球对称的程度，用置于坐标原点的各阶极矩产生的电场强度逐步逼近其真实的结果。借助于常见的极矩定义(13)、(17)式，直接给出电场强度矢量的表示(14)、(18)式。此外，为了考察计算的可靠性，便于同电势展开结果作比较，文中还给出了与电场强度相对应的电势表示式。文中对展开式每项代表的物理意义进行了分析探讨，对于相关的教学及应用具有一定的参考价值.

［1］张春早，武奇.电四极矩及其在原子核物理中的应用研究［J］.安徽师范大学学报(自然科学版)，2010，33(3):247－249.

［2］孔静，严继民.势诱导原子多极矩分布［J］.科学通报，1990，11:824 －827.

［3］沈韩，张鸿，李景德.量子化学计算中的电偶极矩［J］.哈尔滨理工大学学报，2003，8(5):8－15.

［4］朱梦，周辉，程引会，等.两种深空核爆炸辐射电磁脉冲模型的比较［J］.原子能科学技术，2013，47(6):897－900.

［5］杨福家.原子物理学(第3版)［M］.北京:高等教育出版社，2000.

［6］梁昌洪，陈曦.电荷多极子和电流多极子［J］.电气电子教学学报，2011，33(4):1－5.

［7］崔元顺.用磁矢势并矢格林函数研究旋波媒质中的电波辐射［J］.微波学报，2000，16(3):256－259.

［8］崔元顺，刘洪香，李建华，等.计算电磁场多极展开的直接方法［J］.大学物理，2013，32(10):17－20.

［9］郭硕鸿.电动力学(第3版)［M］.北京:高等教育出版社，2008.

［10］陈惠青.电磁波理论—无坐标方法［M］.梁昌洪，刘鹏程，李天成，等译，北京:电子工业出版社，1988.

［11］刘健平.电势多极展开的一种导出方法［J］.西南师范大学学报(自然科学版)，2010，35(6):185－189.