一个新的就地稳定归并算法

胡圣荣

(华南农业大学 工程学院，广东 广州 510642)

0 引言

在计算机科学与实践中经常遇到归并问题，它是外排序的基础，在内排序中则可构成归并排序。另外，一些并行排序算法也经常采用归并的方法;在各种排序网络中，基于归并的排序网络比较简单而实用。

在经典内排序方法中，时间复杂性(即使最坏)为O(nlog2n)且稳定的只有归并排序，但它需要O(n)的辅助空间。为此很多文献研究附加空间少的归并算法，如就地归并，其中常用的一个方法是“内部缓存”技术［1-2］;同时为保证时间性能，还会用到一些其它技术，如邻块交换的旋转算法、连续交换中的浮洞技术［2］等。不难发现，很多算法过于追求“就地”与“线性性能”，结果比较复杂，而线性因子也可能较大，并不适合归并排序;还有些不再是稳定的。较典型的有Geffert等的稳定算法，最多m(t+1)+n/2t+o(m)次比较，5n+12m+o(m)次移动［2］，其中m≤n，t=「log2(n/m)」。这类算法中 Kim 的实现［3］有一定实用性，但仍很复杂。若放松严格的“就地”要求，允许O(log2n)的附加栈空间，如文Ellis和 Markov的ShuffleMerge算法［4］，虽不是线性的，但算法简洁实用。Dalkilic的实现［5］则进一步提高了时空性能和实用性。

本文给出一种简便的就地归并算法，附加空间O(1)，比较次数为理论上的最少m+n-1，但移动次数略多。

1 算法

基本思想:设初始待归并区间为A［i，j)、B［j，to)(它们存放于同一数组R中)，对两者从前向后扫描，设当前位置分别为i、p，在［j，p)之间形成动态存储区，存放之前归并比较时前段区间的较大者，即这些元素后移形成缓冲区，它们大于或等于A区间已归并好的部分，把它们组织成循环队列Q，队头指针为f，见图1(a)，于是:

(1)若Q［f］≤B［p］，则Q［f］出队，放到A［i］位置，原A［i］入队，见图1(b)。否则，

(2)Q循环左移使队头位于缓冲区开始位置(以下简称理顺操作)，B［p］移到A［i］位置，原A［i］入队，队长增1，见图 1(c)。

该过程进行中可能出现两种情况:

(1)若原A区间已处理完，则把Q理顺作为新的A区间，与p开始的B区间继续归并。

(2)若原B空间已处理完，则把Q理顺，归并结束。

按以上方法，每比较一次，必定有一个元素到位，比较次数最多m+n-1次。如果Q中不出现理顺操作，则每个元素最多入队、出队1次，移动量最好O(m+n);但一般要多次理顺队列，移动量最坏O(mn)。

该过程不破坏稳定性。归并算法如下:

L1:while(i＜ j＆＆R［i］＜ =R［j］)i++;

L2:if(i＞=j)结束返回;

L3:交换 R［i］和 R［j］，形成初始队列;i++;p=j+1;

L4:while(i＜j＆＆p＜to)

if(队头 ＜ =R［p］){队头出队并置于 R［i］，原 R［i］入队，i++;}

else{理顺队列，将 R［p］置于 R［i］，原 R［i］入队，i++;p++;}

L5:if(p ＞ =to){理顺队列;交换 R［i，j)和队列区 R［j，p);结束返回;}

else{理顺队列;i=j;j=p;转 L1。}

其中理顺队列可通过交换队头的前后两部分R［j，f)和R［f，p)来实现，这是相邻块交换，可用移动量较少的旋转算法［2］实现，它交换长度为m、n的相邻两块移动量为m+n+GCP(m，n)，其中GCP为求最大公约数。

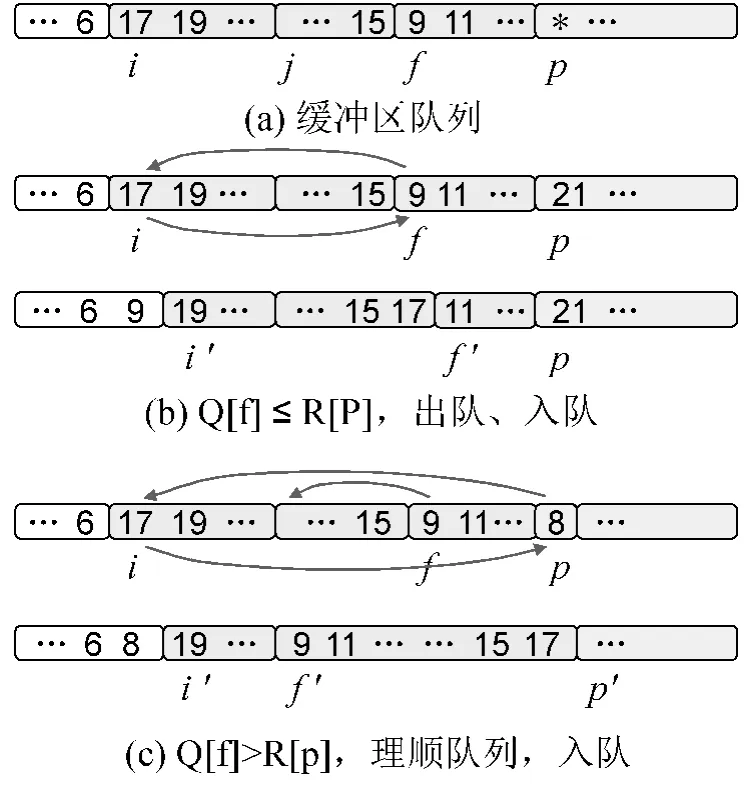
图1 归并算法原理

2 性能分析与测试

对归并算法的测试，通常取2个随机序列，分别排序后再归并，考察归并时比较次数、移动次数等［3-6］。本文采用另一种较简便的做法:将归并算法用于归并排序，考察排序的比较次数、移动次数，这是因为归并排序要大量调用归并过程，更易反映归并的总体性能(文［4］也考察了归并排序，但没有从排序结果“折算”归并结果，见下述)。

上述算法归并两个等长段时，设段长为t/2，则比较次数为O(t)，移动次数最坏O(t2);用于归并排序时，设规模为n，则比较次数为O(nlog2n)，移动次数最坏O(n2)(参见下面归并和归并排序两者复杂性的关系)。下面通过测试来考察算法的平均性能。这里取文［6］的归并算法进行对比(重写代码，以下称算法［6］，基本思想是将后段前部的较小部分交换到前段未归并部分之前，通过旋转算法实现。可能排印瑕疵，文［6］原算法比较次数有多余)。

测试时对随机序列进行排序，由于C/C++系统随机函数rand()范围0～32 767，当规模很大后出现重复，这里采用文［7］的长周期随机函数，各规模下测试若干组随机序列后平均。与文［7］不同的是，这里不通过改变种子来获得不同序列，而是在长周期随机序列中依次截取所需长度的子序列(通过rand()改变种子最多可生成32 767组不同随机序列(要排除rand()=0的情形)，而本文序列组数会远大于此数)。组数的多少自动调整:最多106组，以该规模总排序时间不超过1分钟为准(该时间根据硬件条件设置)但最少10组。结果见表1，其中C、M、T表示关键字比较次数(106)、移动次数(106)、实际运行时间(秒)，其中运行时间包含了比较次数、移动次数的累计时间，这相当于人为地将比较、移动操作增加了一点“延时”。

表1 归并排序结果对比

从表1可见，在测试范围内，与算法［6］相比，本文比较次数相同，移动次数、实际运行时间等都较少，规模较大后约为后者1/3左右。

采用更多测试数据(略)，进行类似文［8］的稳定性拟合，本文比较次数约为1.44nln(n)-1.24n，移动次数约为n2/24;算法［6］移动次数约为n2/8。

下面由归并排序结果反推归并结果:设归并长为t/2的等长两段(归并后长t)的复杂性为f(t)，在归并排序中分别对长n/2的2段归并1次、长n/4的4段归并2次、…、长1的n段归并n/2次，所以归并排序的复杂性为

类似，若规模为2n则有

式(2)-2×(1) 得f(2n)=T(2n)-2T(n)，也即f(n)=T(n)-2T(n/2)。

由排序的移动次数T(n)≈n2/24知归并的移动次数f(n)≈T(n)-2*T(n/2)=n2/48。由排序的比较次数T(n)≈1.44nln(n)-1.24n，知归并的比较次数f(n)≈T(n)-2*T(n/2)=1.44nln2≈n，与理论结果一致。

3 结论

就归并而言，本文算法具有简便、稳定、就地进行、比较次数最优的特点，只是移动次数为二次，不适合用于归并排序(大规模时)。也正是因为移动次数为二次，算法尚有很大的改进空间，其中一个工作是优化、改进缓冲区的数据组织，拟后续进行。

［1］Kronrod M A.Optimal ordering algorithm without operational field［C］//Soviet Math.Dokl.1969，10(744-746):342.

［2］Geffert V，Katajainen J，Pasanen T.Asymptotically efficient in-place merging［J］.Theoretical Computer Science，2000，237(1):159-181.

［3］Kim P S，Kutzner A.On optimal and efficient in place merging［M］//SOFSEM 2006:Theory and Practice of Computer Science.Springer Berlin Heidelberg，2006:350-359.

［4］Ellis J，Markov M.In situ，stable merging by way of the perfect shuffle［J］.The Computer Journal，2000，43(1):40-53.

［5］Dalkilic M E，Acar E，Tokatli G.A simple shuffle-based stable in-place merge algorithm［J］.Procedia Computer Science，2011，3:1 049-1 054.

［6］范时平，聂永萍，汪林林.一种基于数据块交换的快速稳定原地归并算法［J］.重庆邮电学院学报(自然科学版)，2004，16(4):93-96.

［7］胡圣荣.关于排序算法的随机输入序列［J］.武汉理工大学学报，2006，28(9):105-107.

［8］胡圣荣.关于排序效率的数值估计［J］.广州城市职业学院学报，2008，2(1):61-64.