高精度V棱镜折射仪光机结构设计
2014-03-27郭晓雪安志勇
曹 秒,郭晓雪,柳 鸣,安志勇
(1. 长春理工大学 生命科学技术学院,吉林 长春 130022;2. 长春理工大学 光电工程学院,吉林 长春 130022)
引言
光学玻璃折射率是光电仪器中光学系统设计的重要依据,其精度高低直接关系到光学系统的设计质量与成像质量好坏。因此,在制造光学玻璃以及检测设备中,光学玻璃的折射率指标在很大程度上影响光学仪器的质量[1-2]。因此,诸多光学玻璃生产厂家急需高精度V棱镜折射仪服务于光学玻璃生产线的检测环节,以便得到高质量的光学玻璃。本文通过全面考虑影响光学玻璃折射率测量的因素,研制出测量精度为 ±3×10-6的高精度V棱镜折射仪以满足使用要求。
目前,国内V棱镜折射仪可以达到的最高测量精度仅为 ±3×10-5[3]。本文对原有的V棱镜折射仪的机械结构进行改进,将原有的机械测角编码盘改为光电编码器测量折射角,其测角精度由原来的 ±3″ 提高到 ±1″。人眼夹线对准改进为基于 CCD 成像技术的机器视觉对准。为提高成像质量,利用光栅单色仪从氙灯光源中得到足够光强的单色光进行测量。上位机根据测量所得的折射角直接计算出待测试样的折射率。同时考虑空气折射率的影响,给出了修正的原理公式,在此基础上,分析了系统的各项误差,结合实验验证,证明了设计的合理性。研制的高精度V棱镜折射仪对提高光学玻璃折射率的测量精度具有很重要的现实意义。
1 全自动V棱镜折射仪结构组成
高精度全自动V棱镜折射仪主要由准直光管、传动机构、锁紧、微调机构、轴角编码测角机构和CCD 相机等组成,其主要组成部分如图 1 所示。

图1 高精度V棱镜折射仪结构图Fig.1 Structure drawing of high precision V-prism refractometer
根据高精度全自动V棱镜折射仪 ±3×10-6的设计要求,其光机系统关键技术参数如表 1 所示。

表1 高精度V棱镜设计指标Table 1 Design index of high precision V-prism >refractometer
所设计的高精度全自动V棱镜折射仪采用光电式轴角编码器取代了传统的光学细分式度盘,利用 CCD 成像对准技术取代了传统的人眼观察。结合新的功能要求,更新了原有的机械结构形式,设计了机械传动结构、锁紧和微调机构,以及轴角编码测角和 CCD 视觉等集成结构。仪器将原有的准直光管口径和焦距扩大,以满足 404 nm~766 nm光谱范围内成像清晰,并保证 d 光至 g 光成像的调制传递函数在 120 线对数时均在 0.2以上。
2 全自动V棱镜折射仪光机系统设计
2.1 准直光管设计
光学系统采用透射式光学系统如图 2 所示。为了满足宽光谱范围内波差、倍率色差与畸变等像差要求,在传统摄远物镜结构的基础上进行了改型设计,从而达到了很好的像质。
光学设计结果参数为:入瞳口径φ15 mm,焦距85 mm, 视场±3°。如图3所示,在96 lp/mm 处MTF=0.2;全视场内最大波像差均方值小于λ/4;倍率色差小于 2.08 μm,最大相对畸变小于0.05%。为使系统结构紧凑,在光学系统光路中增加了分光棱镜来实现分光观察,原理如图 4 所示。

图2 准直光管光学系统Fig.2 Optical system of collimator
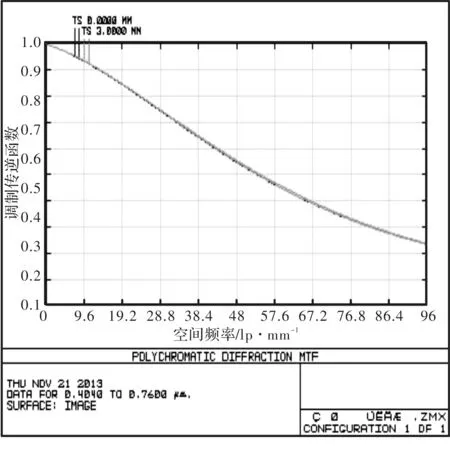
图3 系统MTF曲线图Fig.3 System MTF curve
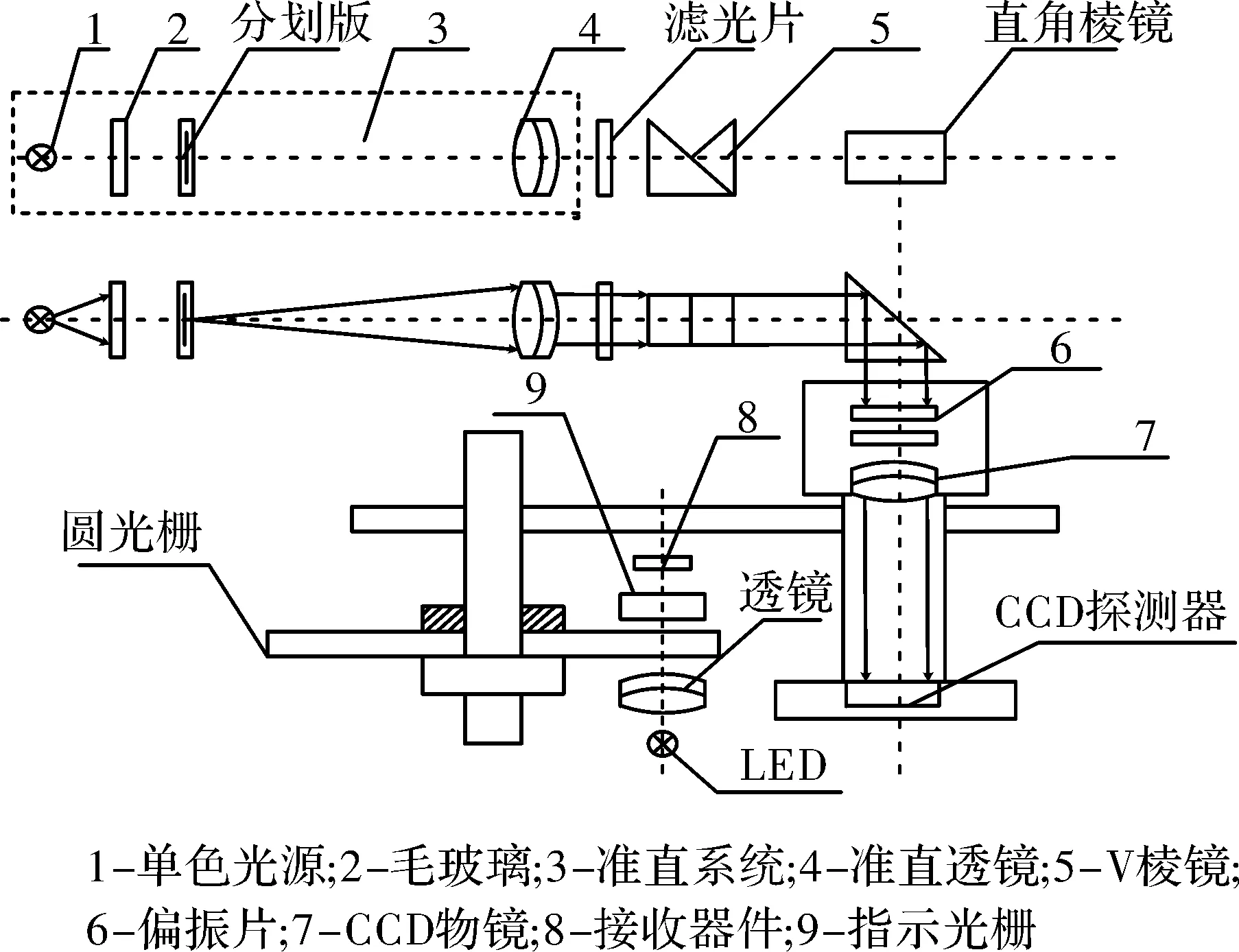
图4 全自动V棱镜折射仪工作原理Fig.4 Working schematic diagram of automatic V-prism refractometer
2.2 机械结构总体设计
高精度全自动V棱镜折射仪结构如图 1 所示。为了减小整体机械结构尺寸,在光路中安装有折光棱镜。考虑到 CCD 成像时单线图像位于一对参考线中间,实现精确对准难的特点,设计有精密微调、锁紧机构。
2.2.1 传动机构
当 CCD 俯仰摆动实现机器视觉对准时,V 棱镜折射仪传动机构对光电式轴角编码器测量偏折角的精确度至关重要,设计时重点考虑2个方面的问题:① 材料和机械结构的稳定性;② 调试的平稳性。为此,V 棱镜折射仪传动机构设计结果如图 5 所示。
考虑设备采用编码器分辨率精度较高的特点,传动中采用齿轮传动可在装调时实现逐级细分以配合轴角编码器的分辨精度。为实现平稳传动并满足强度要求,齿轮模数取 0.5,粗调时传动机构的传动比为 476/52。光电编码器输出轴配有深沟球轴承以减小径向载荷。
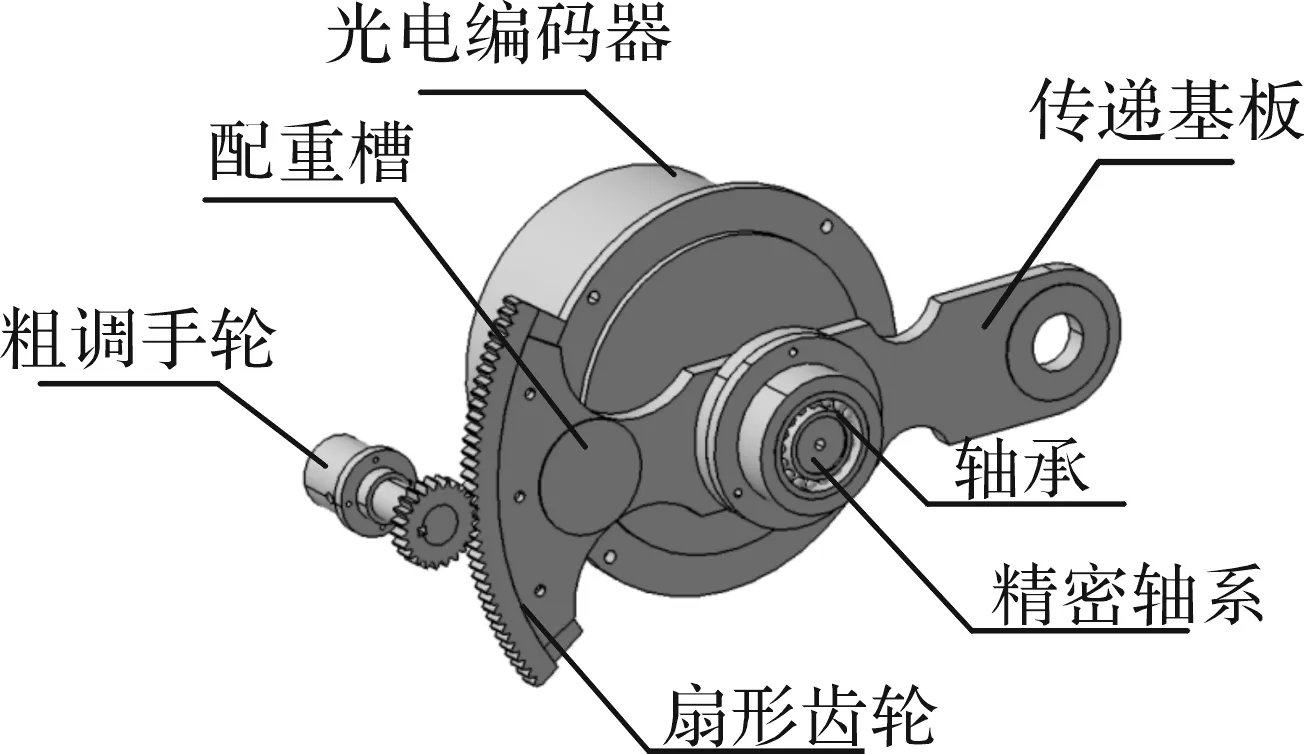
图5 传动机构Fig.5 Transmission mechanism
2.2.2 锁紧和微调机构
为了使光电编码器的输出轴缓慢平稳地微量移动,并将其调整到所需精确位置,故在设计微调机构时采用螺旋传动微动微调机构,按照微应力装夹方法设计有锁紧机构。其结构如图 6 所示,编码器输出轴通过配有橡胶垫的夹紧环固定在安装座上。微调机构采用单向接触法,拉簧通过下夹紧环使螺旋副始终在单向轴向力作用下,保证螺旋副单向接触,其间隙不会引起空程。微调机构的传动比K和灵敏度ΔP为
(1)
式中:D为手轮直径;P为微动螺杆螺距,且P=0.5 mm,R、L如图6所示,传动比K=500。
(2)
人手灵敏度 Δφ取 0.25°, 灵敏度ΔP可达0.3″。
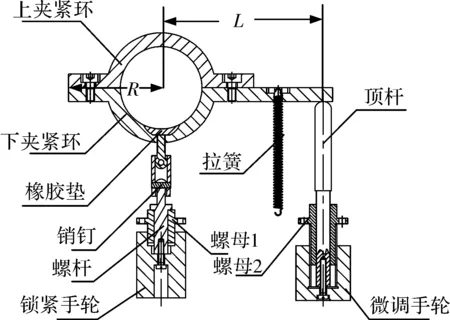
图6 锁紧和微调机构Fig.6 Locking and fine adjustment mechanism
3 仪器精度分析
折射率测量值的测量误差来源主要有3种:①空气折射率引起的系统误差;②偏折角θ的标准偏差引起的测量误差;③V棱镜折射率n0的测量标准偏差引起的测量误差。
3.1 空气折射率引起的误差
对折射率精密测量的研究有很多[4-7],但是对环境条件修正公式的研究就相对较少[8-9]。对于高精度的V棱镜折射仪,不同测试环境如温度、气压、湿度都会影响空气折射率,从而引起测量误差。考虑空气折射率影响因素后的修正原理公式为
(3)
式中:n为被检试样的折射率;n0是V棱镜的折射率;θ是出射光相对入射光的偏折角;nr为空气折射率。
法国物理科学家埃德勒得出的空气折射率计
算公式[10]:
1-f·(3.802-0.038 4σ2)×10-8
(4)
式中:nt,p,f是空气折射率;ns是标准条件下待测试样的折射率;P为气压;t是环境温度;f为环境湿度;σ是真空中波数。
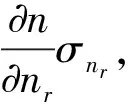
(5)

表2 标准环境条件下各光谱空气折射率引起的误差Table 2 Error caused by air refractive index of different spectra under standard enviroments
由上表可知,V 棱镜折射仪经典原理公式将空气折射率近似为真空折射率所引起的原理误差已超过 2×10-5,将空气折射率引起的误差带入修正后的计算公式,即可以修正测量结果,以达到高精度测量的目的。
3.2 偏折角θ的标准偏差引起的误差
3.2.1 精密轴系误差
光电式轴角编码器的输出轴采用半运动式结构,结构的尺寸参数如图 7 所示。由于轴系配合间隙Δd而使轴系产生角晃动,轴系偏离理想轴线的最大晃动角度Δr为:
105=2.96″
(6)
式中:Lc是主轴下端面至钢球球心之间的距离;dz是主轴轴颈的直径;d0是钢球直径;ρ为将弧度化为秒的换算系数,且ρ=2×105(″)。

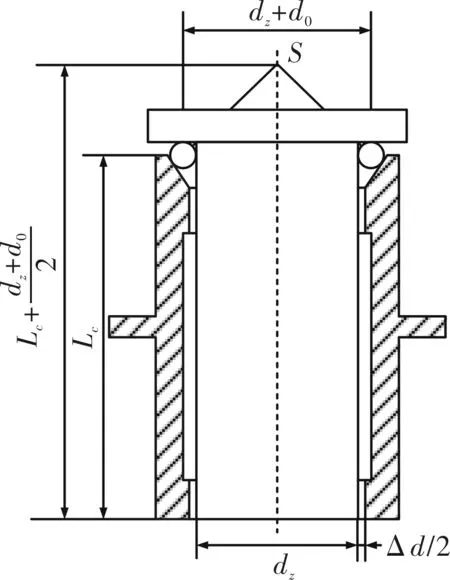
图7 主轴晃动示意图Fig.7 Spindle shaking schematic diagram
3.2.2 CCD 细分误差
像元尺寸为 5.2 μm,出射光线与屏幕预置的双线中间对准时,CCD 光学系统焦距为 20 mm,细分误差取像元的一半,服从均匀分布,则 CCD 细分标准偏差σ2为
(7)
折射角θ的标准偏差σθ为
(8)
式中σ3=1″为光电编码器标准偏差。
将修正后的原理公式(3)对θ求偏导,进而可得θ的标准偏差引起的测量误差:

2.825 73×10-6
(9)
3.3 n0 的标准偏差引起的测量误差
n0的测量标准偏差σn0用光电式精密测角测定,其误差不超过1×10-6。将公式(3) 对n0求偏导,可得n0的标准偏差引起的测量误差:
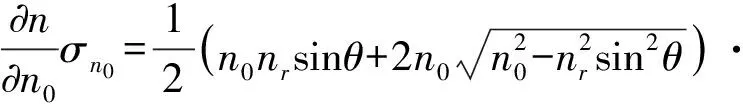
1.007 598 7×10-6
(10)
则折射率测量误差σn为
3×10-6
(11)
由(11)式可知,本V棱镜折射仪折射率检测精度为±3×10-6,高于目前国内外折射率测量装置的测量精度[3,11-13]。
4 实验与结果分析
为得到F、C、d、g、e 5种不同光谱的单色光源, 系统采用全光谱氙灯, 其光谱范围为 400 nm~700 nm。并在5种不同光谱下,分别对标准块的折射率进行了测量,测量结果如表 3 所示。从表 3 中可以看出, 被测试样折射率测量值与标准值比较,误差小于 ±3×10-6。

表3 标准块的折射率Table 3 Refractive index of standard block
5 结论
系统对原有V棱镜折射仪的光机结构进行了改进,在传统摄远物镜结构的基础上改进了准直光管光学系统以满足宽光谱的检测要求;微调机构采用螺旋传动微调机构,按照微应力装夹方法设计了锁紧机构,并将原有的光学度盘测角改为采用光电编码器测量出射光线的偏折角,大大提高了测角精度,使其测角精度从原有±3″提高到±1″。经过实验验证,V棱镜折射仪的测量精度提高到了3×10-6,处于目前国际先进水平。
[1] Yu Daoyin, Tan Hengying. Engineering optics[M]. Beijing: Machine Press, 2009:2-3.
郁道银, 谈恒英. 工程光学[M]. 北京: 机械工业出版社, 2009:2-3.
[2] Mu Da, Liu Zhiying. Optical measurement[M]. Jilin: Changchun University of Science and Technology Press, 2011:23-28.
牟达, 刘智颖. 光学测量[M]. 吉林: 长春理工大学出版社, 2011:23-28.
[3] Song Kefei, Mi Baoyong. Computerized photo-electric automatic refractometer with high accuracy[J]. Chinese Journal of Scientific Instrument, 2005, 26(11): 1159-1162.
宋克飞, 米宝永. 计算机控制的高精度光电折射仪[J]. 仪器仪表学报, 2005, 26(11): 1159-1162.
[4] Pereira M B, Horowitz F. Direct near-surface measurement of refractive index: extension of the Brewster-pfund method to graded-index films[J]. SPIE, 2003, 4829: 278-279.
[5] Hori Y, Hirai A, Minoshima K. Quadrature detection and cancellation of absolute wavelength in a prism-pair interferometer for high-accuracy refractive index measurements of glasses[J]. Lasers and Electro-Optics, 2009, 1(2):2-4.
[6] Ni Lei, Ren Qifeng, Liao Sheng. Measurement of cryogenic refractive index of IR materials: uncertainty analysis[J]. Opto-Electronic Engineering, 2010, 37(10): 77-82.
倪磊, 任栖锋, 廖胜. 红外材料低温折射率测定: 不确定度分析[J]. 光电工程, 2010, 37(10): 77-82.
[7] Huang Fuquan, Lu Shanying, Wang Shaomin. The refractive index measurement of high refractive index glass beads[J]. Acta Photonica Sinica, 2001, 30(6): 753-756.
黄富泉, 卢山鹰, 王绍民. 高折射率玻璃微珠折射率的测量[J].光子学报, 2001, 30(6): 753-756.
[8] Ma Botao, Pei Chunyan, Li Xiaochun. Modified formula of environment conditions in precision measurement of optical glass refractive index[J]. Journal of Applied Optics, 2012, 33(5), 936-939.
马伯涛, 裴春艳, 李小春. 光学玻璃折射率精密测量中环境条件修正公式的研究[J]. 应用光学, 2012, 33(5), 936-939.
[9] Takeyama N, Matsuhara H, Maeda L, et al. Measurement of refractive indices of 20 optical materials at low temperatures[J]. Optical Engineering, 2006, 45(8):083401.
[10] Owens J C. Optical refractive index of air: dependence on pressure, temperature and compossition[J]. Applied Optics, 1967, 6(1): 51-59.
[11] Ji Xiaohui, Chen Tong. Measuring refractive index of optical glass based on photo-electric technology[J]. Journal of Applied Optics, 2010, 31(5): 778-780.
纪小辉, 陈彤. 基于光电技术的玻璃折射率测量[J]. 应用光学, 2010, 31(5): 778-780.
[12] LI Jianshe. To improve the measurement of the brewster angle and the refractive index of the glass by using CCD and spectrometer[C]. CDEE, 2010, 95: 410-412
[13] Hori Y, Hirai A, Minoshima K, et al. High-accuracy interferometer with a prism pair for measurement of the absolute refractive index of glass[J]. Appl Opt., 2009, 48(11): 2045-2050.
