多平面全息三维显示及其噪声消除研究

周鹏程，毕 勇，孙敏远，亓 岩，张仁栗

(1.中国科学院大学，北京 100049; 2.中国科学院 光电研究院，北京 100094)

引言

全息三维显示能够完美再现自然界的光波信息，提供人眼全部的深度要素，产生来自于真实自然场景的立体视觉，因此被公认为最具前景的3D显示技术[1-2]。全息显示应用领域极其宽广，涵盖军事、医疗、工业、商业、教学、科研、影视、娱乐等各个领域，一旦全息显示技术步入应用，将会引发各行业的产业升级，其潜在市场规模极为巨大。

全息显示最早是1948年，由D. Gabor在电子显微镜的研究中发现和提出，采用胶片记录经物体衍射未聚焦的光学波前，得到全息图，然后以相干光照明全息图，再现出原物体的放大的光学像[3]。1967年Lohmann等人提出计算全息技术[4-5]，使用计算机产生全息图，不必进行实际的光学记录过程，并可以再现虚拟的物体光学图像。近年来随着光电子器件的发展，以空间光调制器(spatial light modulator, SLM)为代表的全息显示设备能够方便快捷地加载计算全息图，实现动态乃至于实时的激光全息显示，因而吸引了国际著名研究机构和跨国公司的广泛关注[6]，成为全球研究热点之一。

基于计算全息和SLM的动态全息显示技术，通过计算机产生计算全息图(computer-generated hologram, CGH)，然后将CGH加载到SLM上，并经过准直的激光照射，即可产生预先设定好的物体的3D图像。现有的SLM种类很多，按光调制方式分类有振幅型、振幅-位相型和纯位相型，其中纯位相型由于不阻碍光的传输，能量利用率高而被广泛使用。纯位相型SLM需要加载的全息图为纯位相型全息图，也称相息图。纯位相型CGH的计算方式分为解析法[7]和迭代法，其中解析法方便快捷，但是产生的3D图像像质差；而迭代法虽然计算量大，但能够产生高清的3D图像。迭代算法包括模拟退火法，基因算法，GS(Gerchberg-Saxton)算法[8]等等,其中GS算法由于收敛速度快，效果好而被广泛使用。

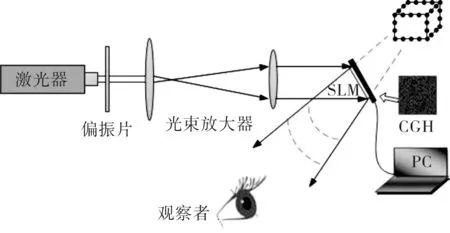
图1 基于计算全息和SLM的三维全息显示原理示意图Fig.1 Schematic diagram of 3D holographic display based on computer holography and SLM

最原始的GS算法仅能再现一个平面，为了获取3D再现图像，三维GS算法被提出。在三维GS算法中，一个3D物体先沿纵向被离散成多个平面(层析法)，并计算得到相应的CGH，然后再现出这些物平面，从而实现3D全息显示。

SLM能够准确、快速、方便地再现出光学波前，因而被广泛使用，但是它的光学结构会产生作为噪声的多级衍射像，严重影响显示效果。如图2(a)，所示，横向上，SLM由像素和像素间隙构成，两者的组成结构是“栅格”结构，在光学效果上，会产生二维光栅效应，将原来的一个图像变为多级衍射像，不仅影响显示，还降低了能量利用效率。具体的多级衍射像效果如图2(b)所示，图中列出了x、y方向±1、±2级的衍射像。

图2 SLM的“栅格”结构和基于SLM的3D显示中的多级衍射像噪声Fig.2 Grid-structure of SLM and noise of multi-order diffraction images in 3D display based on SLM

1 基于GS迭代算法的多平面三维全息显示

1.1 GS算法原理

GS算法是迭代算法，它与解析方法计算全息图的区别在于，解析法通过衍射公式直接计算物体发射的光在全息图平面的光波波前，而GS算法在物体平面和全息图平面之间构建了迭代循环，并在循环中通过振幅替换不断优化全息图，获得能够再现出更接近目标图像的全息图。其流程图如图3所示。光的传播使用傅里叶变换来模拟，振幅替换过程中用目标图像的振幅分布T来取代计算得到的振幅分布F。

但是传统的二维GS算法只能输出一个平面，对于多平面物体，需要用到三维GS算法。如图4所示，三维GS中，物光的传播使用菲涅尔衍射公式来模拟，而不是二维GS算法中的傅里叶变换，当循环来到某个平面时，振幅替换被执行。

迭代过程涉及的光传播可通过菲涅尔公式模拟：

(1)

式中：U0和Ud分别是近场和远场的复振幅，反映在图4中，分别代表全息面和物平面的复振幅。而在计算机中，这一公式可转换为傅里叶变换形式，并可使用快速傅里叶变换算法来加速计算[9]：

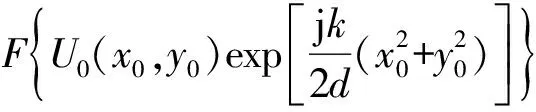
(2)

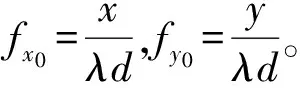
以2个平面构成的物体为例，具体的三维GS的算法程序如下：

1) 开始。全息图平面，全息面的位相是随机位相，振幅为全平面，等于1。

2) 传播。全息面→平面1，使用菲涅尔衍射公式计算平面1的复振幅。

3) 平面1的振幅替换。步骤2)计算得到的复振幅中，保留相位，其振幅被其目标振幅T1替换。

4) 逆传播。平面1→全息面，使用菲涅尔衍射公式的逆形式，计算全息面的复振幅。

5) 全息面的振幅替换。保留计算得到的位相，将振幅设为全平面，等于1。

6) 传播。全息面→平面2，使用菲涅尔衍射公式计算平面2的复振幅。

7) 平面2的振幅替换。程序步骤4) 中计算得到的复振幅中，保留相位，其振幅被其目标振幅T2替换。

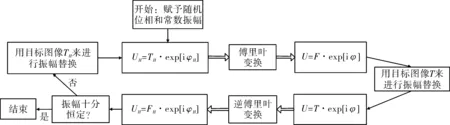
图3 二维GS算法流程图Fig.3 Flow chart of 2D GS algorithm

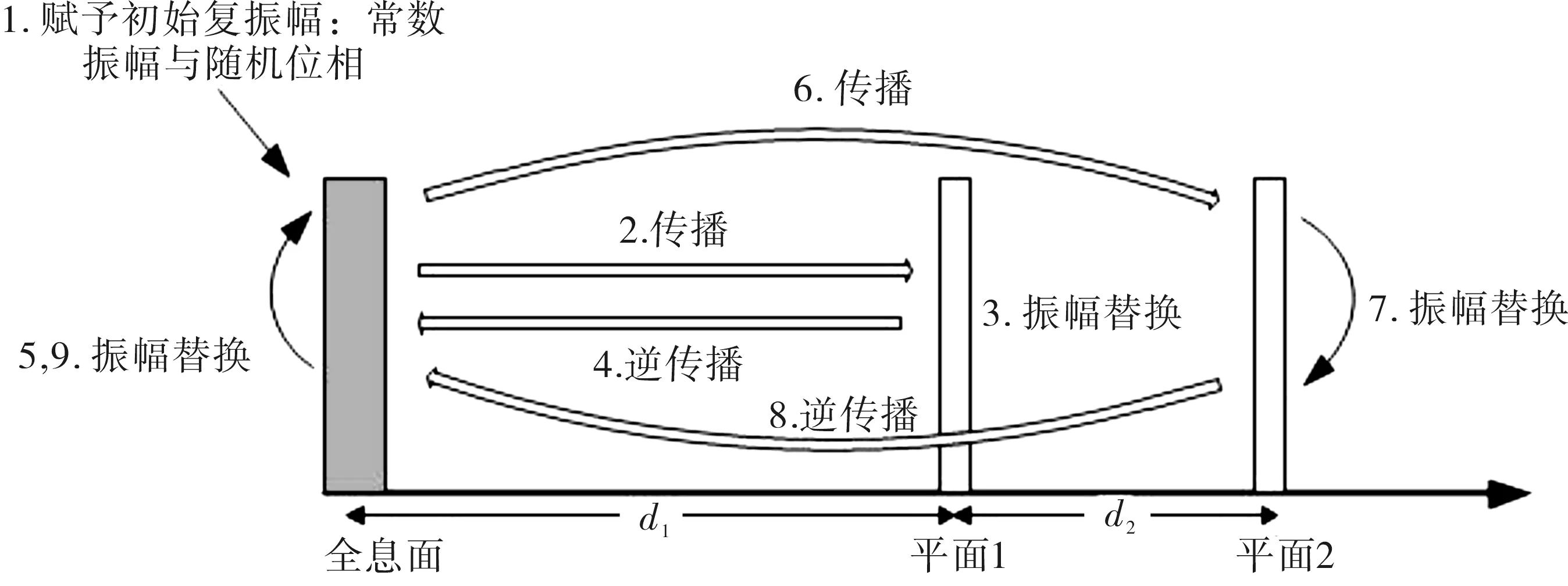
图4 三维GS算法原理示意图Fig.4 Schematic diagram of 3D GS algorithm

8) 逆传播。平面2→全息面，使用菲涅尔衍射公式的逆形式，计算全息面的复振幅。

9) 全息面的振幅替换。保留计算得到的位相，将振幅设为全平面，等于1。

10) 重复步骤2)～9)。

循环可以通过设定循环数来控制何时停止，也可以设定如图3所示的条件来控制何时停止。当循环停止后，将所得全息面的位相值经过求余后，得到灰度值，编写成一个全息图，作为SLM的输入信号。求余操作如下：

H(m,n)=mod[φ0(m,n),2π]

(3)

式中：φ0为全息面位相，-M/2≤m≤M/2-1,-N/2≤n≤N/2-1；M、N分别为全息图在x、y方向上的像素总数。

1.2 光学仿真与实验结果

为了获得3D图像，我们进行了Matlab平台上的光学仿真，和基于SLM的光学实验。光学仿真中，为了将问题简单化，使用了2个平面构成的3D物体，但足以说明所有的基本问题。全息面到平面1距离d1为200 mm，平面1到平面2距离d2为60 mm，工作波长为532 nm。平面1和平面2所要再现的目标图像如图5所示，分辨率都为1 920像素×1 080像素。全息面和2个物平面的取样点数都为1 920×1 080，但是取样间距不同，全息面取样间距为8 μm×8 μm，2个物平面的取样间距需要进行计算。由于我们使用了(2)式所示的菲涅尔公式的傅里叶解析形式，物平面取样间距可计算如下[11]：

图5 目标图像Fig.5 Target images

(4)

式中：Δx0、Δy0为全息面x、y方向取样间距；Δxd、Δyd是距离全息面为d的物面的取样间距；M、N是x、y方向的取样数。光学实验所用的SLM型号为Holoeye公司PLUTO纯相位SLM，分辨率1 920像素×1 080像素，像元尺寸8 μm×8 μm，开口率为87%，用到的激光波长为532 nm。仿真模拟结果和光学实验结果如图6和图7所示。

图6 数值模拟的再现结果Fig.6 Reconstruction results of numerical simulation

图7 光学实验的再现结果Fig.7 Reconstruction results in optical experiment

本文对灰度图像进行再现，而不是使用如图2(b)那样的黑白图像。这具有很大的困难。因为灰度图像的信息量大，再现难度高，国内外研究者绝大多数都使用黑白图像。而本文中，灰度图像的数值结果与实验结果都很清晰，这解决了灰度图像的再现难题。这一结果归功于GS算法的高精度，它能够获得解析算法难以达到的再现清晰度。

值得注意的是，实验结果与数值结果相比，图像纵横比发生了变化，这与物平面的非均匀取样有关。由(3)式得到图像纵横比与其在x、y方向取样间距密切相关：

(5)

反比于全息面取样间距之比，本文中Lx∶Ly=1,所以实验结果中图像为正方形。

除了以上的二平面物体，我们还构建了由100个平面构成的立方体，并完成了其全息显示，光学实验结果如图8所示。本文中，图7和图8的3D图像都是实像，由屏幕承接而得，这样方便记录。

图8 100个平面构成的立方体的再现图像Fig.8 Reconstruction image of a cubic made of 100 planes

对于实际的3D显示，我们可以使用虚像，具体的做法是对计算得到的全息面复振幅取共轭，这样得到的3D图像立体感更强。

2 平移位相函数消除多级衍射像噪声

2.1 栅格效应对再现像的影响

在图7和图8中，观察到的不是单独的3D图像，而是许多重复的、亮度强弱不一的图像，其产生原因是由于LCOS的栅格结构构成了二维光栅，使入射光发生了光栅衍射效应，产生了多级衍射光[10]。

由(2)式可以得到无栅格效应前的再现像为

U(x,y)=P1·F{U0(x0，y0)·P2}

(6)

P1和P2对应着(2)式中的复振幅项。引入栅格效应后，又引入一个复振幅项P3，则再现像为

Ug(x,y)=P1·F{U0(x0,y0)·P2·P3}=

P1·F{U0(x0,y0)·P2}⊗F(P3)=

U(x,y)⊗F(P3)

(7)

式中：⊗表示卷积；P3是光栅的透过率函数，这里不考虑光栅口径的影响，于是有：

(8)

式中：a是光栅周期，对于SLM等于像素尺寸；a0是开口大小；a0/a是SLM的开口率，则有：

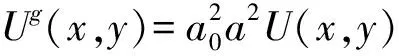
(9)

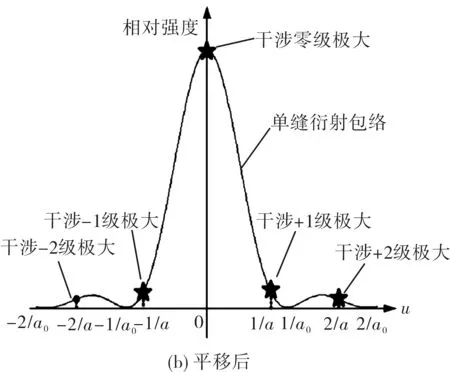
图9 SLM再现像强度分布Fig.9 Intensity distribution of reconstruction image

2.2 多级衍射像的削弱

在光学再现像中，虽然有多级衍射再现像，但是±1级衍射像能量占据了绝大多数，其他级次能量微不足道。但是±1图像分散成了4个图像，能量分散了，而且也不利于显示。如果对再现像位置进行平移，使之占据零级干涉极大，能量将集中于中央位置，以提高能量利用率。平移后强度分布如图9(b)所示。

要在像空间产生平移，根据傅里叶变换位移定律，只需全息面进行相移[11]即可：

(10)

(11)

因此，全息面的相移量为

φs(m,n)=πm+πn

(12)

则全息面上的位相分布为

H(m,n)=mod[φ0(m,n)+φs(m,n),2π]=mod[φ0(m,n)+π(m+n),2π]

(13)

在图8立方体对应的全息图中附加相移函数，产生新的全息图，并加载于SLM上，光学实验结果如图10所示。

图10 多级衍射像噪声的削弱Fig.10 Elimination of multi-order diffraction images

再现图像由原来的4个较亮的图像变为一个非常亮的图像，图像的亮度大为提高，能量效率大幅度提高。具体的x、y都施加平移时，平移前后光强之比为

(14)

式中a0/a是SLM的开口率，对于Holoeye PLUTO SLM,该值为87%，则前后光强比为0.263 6∶1，平移后零级能量是之前1级像能量的379%。

3 结论

动态激光全息三维显示技术具备全视差，完全再现自然光波信息的优点，相对于市场上其他3D显示技术而言，全息3D显示技术在基本物理原理上具备无可比拟的优越性，是最有发展前景的3D技术。本文基于层析法和GS算法，计算了多平面物体的全息图，获得了灰度图像的清晰再现像，产生了由100个平面构成的立方体的3D图像。在此基础上，本文使用位相平移函数，实现了再现像平面的图像平移，将多个级次的衍射像变为单个零级衍射像，能量利用率提升到原来的379 %，多级衍射像噪声被大幅度削弱。接下来，我们将对基于GS算法的全息图计算的加速开展研究，以期获得高速动态全息显示。

[1] Yang Guijuan, Mei Yan, Bai Yaxiang, Development and application of holography[J]. Journal of Applied Optics, 2006,27(2): 96-100.

杨桂娟, 梅妍, 白亚乡. 全息术及其应用[J]. 应用光学,2006,27(2): 96-100.

[2] Huebschman M, Munjuluri B, Gamer H. Dynamic holographic 3-D image projection[J]. Optics Express,2003,11: 437-445.

[3] Gabor D. A new microscopic principle[J]. Nature,1948,161: 777-778.

[4] Lohmann A W，Pairs D. Binary Fraunhofer holograms, generated by computer[J]. Applied Optics,1967,6(1): 1739-1748.

[5] Yu Zuliang, Jin Guofan, Computer-generated hologram[M]. Beijing: Tsinghua University Press, 1984.

虞祖良，金国藩. 计算机制全息图[M].北京: 清华大学出版社, 1984.

[6] Shimobaba T, Nakayama H, Masuda N, et al. Rapid calculation algorithm of Fresnel computer-generated-hologram using look-up table and wavefront-recording plane methods for three-dimensional display[J]. Optics Express,2010,18: 19504-19509.

[7] Yang Maotian，Ding Jianping. Area encoding for design of phase-only computer-generated holograms[J]. Optics Communications,2002,203: 51-60.

[8] Gerchberg R W，Saxton W O. A practical algorithm for the determination of phase from image and diffraction plane pictures[J]. Optik,1972,35: 237-246.

[9] Li Junchang，Xiong Bingheng. Tutorials of information optics [M]. Beijing: Science Press, 2011.

李俊昌，熊秉衡，信息光学教程[M].北京：科学出版社，2011.

[10] Yu Yingjie, Wang Tao, Zheng Huadong. Optimization of optoelectronic reconstruction of phase hologram by use of digital blazed grating[J]. Acta Physics Sinica, 2009,58: 3154-3160

于瀛洁, 王涛, 郑华东. 基于数字闪耀光栅的位相全息图光电再现优化[J]. 物理学报,2009,58: 3154-3160.

[11] Goodman J W. Introduction to Fourier optics[M]. USA: Roberts and Company Publishers, 2005.