土水特征曲线形状对降雨条件下土质边坡稳定性的影响研究

薛海斌，党发宁，尹小涛，杨超，周晓平

(1.西安理工大学 岩土工程研究所，陕西 西安 710048；2.中国科学院武汉岩土力学研究所岩土力学与工程国家重点实验室，武汉 430071；3.中国水电顾问集团西北勘测设计研究院，陕西 西安 710065)

土水特征曲线反映了土的湿度指标(体积含水率、重量含水量、饱和度)与吸力之间的关系，是非饱和土特性研究中最重要的物理力学参数。根据土水特征曲线,结合饱和渗透系数和渗透系数模型,确定非饱和渗透系数函数，通过现场测量的基质吸力分布换算体积含水率的时空分布，也可以间接地反映土体的孔隙大小分布状况，更重要的是可以确定非饱和土的强度。然而土水特征曲线的测定周期长，并且测量过程中影响因素众多[1]，这给非饱和土的物理力学特性研究带来了诸多不便，于是运用数值方法研究土水特征曲线形状对非饱和土边坡渗流场及稳定性的影响具有重要的理论意义。

目前，土水特征曲线形状对非饱和土边坡渗流场与稳定性的影响研究方面的成果甚少。吴礼舟、黄润秋基于一维Richards方程，采用差分法研究了V-G模型中各参数对非饱和土渗流分析的影响[2]。沈梦芬、谭晓慧等运用正交试验设计方法研究了边坡稳定性对膨胀土土水特征曲线拟合参数a、n和m的敏感性[3]。吴国雄、王力等研究了粘土、粉土和砂土3种土水特征曲线对库水位升降作用下的非饱和土边坡稳定性的影响[4-5]。以上成果中，均指出土水特征曲线对非饱和土边坡渗流与稳定分析至关重要，但很少有成果系统地研究土水特征曲线的各控制参数对非饱和土质边坡渗流场及稳定性的影响。

用于描述土水特征曲线模型中的参数可分为两类：①与体积含水率或者基质吸力相关的特征点(如饱和体积含水率、残余体积含水率和进气压力值)；②经验性或半经验性拟合常数，这些常数用于拟合特征点之间曲线的形状。不同的土水特征曲线模型中所采用的拟合常数与土体的物理特性如孔径分布、进气压力值等相关，按照拟合常数的个数不同，模型之间可产生很大的差异。其中典型的数学模型有Brooks-Corey模型、Van-Genuchten模型和Fredlund-Xing模型。与B-C模型相比较，V-G模型的吸力范围较广、能更好地拟合实际的土水特征曲线的形状，能更有效地表征在进气值和趋近残余含水率状态时的平滑过渡情况，因此得到了广泛应用。本文研究V-G模型中的各个参数对边坡渗流场与稳定性的影响。

1 基于基质吸力的非饱和土抗剪强度理论

1980年，Van Genuchten[6]通过对土水特征曲线的研究，得到非饱和土体体积含水率与基质吸力之间的幂函数形式的关系式：

(1)

式中,Θ为标准化体积含水率，Se称为有效饱和度，θr为残余体积含水率，θs为饱和体积含水率，a、n、m为拟合参数，其中a约等于进气压力值，n与土的孔径分布有关，m与土水特征曲线的整体对称性有关，常与n具有关系:m=1-1/n，ψ为待求的基质吸力。

Van Genuchten(1980)将式(1)代入Burdine(1953)与Mualem(1978)提出的统计传导率模型中，得到非饱和土渗透系数函数(式(2))[7]：

(2)

式中,ks为饱和渗透系数。

从上述方程可以看出，只要饱和渗透系数和拟合参数a、m知道了，非饱和渗透系数函数就可以预测出来。

然而要想进行降雨条件下非饱和土边坡的稳定性分析，必须在上述非饱和参数的基础上，引入非饱和土抗剪强度理论，目前岩土工程界普遍认可的非饱和土抗剪强度理论是Fredlund等提出的基于双应力变量(σ-ua)和(ua-uw)的非饱和土抗剪强度公式[8]：

τf=c′+(σ-ua)tanφ′+(ua-uw)tanφb

(3)

(4)

将V-G模型式(1)代入式(4),可得基于基质吸力的非饱和土抗剪强度公式：

(5)

本文以上述公式为理论基础,应用Morgenstern-Price法对边坡进行了稳定性分析。

2 研究方案

为了研究以上V-G模型中各参数对降雨条件下非饱和土边坡渗流与稳定性的影响，通过Geostudio软件控制其它参数不变，改变单一因素来研究其对边坡渗流场和稳定性的影响。

2.1 计算模型

为了研究问题的方便，选取理想的土质边坡(见图1)。图中，B-E为初始地下水位线，O-O为观测断面，O-O线与坡面BC的交点为观测点，坐标为(28.55，30)。计算模型共划分出14 935个节点，14 791个单元。

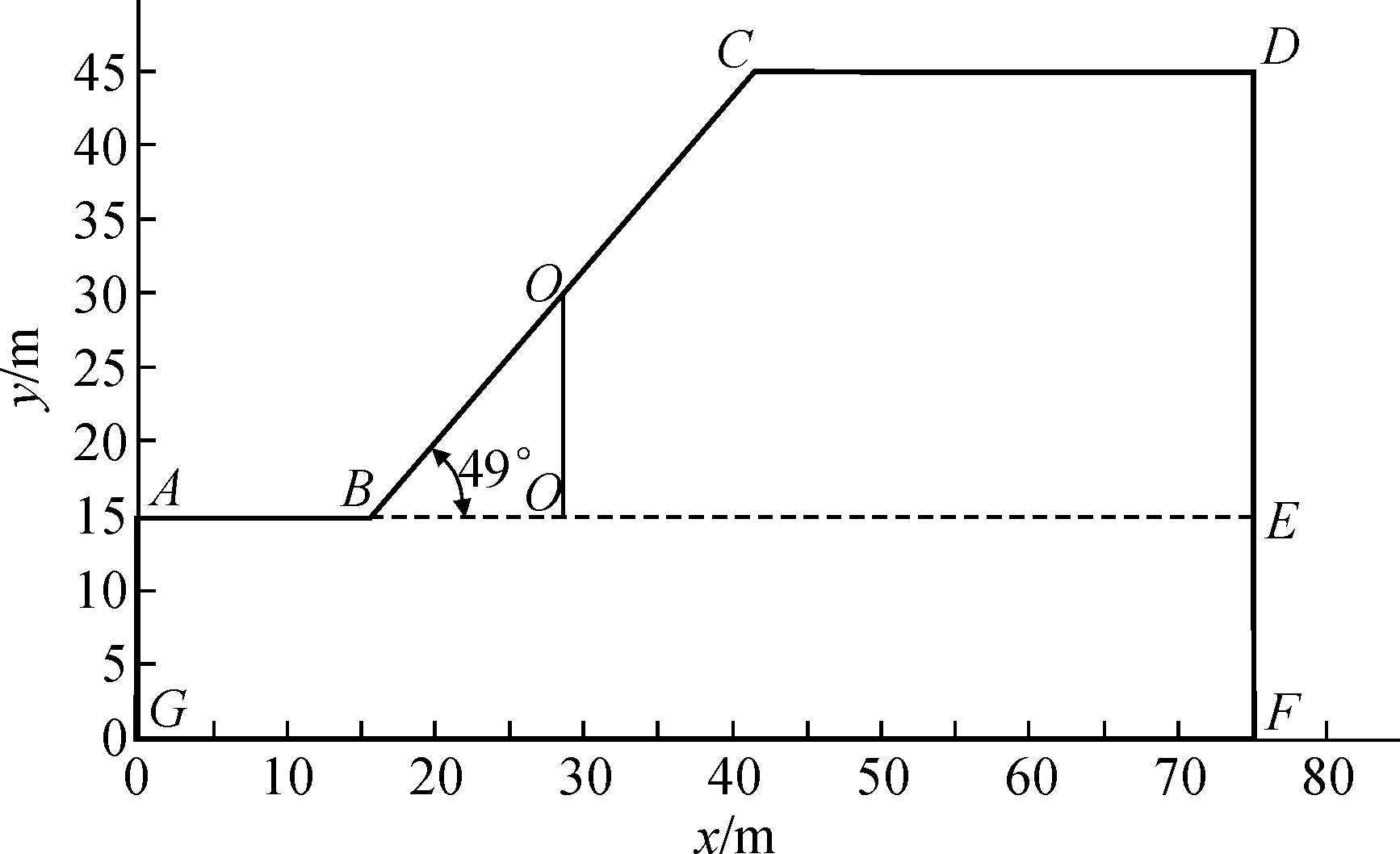
图1 计算模型图

2.2 计算边界条件

计算模型中ABCD为降雨入渗边界，同时也为自由出渗边界，降雨过程中根据渗透系数与降雨强度之间的相互关系决定ABCD为入渗边界还是水头边界，如果渗透系数大于降雨强度，则ABCD为入渗边界，反之，则ABCD为水头边界；AGFD为不透水边界。

2.3 计算初始条件

计算中的初始条件如图2所示，最大基质吸力为80 kPa。

图2 初始孔隙水压力分布等值线图

2.4 材料参数的选取

标准工况下的土水特征曲线使用V-G模型：a=20 kPa，n=2，m=1-1/n=0.5，θs=0.46，θr=0.08[9-13]。渗透系数函数由土水特征曲线和饱和渗透系数依据公式(2)求出。

非饱和抗剪强度公式采用式(5)的表达式，其它物理力学参数[14]为：天然密度1 600 kg/m3, 干密度1 430 kg/m3, 饱和渗透系数5×10-6m/s, 有效粘聚力20 kPa, 有效内摩擦角30°。

2.5 降雨参数的选取

降雨与计算的相关参数为：降雨强度4.167 mm/h, 降雨历时960 h, 计算时间1 920 h。

2.6 计算方案

为了进行单因素的敏感性分析，控制其它参数不变，分别选取a、n和θr的三种不同值，来研究其对边坡渗流场及稳定性分析的影响，具体计算方案如表1所示。

表1 V-G模型中参数敏感性分析的方案设计

各方案对应的土水特征曲线和渗透系数函数如图3～图8所示。

图3 不同a值的土水特征曲线(方案一)

图4 不同a值的渗透系数函数(方案一)

图5 不同n值的土水特征曲线(方案二)

图6 不同n值的渗透系数函数(方案二)

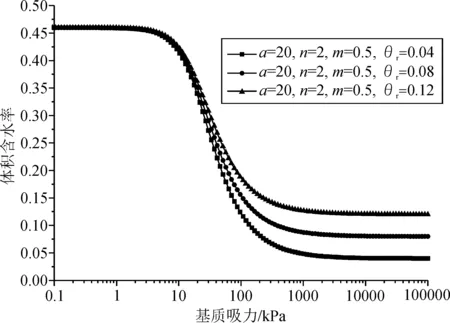
图7 不同θr时的土水特征曲线(方案三)

图8 不同θr时的渗透系数函数(方案三)

3 V-G模型中各参数对非饱和土边坡稳定性的影响分析

3.1 进气值a对非饱和土边坡稳定性的影响分析

在边坡内部保持相同初始基质吸力分布的条件下，随着进气值a值的增大，土水特征曲线右移,意味着边坡体内的初始体积含水率提高，在非饱和土中，水通过充满水的孔隙空间流动，所以体积含水率高将导致边坡体内的水流速度加快，于是边坡内地下水位线的上升和下降速率增大，如图9所示。

图9 不同a值在降雨结束时刻和降雨停止后960 h的地下水位线

降雨过程中，随着进气值a值的增大，湿润锋的前进速率增大，O-O断面处地下水位的上升速度增大，基质吸力减小，体积含水率有所提高，各点达到稳定体积含水率的时间减小，并且稳定体积含水率的数值增大，当停止降雨后，进气值a值越大，土的持水能力越强，导致体积含水率减小得越慢，如图10～图11所示。

图10 不同a值时O-O观测断面的孔隙水压力随高程变化曲线

图11 不同a值时O-O观测断面的体积含水率随高程的变化曲线

由于a值的变化导致边坡内部的初始体积含水率不同，进而导致边坡初始安全系数不同。如果初始安全系数不同，那么分析a值对安全系数的影响就不具有对比意义了，因此采用标准化的安全系数来研究a值对安全系数的影响，其中标准化的安全系数即任一时刻的安全系数与开始时刻的安全系数的比值。

从图12标准化的安全系数与时间的关系曲线可以看出,随着a值的增大，在降雨过程中边坡安全系数的降低速率增大，停止降雨后安全系数的回升速率也在增大。

图12 不同a值时标准化安全系数随时间的变化过程线

究其原因可以归结为:进气值a值的增大意味着体积含水率的增大，体积含水率的增大意味着水流动速率的增大。从渗透系数函数可以看出进气值a值的增大意味着渗透系数的增大，因此水的入渗速率增大，最终导致安全系数的变化速率加大。

3.2 孔径分布相关系数n对非饱和土边坡稳定性的影响分析

随着n值的增大，土体的土水特征曲线中间段斜率变陡，在边坡内部保持相同初始基质吸力分布的条件下，初始体积含水率降低，低的体积含水率意味着水的运动速率小，于是导致地下水位线的上升速率减小。

在停止降雨后，n值越大，其保持水分的能力相应降低，排水速率增大，地下水位线的下降速率增大，如图13所示。

图13 不同n值在降雨结束时刻和降雨停止后960 h的地下水位线

在降雨过程中，随着n值的减小，O-O观测断面上湿润锋的前进速率在增大，O-O观测断面处地下水位的上升速率增大，基质吸力减小，体积含水率提高，各点达到稳定体积含水率的时间减小，并且稳定体积含水率的数值在增大，当停止降雨后，随着n值的减小，表层土体的排水能力减弱，如图14～图15所示。

图14 不同n值时O-O观测断面的孔隙水压力随高程的变化曲线

图15 不同n值时O-O观测断面的体积含水率随高程的变化曲线

随着n值的增大，在降雨过程中安全系数的降低速率有所减小，降雨结束后安全系数的回升速率也有所减小，如图16所示。究其原因可以归结为：n值的大小影响着土水特征曲线的斜率，n值越高表示土水特征曲线越陡，保持相同初始基质吸力的条件下，低于进气值时，n值越高，体积含水率越高；高于进气值以后，n值越高，体积含水率越低。

因此降雨情况下边坡的安全系数变化主要受初始吸力控制，主要看初始吸力是高于还是低于进气值，本次分析由于初始吸力高于进气值，因此随着n值的增大，土体的体积含水率降低，入渗速率减小，排水速率增大，导致安全系数在降雨过程中的降低速率减小，降雨结束后安全系数的回升速率也有所减小。

图16 不同n值时标准化安全系数随时间的变化过程线

3.3 残余含水率θr对非饱和土边坡稳定性的影响分析

随着残余含水率θr的增大，土体的土水特征曲线上移，在边坡内部保持相同初始基质吸力分布的条件下，意味着边坡内土体的体积含水率有所增大。

高的体积含水率导致水的运动速率增大，所以地下水位线的上升速率增大。

在停止降雨后，残余含水率越大，其保持水分的能力相应越强，排出的水量就越少，地下水位线的下降速率也越小，如图17所示。

图17 对应于不同的残余含水率θr时，在降雨结束时刻和降雨停止后960 h的地下水位线

降雨过程中，随着残余含水率θr的增大，湿润锋的前进速率增大，O-O断面处地下水位的上升速度增大，基质吸力减小，体积含水率有所提高，各点达到稳定体积含水率的时间减小，并且稳定体积含水率的数值在增大。

当停止降雨后，残余含水率θr越大，土的持水能力越强，所以导致体积含水率减小得越慢，如图18～图19所示。

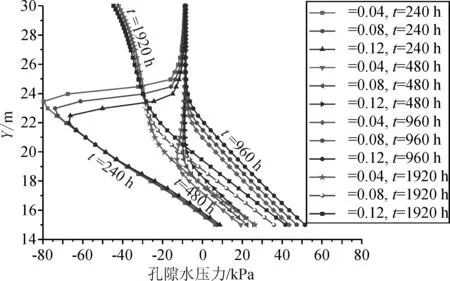
图18 不同残余含水率θr时O-O观测断面的孔隙水压力随高程的变化曲线

图19 不同残余含水率θr时O-O观测断面的体积含水率随高程的变化曲线

随着残余含水率θr的增大，在降雨过程中安全系数的降低速率有所增大，但是降雨结束后安全系数回升达到稳定的时间减小，如图20所示。究其原因可以归结为：在边坡内部保持相同初始基质吸力分布的条件下，残余含水率θr的增大意味着边坡内土体的体积含水率的增大，体积含水率的增大意味着水流动速率的增大，并且从渗透系数函数看出不同残余含水率θr情况下，土体的渗透系数函数相同，所以导致降雨过程中安全系数的降低速率增大，在停止降雨后，由于土体的持水能力随着残余含水率θr的增大而增强，导致排出的水量减小，所以安全系数回升达到稳定的时间减小。

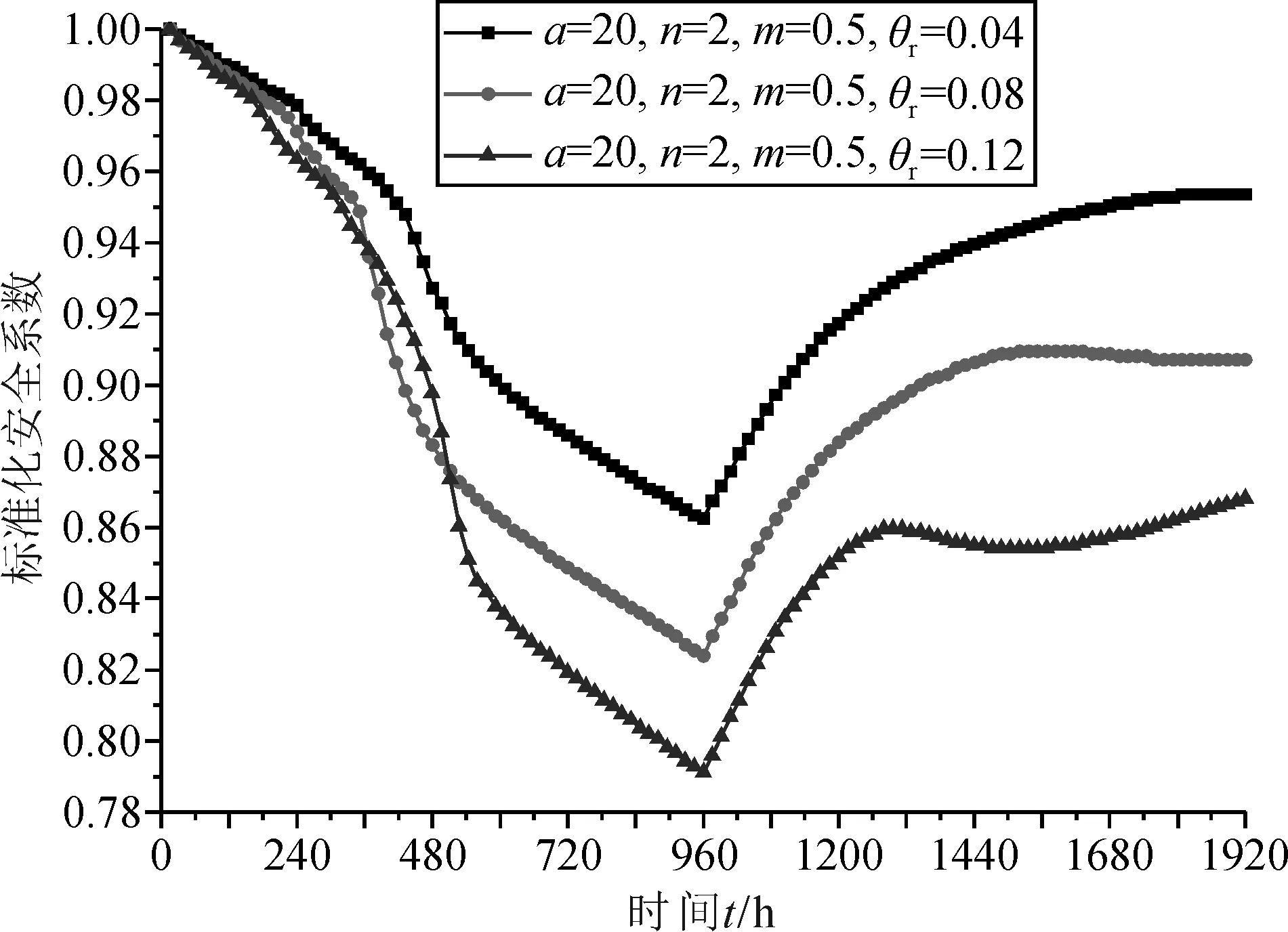
图20 不同残余含水率θr时标准化安全系数随时间的变化过程线

4 结 论

本文运用数值的方法研究了V-G模型中各参数对降雨条件下土质边坡渗流场的影响，进而从机理上解释了这些参数对降雨条件下边坡稳定性的影响，得到如下主要结论。

1)在边坡内部保持相同初始基质吸力分布的条件下，进气值a的增大导致在降雨过程中非饱和土质边坡安全系数降低速率增大，在降雨结束后安全系数的回升速率也增大。

2)在边坡内部保持相同初始基质吸力分布的条件下，低于进气值时，n值的增大导致在降雨过程中安全系数的降低速率增大，在降雨结束后安全系数回升速率也增大；高于进气值时，n值的增大导致在降雨过程中安全系数的降低速率减小，在降雨结束后安全系数回升速率减小，因此降雨情况下，n值对边坡安全系数变化的影响主要受初始吸力控制。

3)在边坡内部保持相同初始基质吸力分布的条件下，残余含水率θr的增大，导致在降雨过程中安全系数的降低速率增大，但是在降雨结束后安全系数回升到稳定的时间减小。

参考文献：

[1] 刘奉银，张昭，周冬,等.影响GCTS土水特征曲线仪试验结果的因素及曲线合理性分析[J]. 西安理工大学学报，2010, 26(3):320-325.

Liu Fengyin, Zhang Zhao, Zhou Dong,et al. Debugging of GCTS-Type SWCC device and analysis of the corresponding technical indexes[J]. Journal of Xi’an University of Technology, 2010, 26(3):320-325.

[2] 吴礼舟，黄润秋.非饱和土渗流及其参数影响的数值分析[J].水文地质工程地质，2011，38(1):94-98.

Wu Lizhou, Huang Runqiu. A numerical analysis of the infiltration and effects in unsaturated soil[J]. Hydrogeology & Engineering Geology, 2011，38(1): 94-98.

[3] 沈梦芬，谭晓慧，李丹,等.降雨入渗下膨胀土边坡的稳定性分析[J].安徽建筑工程学院学报:自然科学版，2012,20(1):66-70.

Shen Mengfen,Tan Xiaohui,Li Dan,et al. Slope stability analysis of expansive soil under rainfall infiltration[J]. Journal of Anhui Institute of Architecture & Industry(Natural Science). 2012,20(1):66-70.

[4] 吴国雄，罗丽娟，陈麟.土水特征曲线对水位下降库岸稳定的影响分析[J].公路，2011，(10)：18-22.

Wu Guoxiong, Luo Lijuan, Chen Lin. Analysis of influence of soil water characteristic curve on bank stability calculation when reservoir water level decreases[J]. Highway, 2011，(10)：18-22.

[5] 王力，王世梅，杨贝贝.库水位变动条件下土-水特征曲线对滑坡稳定性计算结果的影响研究[J].三峡大学学报:自然科学版，2012,34(3)：10-14.

Wang Li, Wang Shimei, Yang Beibei. Research of SWCC on stability calculation of landslides under reservoir water fluctuation [J]. Journal of China Gorges University(Natural Sciences), 2012,34(3)：10-14.

[6] Van Genuchten M TH.A closed-form equation for predicting the hydraulc conductivity of unsaturated soils[J]. Soil Science Society of America Journal,1980，44: 892-898.

[7] Lu Ning, William J Likos著. 非饱和土力学[M].韦昌富，侯龙，简文星,译. 北京：高等教育出版社，2012.

[8] Fredlund D G,Rahardjo H著. 非饱和土土力学[M]. 陈仲颐,译. 北京:中国建筑工业出版社，1997.

[9] 王铁行，卢靖，岳彩坤.考虑温度和密度影响的非饱和黄土土水特征曲线[J].岩土力学，2008，29(1)：1-5.

Wang Tiehang, Lu Jing, Yue Caikun. Soil-water characteristic curve for unsaturated loess considering temperature and density effect[J].Rock and Soil Mechanics, 2008，29(1)：1-5.

[10] 周冬.应力作用下非饱和土土水特征曲线及渗透性研究[D].西安:西安理工大学，2010.

Zhou Dong. Investigation of stress state-dependent soil water characteristic curve and permibility behavior for unsaturated soil[D]. Xi’an:Xi’an University of Technology, 2010.

[11] 刘奉银，张昭,周冬,等.密度和干湿循环对黄土土水特征曲线的影响[J].岩土力学，2011,32(S2)：132-136.

Liu Fengyin, Zhang Zhao, Zhou Dong, et al. Effect of initial density and drying-wetting cycle on soil water characteristic curve of unsaturated loess [J].Rock and Soil Mechanics, 2011,32(S2)：132-136.

[12] 王康.非饱和土壤水流运动及溶质迁移[M].北京：科学出版社，2010

[13] Griffiths D V, Lu N. Unsaturated slope stability analysis with steady infiltration or evaporation using elasto-plastic finite elements[J].International Journal for Numerical and Analytical Methods In Geomechanics,2005,29：249-267.

[14] 刘祖典.黄土力学与工程[M].西安：陕西科学技术出版社，1997.

[15] 黄润秋，戚国庆．非饱和渗流基质吸力对边坡稳定性的影响[J]．工程地质学报，2002，10(4):343-347.

Huang Runqiu，Qi Guoqing. The effect of unsaturated soil suction on slope stability[J]. Journal of Engineering Geology, 2002，10(4):343-347.

[16] 王瑞钢，闫澍旺，邓卫东. 降雨作用下高填土质路堤边坡的渗流稳定分析[J].中国公路学报，2004，17(4): 25-30.

Wang Ruigang, Yan Shuwang, Deng Weidong. Analysis of seepage stability of high-filled embankment slope due to rainfall infiltration[J]. China Journal of Highway and Transport,2004，17(4):25-30．