“水深平均二维数学模型”在跨河桥梁防洪评价壅水计算中的应用
2014-03-26
(扬州市勘测设计研究院有限公司, 江苏 扬州 225100)
1 前 言
跨河桥梁压缩河道,致使桥址上游水流变缓,水流动能转换为势能,使得桥梁上游产生壅水,从而影响河道过水能力,抬高上游局部河道的水位。如桥梁壅水过高,将会对河道行洪排涝产生较大影响,严重的会对防洪安全产生较大危害。因此,《河道管理范围内建设项目防洪评价报告编制导则》(试行)中规定,必需进行壅水分析计算。本文以扬州市文昌东路东延工程中的廖家沟大桥为例,介绍了采用“水深平均二维数学模型”进行壅水分析计算的基本方法和主要步骤。
2 数模计算原理简介
“水深平均二维数学模型”分析法是采用数学模型,模拟得出计算区域中逐节点水位、流速等物理量的分布,并用数学分析的方法建立流体运动的基本方程并进行求解,所得出的结果具有普遍性,各种影响因素清晰可见。
3 工程概况
3.1 廖家沟概况
廖家沟为淮河入江水道下段归江河道之一,工程所在处为万福闸至羊尾巴段,全长12.51km。据现测资料,桥址处河道宽深,河口宽约1100m,中有小岛,主泓位于岛西侧。
3.2 廖家沟大桥设计
主桥外形设计为拱形结构,以小岛为中心对称布置。单侧跨径组合为:27.5+45+50+55+60+55+50+45+27.5=415m,共9孔,矢跨比在1∶6.3左右,则主桥总长830m,共18孔。桥梁下部均采用钻孔灌注桩基础。
3.3 计算水文
根据淮河入江水道的历次规划设计,结合《扬州市城市防洪规划成果》,得出壅水计算的各个工况水位组合,见表1:
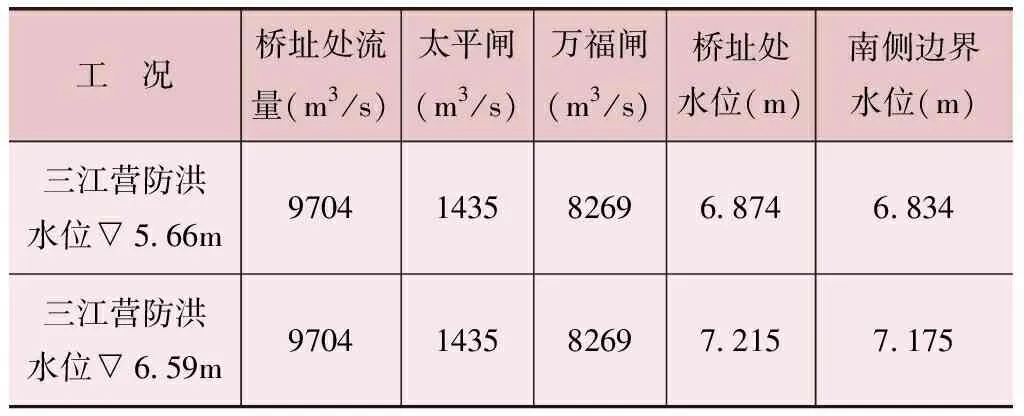
表1 壅水计算工况统计
4 数模分析
4.1 数模分析计算原理
4.1.1 基本方程
数值模拟采用水深平均二维数学模型,模拟得计算区域中逐节点水位、流速等物理量的分布。直角坐标系下的水流运动控制方程组(1)为:连续方程:
运动方程:


式中u,v——水深平均流速沿x,y方向的分量;
h——水位;
H——水深;
γ——运动黏性系数;
g——重力加速度;
C——谢才系数;
n——糙率;
f——地转系数,f=2ωsinφ;
ω——地球自转角速度;
φ——地理纬度。
为易于求解不规则计算区域中的流动问题,将方程组(1)转化成正交曲线坐标系下的水流运动控制方程组(2):
连续方程:
运动方程:
式中u,v的含义为正交曲线坐标系下水深平均流速在曲线坐标ξ,η方向上的分量。
4.1.2 数值求解方法
正交曲线坐标系下的方程组(2)较原直角坐标下的方程组(1)略显复杂,其复杂性主要来自非线性的对流项和扩散项,但变换后的控制方程组各项的物理意义及属性并未改变,黏性项的量级较小,方程组(2)已经忽略了黏性项,所以一般数值方法仍然适用。本项研究采用交替方向隐式法,将一个时步长分作两个时间层,每一层上分别交替改变方向隐式求解连续方程和动量方程。
在计算区域上布置交错网格,除速度布置在次网格中心点外,其余所有变量均布置在主网格中心点上。采用空间中心差、时间前差离散控制方程,控制体积交界面上的物理量由两个相邻节点按线性插值方法求得。
采用ADI法求解方程组(2)的计算格式如图1所示。
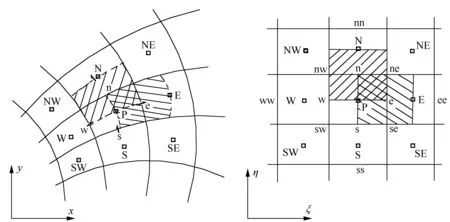
图1 交错网格示意
在时间层nΔt到n+1/2Δt上将连续方程在P节点离散,得:
对运动方程(2b),以节点e为中心离散,并对对流项采用迎风格式处理,可整理得以下代数方程式,即:
同理从时间层(n+1/2)Δt到(n+1)Δt,对连续方程(2a),以节点P为中心离散,整理得代数方程为:
将运动方程(2c)以n点为中心离散,对对流项仍作上风格式处理,可整理得代数方程:
方程(3)~(6)为原基本方程组(2)采用ADI方法的离散方程式,式中各系数Ai,Bi,Ci,Di,(i=1,2,3,4)为网格尺度的函数。
4.1.3 离散方程的求解
将离散方程分别按ξ或η方向联立,则在一个时步长内前后各半时步分别形成满秩方程组。
4.1.4 边界条件、干湿节点的处理方法
上边界采用水位条件,下边界采用流量条件,固壁边界采用不可入条件。
对于因水位变动而引起节点处于干、湿状态不定的问题,采用改进的河床切削法处理。
4.2 计算情况说明
确定计算区域时,东西两岸边界线考虑了计算工况中最高水位可能达到的最大淹没范围。上下游方向,在有枢纽的北侧边界即以枢纽位置作为边界,南侧(下游)以大于1km、并结合考虑地形的实测断面资料予以确定。
计算过程中,以桥址水位与桥址平均比降计算的南部水位边界的水位值作为边界条件。以北侧流量边界和南侧水位边界组合,适当调节河道糙率,使桥址平均水位与已知值基本吻合。河道糙率最终采用范围为0.019~0.021。
4.3 数学模型计算
4.3.1 计算区域
廖家沟计算区域是上起太平闸与万福闸下,向下游取至桥中心线下1.72km,故总计算域长为4.55km。计算网格见图2。

图2 网格计算
4.3.2 计算成果
各工况下上、下游水位及流速计算成果见所附的流速等值线图、流速矢量图、水位等值线图和水位差等值线图。近桥处因受桥墩影响,河道流速、水位等均较紊乱,因此,在各桥墩上、下游取多个节点,列出其水位、流速及水流方向情况。所选节点位置见图3。

图3 廖家沟主泓道节点布置
根据流速等值线图、流速矢量图、水位等值线图和水位差等值线图等计算成果,可直观得出桥梁处河道各处流量、水位、水流方向等,为防洪评价中的雍水、河道河势演变分析等提供理论依据。
本文中列出壅水计算成果见表2,同时附上与壅水计算成果最密切的水位等值线见图4。

表2 廖家沟壅水数模计算成果
5 结 语
从计算结果的图示内容可看出,采用“水深平均二维数学模型”进行壅水分析计算,可得出较精确的壅水计算成果。除水位等值线图外,此方法还可得出流速等值线图和流速矢量图,从而为桥梁建设所带来的河势演变的情况提供较可信、精确的理论分析数据,为得出合理的防洪评价结论提供了有力的技术支撑。
相对于价格昂贵、耗时较长的水工模型试验,“水深平均二维数学模型”计算方法已基本可以满足大多数工程计算的要求,可在防洪评价中进行推广应用。
fffff7
1 陆浩,高冬光.桥梁水力学[M].北京:人民交通出版社,1991.
2 布拉德利.桥梁河道水力学[M].北京:人民交通出版社,1980.
3 王福军.计算流体动力学分析[M].北京:清华大学出版社,2004.
4 齐梅兰.松花江佳木斯河段河工模型试验研究报告[R].1999.
5 陈绪坚,胡春宏.桥渡壅水平面二维数学模型模拟研究[J].中国水利水电科学研究院学报,2003(3):194-200.
6 金忠青.N—S方程的数值解和紊流模型[M].南京:河海大学出版社,1989.
7 周雪漪.计算水力学[M].北京:清华大学出版社,1995.
8 王兴奎.河流动力学[M].北京:科学出版社,2004.
9 王昌杰.河流动力学[M].北京:人民交通出版社,2001.
10 张小峰,等.广东肇庆西江大桥河道平面二维水流模型的研究与应用[C]//卢金友,等.第五届全国泥沙基本理论讨论会论文集.武汉:湖北辞书出版社,2002.
11 张众,经瑞,李洋.豫20线周沈高速公路沙颖河大桥壅水计算[J].治淮,2002(8):38-39.
12 张细兵,余新明,金琨.桥渡壅水对河道水位流场影响二维数值模拟[J].人民长江,2003,34(4):23-24.
13 周建军,林秉南,王连样.河道平面二维水流数值计算[J].水利学报,1991(5):8-18.
