基于CPU/GPU异构平台的全波形反演及其实用化分析

张 猛,王华忠,任浩然,冯 波,隋志强,王延光

(1.同济大学海洋与地球科学学院波现象与反演成像研究组,上海200092；2.中国石油化工股份有限公司胜利油田分公司物探研究院,山东东营257022；3.浙江大学地球科学系,浙江杭州310027)

速度建模是地震偏移成像中的核心问题,高精度的速度建模是地震成像和属性反演的基础。全波形反演(Full waveform inversion,FWI)方法利用整个地震道集的全波形信息进行非线性反演,理论上可以反演出宽波数分布的速度结构。FWI的理论框架于20世纪80年代提出,Tarantola[1]详细给出了FWI的实现框架,提出了基于广义最小二乘反演理论的时间-空间域全波形反演方法。20世纪90年代,Pratt[2]又将其发展到频率-空间域。

FWI虽然在理论上具有严谨的数学物理基础,然而却一直难以得到大规模实际应用,其原因是多方面的。首先,实际地震数据处理中难以提供一个满足FWI要求的初始模型；缺少低频和长偏移距数据,FWI自身也不能给出可靠的初始速度模型。FWI具有强非线性,精度不高的初始速度模型很容易使得FWI陷入局部极小值。其次,实际地震数据的质量也不能满足FWI对数据的要求。噪声和波动方程难以描述的复杂地震波现象极大地干扰了FWI反演,子波的未知和空变增加了反演解的非唯一性。再次,FWI的巨大计算量同样制约着FWI的大规模实际应用。

近年来,高密度宽方位角大偏移距地震采集方式的出现以及CPU/GPU异构计算平台的高速发展,为FWI提供了更好的数据准备以及计算能力支撑。全波形反演或其变种方法有了在实际生产中应用的可能性,成为勘探地球物理界的热点研究课题。由于图形处理器GPU(Graphic Processing Unit)在科学计算中相对CPU的计算效率优势,通过统一计算设备架构平台CUDA(Compute Unified Device Architecture)编写程序可以让GPU执行计算任务,近年来在地球物理领域得到了广泛而成功的应用。如Micikevicius[3]研究了基于GPU的有限差分实现问题,给出了快速实现有限差分的算法。2010年,赵磊等[4]和刘红伟等[5]提出了基于CPU/GPU平台的逆时偏移实现策略。Sun等[6]讨论了TTI介质逆时偏移计算对GPU所面临的挑战。

在数据质量与计算能力得到更大保证的情况下,找到FWI在实际地震资料中的应用方案成为了该理论方法是否实用的关键。近年来,国内外学者分别探讨了多种方案试图使FWI走向实用。当前,比较系统的解决方案主要有:通过修改泛函格式和多尺度反演策略来降低反演解的非唯一性[7]；通过利用特征波场(反射波)来反演宏观背景速度[8]；通过施加各种先验信息和约束条件来降低解空间的大小[9]。

我们从全波形反演理论基础出发,研究并提出了基于CPU/GPU异构平台的时空域声波方程全波形反演算法实现流程。通过理论模型测试证明方法的高精度和高计算效率；同时给出实际地震资料全波形速度反演试处理的初步应用效果。在此基础上进一步讨论分析FWI对实际地震资料质量的要求,针对陆上地震资料的生产性应用提出FWI的实用化策略。

1 全波形反演基本原理

全波形反演方法利用叠前地震波场的运动学和动力学信息重建地下速度结构,具有揭示复杂地质背景下构造与岩性细节信息的潜力。根据实际需要,全波形反演可以在时间、频率、Laplace等域来实现,从计算方法上来看,全波形反演的实现方式主要有梯度导引类方法和牛顿类方法(如高斯-牛顿法)。

以二维声波方程为例,在时间-空间域,声波方程表达为

(1)

利用全波形反演获取地震波速度,一般将全波形反演问题定义为求解目标函数取得极小值时对应的速度,即定义误差泛函:

(2)

式中:p(rg,t;rs)obs和p(rg,t;rs)cal分别为野外观测与数值模拟的地震记录；rs和rg分别表示炮点和检波点坐标；t为时间。全波形反演是通过模拟地震记录与观测地震记录之间的最佳匹配来更新介质速度(或其它参数)的。

时空域波形反演中,通过将剩余波场的反向传播与正向波场进行互相关来计算反问题的负梯度方向,以实现速度更新过程。

2 基于CPU/GPU异构平台的全波形反演算法实现

CPU/GPU异构并行是指采用CPU与GPU协同计算的模式。与CPU集群适合大粗粒度并行不同,GPU计算核心多对细粒度并行的问题更有优势。通常情况CPU负责数据输入与输出以及逻辑判断,并将这些数据拷贝到GPU显存,在GPU进行计算核心计算；然后再将计算结果从显存拷贝回CPU内存,通过CPU输出结果。

全波形反演计算量巨大,应用传统的CPU计算耗时长。综合考虑CPU和GPU计算特点,我们提出了基于CPU/GPU平台的时空域声波方程FWI实现流程(图1)。

图1 基于CPU/GPU平台的时空域声波方程FWI实现流程

分析图1所示实现流程中的计算步骤,其中波动方程正演模拟和梯度计算耗时较长。在每次迭代过程中,求取梯度的部分需要计算两次全波场模拟,而基于单炮的策略容易实现炮的计算机并行。首先,由CPU读取地震子波、速度场和单炮数据,然后,分别将以上数据信息拷贝到GPU显存中,通过输入的子波和速度场进行地震波正演模拟计算。GPU具有超强的计算性能,应用GPU计算全波形反演中的地震波正演模拟和梯度,数据的输入、输出和其它计算由CPU完成。计算结束后,将单炮梯度拷贝回CPU内存,在内存中进行累加,得到总的梯度,最后生成目标梯度函数。

得到梯度和步长以后,速度更新过程按照(3)式执行:

(3)

式中:g为梯度；v为速度；vopt为更新后的速度；αopt为步长。根据(3)式可以实现迭代的速度更新,使梯度导引的反演方法得以实现。当然,还需要设定一个迭代终止的条件,可以为

(4)

(4)式规定了一个迭代收敛的规则,即第n次更新的量小于第n-1次迭代的一定比例,如ε=0.001,则认为迭代收敛,反演可以终止；如果这个条件不满足,则将更新结果作为输入,再进行下一次迭代。

3 理论模型测试与实际资料试处理

3.1 理论模型测试

理论模型测试采用Marmousi速度模型(图2a)。其横向有497个网格,纵向250个网格；横向与纵向网格间距均为12.5m。正演计算采用PML吸收边界。震源子波为10Hz的Ricker子波；炮间距为25m,共200炮；第1炮横坐标为625m。检波器位置固定,每炮437个检波器接收；检波器间距为12.5m；第1炮检波器横坐标为375m。时间步长为1ms；记录长度为4.096s。

用Marmousi模型平滑后的速度模型(图2b)作为反演的初始模型,用梯度方法对该模型进行迭代,不同迭代次数的结果如图3所示。图3给出了迭代次数分别为1次、100次、200次和300次反演得到的速度模型,可以看出经过300次迭代后,反演结果的边界清晰,且速度值收敛到了真实值附近。

图4给出了横坐标分别为3100,4200,5700和6800m处的速度反演结果。可见随着迭代次数的增加,反演的速度曲线与真实模型越来越接近,最终反演结果真实可靠。

图2 Marmousi速度模型(a)及其平滑后的模型(b)

图3 迭代次数为1次(a)、100次(b)、200次(c)和300次(d)的全波形速度反演结果

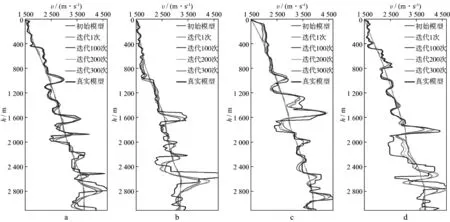
图4 横坐标为3100m(a),4200m(b),5700m(c)和6800m(d)处的速度反演结果垂向对比

进一步对基于CPU程序和基于CPU/GPU异构并行程序进行效率对比测试。针对Marmousi速度模型(点数737,深度采样250,炮数300),基于CPU/GPU平台异构并行计算(1块Fermi2050图形卡)完成一次反演迭代,每次反演相当于3次正演的计算量,300炮迭代1次总共耗时约28min；在CPU平台(双路Xeon X5650,2.67Hz CPU),用MPI实现并行计算,采用主从并行模式,300炮迭代1次总共耗时164min；X5650 CPU 1个核单独进行串行计算时间为1784min。即单块Fermi2050卡相对于单颗X5650 CPU的加速比约为164/28=5.8,相对于X5650 CPU其中一个核的加速比约为1784/28=63.8。

3.2 实际资料试处理

为了检验全波形速度反演解决实际问题的能力,选取胜利油田某工区实际三维地震资料抽取的一条二维线数据进行试处理。该工区陡坡带中西段含油层系多,油藏类型丰富,主要以砂砾岩体油藏为主,油气勘探潜力巨大。

全波形反演中地震子波的估计方法是根据地震直达波到达时与偏移距的关系,首先推算出浅层速度约1740m/s。根据实际地震资料波形,设定选用Ricker子波。通过实验对比确定子波参数:主频20Hz,时延40ms,振幅10000。

图5为通过常规速度分析得到的初始速度模型。图6为经50次迭代后的模拟数据(图6a)与实际观测数据(图6b)的对比,可以看出,模拟数据与观测数据非常接近,基本满足全波形反演需要。

图5 常规速度分析获得的初始速度模型

图6 50次迭代后的模拟炮集(a)和实际观测炮集(b)

图7给出了经过50次迭代反演后最终的速度模型。图8给出了采用图5所示初始速度模型逆时偏移结果(图8a)和全波形反演最终速度模型逆时偏移结果(图8b)。由图8可见,在浅层和大断面处,全波形速度反演速度模型的成像质量较初始速度模型的成像质量有一定的提升,浅层同相轴的连续性明显增强,分辨率有所提高；浅层断层更加清晰,中深层断面信息更加丰富,成像精度有所改进。

但是,由于该二维线并非直接由采集而来,而是从三维数据中抽取得到的。虽然应用全波形反演速度模型进行逆时偏移成像结果的质量有所改进,但这还不足以说明全波形速度反演技术在实际应用中可能达到的应有水平。

图7 经过50次迭代反演后的最终速度模型

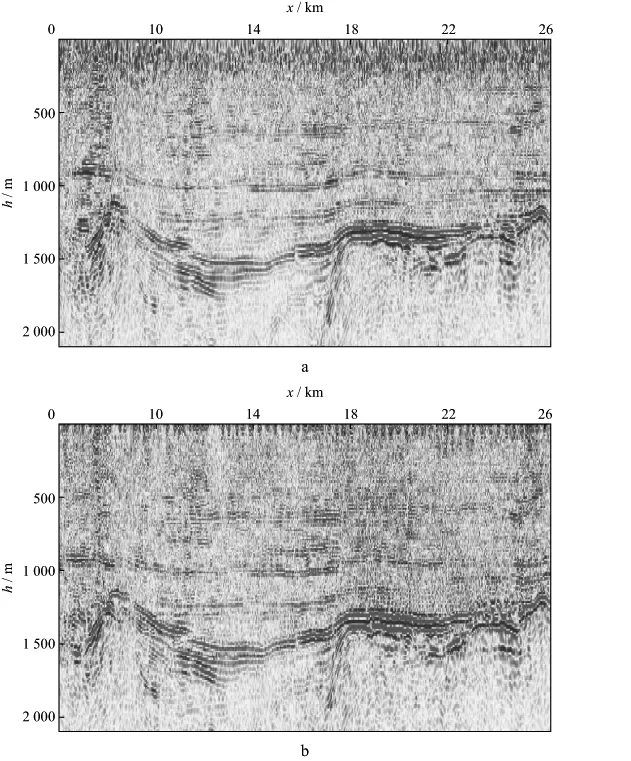
图8 采用图5所示初始速度模型逆时偏移结果(a)和全波形反演速度模型逆时偏移结果(b)

4 FWI在陆上地震资料应用中的问题分析

二维全波形速度反演要取得较好的结果,需要有高质量数据体的支持,具体来说对地震资料有如下要求:测线尽量与构造走向垂直；inline方向偏移距分布丰富,覆盖次数高,含有大偏移距数据；数据空间采样规则,地表高程变化已校正；资料信噪比较高,压制了面波与随机噪声；激发子波能量一致性已校正等。此外,对数据进行子波零相位化整形也是非常重要的。

除了资料因素外,还必须解决的技术问题包括:选择尽可能逼真地描述地震波在地下传播的正演算子(考虑弹性波、吸收衰减和各向异性等)；选择凸性更好的目标反演以及合适的约束条件；建立一个较为精确的初始地球物理模型；构造适当的正则化参数,突出地质和偏移成像的先验信息参与度；重建地震数据中的低频信息。

但是,在陆上实际地震资料采集、处理环节,无论是获得高质量的原始资料还是解决上述技术问题,均存在较大的困难。为了解决这一瓶颈问题,提出如下实现策略和流程:

1) 应用低频大偏移距数据,通过透射波(折射波或回转波)层析,建立宏观背景速度模型,获得低频信息；

2) 应用上述背景速度,通过基于最小二乘的叠前深度偏移获取反射界面信息；

3) 在背景速度和反射界面信息的控制下,通过反射波FWI或者反射波波形层析,获取整个工区的速度信息。

将经典的FWI实现方法拆分为上述技术步骤来实现,降低了FWI的非线性性,这将是FWI走向实用化的重要途径。同时,在具体实现过程中,必须要充分考虑初始模型的先验信息,将多层次、多尺度的多方面信息综合[10],以人机结合的方式进行融合实现。

5 结束语

我们研究并实现了基于CPU/GPU异构平台的全波形速度反演算法。理论数据的测试结果表明,基于Marmousi模型合成数据的全波形速度反演可以反演出高分辨率的速度场；通过GPU加速计算可大幅提高计算效率。进一步对胜利油田某探区实际地震资料进行试处理,取得了初步的应用效果。在此基础上,分析了全波形反演目前在实际应用中存在的问题,提出了全波形反演实用化的策略。

为了使全波形速度反演实用化,需要应用不同的波形信息分步骤进行速度反演,而不是直接利用全波场信息进行反演,这样可以降低经典全波形反演方法的非线性性。同时充分考虑初始模型的先验信息,在实现过程中综合应用多层次、多尺度的多方面信息。只有在满足以上条件时,全波形反演技术才有可能真正解决复杂的实际地质问题。

致谢:感谢中国石油化工股份有限公司胜利油田分公司物探研究院的资助。

参 考 文 献

[1] Tarantola A.Inversion of seismic reflection data in the acoustic approximation[J].Geophysics,1984,49(8):1259-1266

[2] Pratt R G.Seismic waveform inversion in the frequency domain,Part I:theory and verification in a physical scale model[J].Geophysics,1999,64(3):888-901

[3] Micikevicius P.3D finite difference computation on GPUs using CUDA[J].Expanded Abstracts of 78thAnnual Internat SEG Mtg,2008,79-84

[4] 赵磊,王华忠,刘守伟.逆时深度偏移成像方法及其在CPU/GPU 异构平台上的实现[J].岩性油气藏,2010,F06:36-41

Zhao L,Wang H Z,Liu S W.Reverse time migration method and its implementation on CPU/GPU heterogeneous platform[J].Lithologic Reservoirs(in Chinese),2010,F06:36-41

[5] 刘红伟,李博,刘洪,等.地震叠前逆时偏移高阶有限差分算法及GPU实现[J].地球物理学报,2010,53(7):1725-1733

Liu H W,Li B,Liu H,et al.The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation[J].Chinese Journal Geophysics(in Chinese),2010,53(7):1725-1733

[6] Sun X,Suh S.Maximizing throughput for high performance TTI-RTM:from CPU-RTM to GPU-RTM[J].Expanded Abstracts of 81stAnnual Internat SEG Mtg,2011,3179-3183

[7] Shin C,Min D J.Waveform inversion using alogarithmic wavefield[J].Geophysics,2006,71(3):R31-R42

[8] Xu S,Wang D,Chen F,et al.Inversion on reflected seismic wave[J].Expanded Abstracts of 82ndAnnual Internat SEG Mtg,2012,1473-1476

[9] Ma Y,Hale D,Gong B,et al.Image-guided sparse-model full waveform inversion[J].Geophysics,2012,77(4):R189-R198

[10] 杨勤勇,胡光辉,王立歆.全波形反演研究现状及发展趋势[J].石油物探,2014,53(1):77-83

Yang Q Y,Hu G H,Wang L X.Research status and development trend of full waveform inversion[J].Geophysical Prospecting for Petroleum,2014,53(1):77-83