地表温度时空差异对温室效应影响的误差分析

高凤玲， 崔国民， 陶乐仁， 华泽钊

（1.上海理工大学能源与动力工程学院，上海 200093；2.河南科技大学车辆与动力工程学院，洛阳 471039）

自20世纪末以来，温室效应及全球变暖已成为影响气侯变化、人类生存环境和经济发展与安全的重大因素.由于人类生产和社会活动的急剧发展，不断向大气排放CO2，CH4等大量温室气体，致使温室效应增强，这是造成近年来地球变暖的主要原因.根据联合国政府间气候变化专门委员会（IPCC）第4次报告，在过去1906～2005年短短的100年间，近地球表面空气和海洋温度已经升高了0.74±0.18℃［1］.气候学家采用多种气候模型对全球变暖的后果进行预测，如果不能有效地控制CO2的排放，到2100年地球表面温度可能还会继续升高1.1～6.4℃，从而导致灾难性后果［1－2］.但是IPCC气候报告以及大多数有关全球变暖的研究文献在计算中大都只将地表温度处理为单一的平均温度，即认为是288.15K，而实际的地表温度在空间分布上体现出了极大的不均匀性.在不同的时间尺度上，其随昼夜交替、季节变换也会产生不同的变化特点，平均温度的使用，势必使预测结果偏离真实值.鉴于此，笔者在分析全球地表温度时空分布特点的基础上，分别将其作均一化处理并与考虑时间、地域差别之后计算所得到的温室效应进行了比较，预测人为温室气体排放对温室效应的影响.

1 地表温度时空分布特点

地球的能量几乎都来自于太阳的短波辐射，但是受到地球自转与公转、地貌分布特征以及不同纬度大气分布的影响，造成太阳照射到地球的光束能量不可能同时到达地球所有表面，使得地表温度呈现出区域性和时间性的变化特点.表1为根据南北回归线和南北极圈将地球划分的5个气候带及其相应的地表面积（取地球半径为6 371km）和气候模式.其中，考虑到温带和寒带地区四季较大的温差，在时间尺度上又将其均分为夏季与冬季两种气候类型.

从表1可以看出，温带地区的地表面积最大，但也只占了总地表面积的50%，而被大多数文献所采用的288.15K的地表平均温度也仅与温带地区的年平均温度283.2K较为接近，与另外占地50%的热带和寒带的年均温度299.7K和272.2K相比，温差达到了10K以上.在温室效应的计算中，地表辐射通常被简化为黑体辐射［3－4］，按照Stenfan－Boltzmann定律，黑体单位时间内向外辐射的能量与热力学温度的四次方成正比.因此，地表温度每升高1K，将会使其出射能量增加6～8W／m2，10K的温差必将引起地表出射能量的显著改变.而对于温室气体，其选择吸收的特性又会由于地表温度不同造成红外光谱的迁移，从而使得其所吸收的地气系统的长波辐射量发生变化.

表1 地球的气候带与气候模式Tab.1 Climatic zones and climate models of the globe

2 辐射计算的初始条件及假设

IPCC用辐射强迫来衡量某种气体温室效应的大小，即该气体浓度变化后所产生的对流层顶净辐射通量的变化量.由于温室气体主要在大于3μm的红外区有吸收［5］，故只考虑其浓度变化所引起的长波通量的改变，忽略对太阳光的吸收，定义辐射强迫为

式中，LW0，LW1为计算气体取如表2所示工业革命前及当前浓度时，对流层顶部的向上长波通量，W／m2.ΔF越大，说明气体浓度变化后所拦截的红外辐射量越多，温室效应越严重.

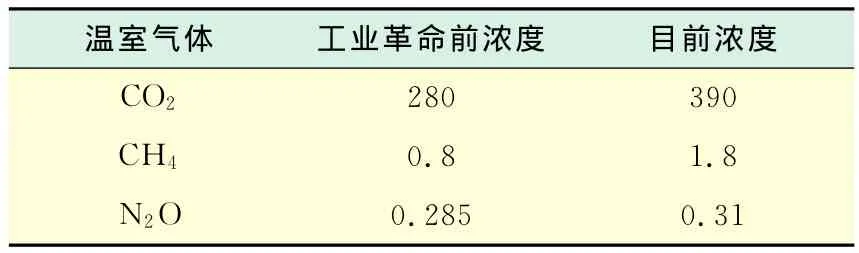
表2 工业革命前和目前大气中温室气体浓度［1］Tab.2 Greenhouse gas concentrations at present and pre－Industrial Revolution［1］mL／m3

对于某一区域，由于时间变化所引起的地表温度差异对辐射强迫影响的计算式为

式中，ΔFt为总时间t下辐射强迫的年均值；ΔF （t′）为计算区域在各不同时间段t′下的辐射强迫.而就全球而言，温室气体的辐射强迫还应考虑到不同地域之间表面温度的差异，即应将各地域的ΔFt再对其相应的地表面积A′进行积分晴天无云情况下进行，忽略散射的影响.

d.辐射方案采用美国大气与环境研究中心（AER）的RRTM－LW长波辐射传输模型，该模型以大气分子光谱资料HITRAN2004为基础，通过相关k分布模式，将计算波长区间划分为16个连续的谱带，每个谱带的k分布由逐线模型直接获得［7－8］.

3 地表温度时空差异对辐射强迫影响的分析与预测

式中，ΔFs为考虑了地表温度的时空差异后，温室气体的平均辐射强迫；A为地球的总表面积.根据式（2）～（3）进行计算时，地球的区域与时间划分如表1所示，计算中所用到的其它初始条件与假设为：

a.将地表温度作时空积分处理时，不同时间与地域下的大气温度及压力廓线均取自如表1所示的相应的气候模式；当采用地表平均温度288.15K计算时，所用到的气候模式为代表全球平均状况的美国标准大气［6］.

b.对流层顶选在大气温度随高度增加由降低转为不变的第一次转折点处，将地球假设为相应区域温度下的黑体.

c.计算波长区间为3～1 000μm，所有计算均在

表3将利用时空积分与均一处理方法各自得到的CO2，CH4和N2O的辐射强迫ΔFs和ΔFa进行了比较.考虑到气候带划分的对称性，表3中仅计算了北半球的数据.从表3可以看出，温室效应的强弱与地表温度存在着正相关的特性，即随着地表温度逐渐增加，各温室气体的年均辐射强迫ΔFt也呈上升趋势，热带地区达到最大，温室效应最为严重.但相对于CH4与N2O，由于CO2自身较大的浓度基数，使得不同地域的ΔFt，CO2对时间的积分表现出了较大差异，热带和寒带地区相差达1.02W／m2.因此经过空间积分后，ΔFs，CO2和ΔFa，CO2的差别达到了0.12W／m2，相当于6%的偏差.而CH4与N2O在大气中属于微量气体，其相对较小的辐射强迫受时间、地域差别的影响也较小，经时空积分与均一化处理不同方法所得到的辐射强迫则表现出了较好的吻合性，两者差别均只有0.01W／m2，偏差小于2%.

表3 温室气体辐射强迫Tab.3 Radiative forcing of greenhouse gases W／m2

由于CH4是大气浓度仅次于CO2的首要微量温室气体，图1与表4利用上述两种方法将这两种气体在未来100年内的辐射强迫进行了预测.CO2自工业革命以来，大气浓度呈持续增长趋势，根据美国海洋与大气管理局地球系统研究实验室所公布的数据，其2000～2010年间的平均年增长率约为每年2.1mL／m3；而CH4在1998～2006年间，增长出现停滞，浓度基本维持在1 745μL／m3的水平上，直到2007年才又开始以约每年10μL／m3的速度出现显著增长［9］.因此图1及表4中，CO2的年增长率取为实际值每年2.1 mL／m3，CH4分别取了每年1，5，10和15μL／m3的4种不同的年增长率，两种气体的初始浓度均取当前值（见表2）.

从图1及表4可以看出，随着CO2与CH4大气浓度的逐渐增加，将地表温度进行时空积分后所得到的辐射强迫均大于均一化处理方案，但CO2辐射强迫受计算方法的影响更大.如表4所示，到了2112年，CO2两种计算方法下所得到的ΔFs，CO2和ΔFa，CO2分别为4.15，3.86 W／m2，两者的绝对差值达到了0.29 W／m2，比当前差值0.12 W／m2的2倍还多，相对差别则增长到7%，与当前偏差相比增长了1个百分点.而CH4即使按照表4中最大的年增长率15μL／m3，100年后，其ΔFs，CH4也仅比ΔFa，CH4大0.03 W／m2，偏差只有3%.在地球能量平衡中，凡可能引起能量流变化0.1 W／m2的情况，都必须给予认真考虑［3，10］.因此，对于大气中含量最大的温室气体CO2，地表温度均一化的处理方案将会造成辐射强迫的计算值偏低，并且随着其大气浓度的不断加大，偏差还将明显增加；但是对于以CH4为首的其余微量温室气体，即使浓度出现大幅增加，地表温度的时空差异对其辐射强迫也不会产生显著影响，在温室效应的分析计算中采用地表平均温度不会影响到计算结果的准确性.

图1 辐射强迫随时间变化关系Fig.1 Radiative forcing variations with time

表4 2112年CO2与CH4辐射强迫预测值Tab.4 Predictiver adiative forcings of CO2and CH4in 2112

此外，图1说明，CH4作为大气中的首要微量温室气体，目前，其所产生的辐射强迫大约已经占到了CO2的25%.但是，CH4辐射强迫的增长速率明显小于CO2，而且它在大气中会与OH－自由基发生化学反应，具有较短的大气寿命，大约为9～15年［11］.如果能够维持其产生与消除的近似平衡，就有可能使其浓度像在1998～2006年间那样保持基本稳定，从而显著缓解由于CO2浓度持续上升对全球变暖所施加的巨大压力.如表4所示，如果依照CH4现在10μL／m3的年增长率，到了2112年，除去CO2所引起的温室效应，CH4会额外再贡献相当于CO2温室效应19%的辐射强迫；但是如果将浓度增长控制在每年1μL／m3，CH4的辐射强迫随时间推移则几乎没有增加，100年后其值也仅为CO2的11%.反之，如果CH4浓度在现有基础上继续增加，达到每年15μL／m3的增长率，100年后的辐射强迫将达到0.96 W／m2，是目前浓度增长情况下的预测值0.80 W／m2的1.2倍.所以如果能够减少CH4排放量，实现其浓度的缓慢增长，有可能是一个在相对短的时间内减缓温室效应的有效并可行的手段.

4 结 论

分析了全球地表温度的空间和时间分布特点，分别采用将地表温度作均一化处理以及时空积分两种不同的方法，对CO2，CH4，N2O等温室气体的辐射强迫进行了计算与预测，结果表明：

a.在CO2辐射强迫的计算中，如果采用地表平均温度将会使计算值偏低，与将地表温度作积分处理后的结果相比，两者的绝对差值达到了0.12W／m2，相当于6%的偏差，而且随着CO2大气浓度的不断加大，偏差还会明显增加；但是对于以CH4为首的微量温室气体，其辐射强迫受时空影响很小，两种计算方法下的相对偏差小于2%.

b.目前，CH4所产生的辐射强迫大约已经占到CO2的25%.但是，CH4辐射强迫的年增加率明显低于CO2，如果能够将CH4浓度增长控制在较低水平上，其辐射强迫则随时间推移几乎不发生变化，从而显著缓解由于CO2浓度持续上升对全球变暖所施加的巨大压力.

［1］ Solomon S，Qin D，Manning M，et al.Intergovernmental panel on climate change，climate change 2007：the physical science basis［M］.New York：Cambridge University Press，2007.

［2］ 丁仲礼，段晓男，葛全胜，等.国际温室气体减排方案评估及中国长期排放权讨论［J］.中国科学，D辑：地球科学，2009，39（12）：1659－1671.

［3］ Hansen J，Sato M，Kharecha P，et al.Earth’s energy imbalance and implications［J］.Atmospheric Chemistry and Physics，2011，11（24）：13421－13449.

［4］ 石广玉.大气辐射学［M］.北京：科学出版社，2007.

［5］ 盛裴轩，毛节泰，李建国，等.大气物理学［M］.北京：北京大学出版社，2003.

［6］ McClatchey R A，Fenn R W，Selby J E A，et al.Optical properties of atmosphere［M］.3rd.Cambridge：Air Forca Systems Command，United States Air Force，1973.

［7］ Mlawer E J，Taubman S J，Brown P D，et al.RRTM，a validated correlated－k model for the longwave［J］.Journal of Geophysical Research，1997，102：16663－16682.

［8］ Iacono M J，Mlawer E J，Clough S A，et al.Impact of an improved longwave radiation model，RRTM.on the energy budget and thermodynamic properties of the NCAR community climate mode，CCM3［J］.Journal of Geophysical Research，2000，105：14873－14890.

［9］ Kai F M，Tyler S C，Randerson J T，et al.Reduced methane growth rate explained by decreased Northern Hemisphere microbial sources［J］.Nature，2011，476（7359）：194－197.

［10］ Trenberth K E，Fasullo J T，Kiehl J.Earth’s global energy budget［J］.Bulletin of the American Meteorological Society，2009，90（3）：311－323.

［11］ 王建兵.环境工程与科学导论［M］.3版.北京：高等教育出版社，2009.