求解二次分配问题的预处理快速蚂蚁系统

吴果林， 李学迁

（1.桂林航天工业学院理学部，桂林 541004；2.上海理工大学管理学院，上海 200093）

二次分配问题（quadratic assignment problem，QAP）是由Koopmans等［1］在1957年提出的组合优化问题.该问题可描述为给定n个设施和n个节点，两个n×n的矩阵D＝（drs）和F＝（fij）.其中drs是节点r和s之间的距离，而fij是设施i和j之间的流量.QAP是寻找一个分配方案，使得每一个设施分配一个节点.由于设施的数量等于节点的数量，故每一个分配方案相当于整数集｛1，2，…，n｝中的一个排列.QAP的目标是寻找整数集｛1，2，…，n｝中的一个排列，最小化目标函数

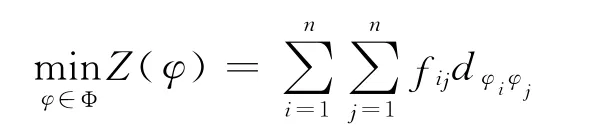
其中，Φ为整数集｛1，2，…，n｝所有排列的集合，φ为Φ中的一个排列（或问题的一个解），φi给出了设施i在当前解φ上的节点.

Sahni等［2］于1976年证明QAP是一个NP－难的优化问题，因此当问题的规模超过30时，寻找问题的最优解就变得不切实际，一个切实可行的办法是使用元启发式算法以便在合理的时间内找到高质量的解.当前用于求解QAP的元启发式算法有遗传算法［3］、模拟退火算法［4］、禁忌搜索算法［5－6］、蚁群优化算法［7－13］和迭代局部搜索算法［14－15］等.

在过去的近20年里，蚁群优化算法被用于求解许多组合优化问题［16］.事实上，对于二次分配问题中结构化的、现实生活例子，蚁群优化算法是已知的求解QAP的最好算法之一.本文调查分析了快速蚂蚁系统（fast ant system，FANT）［10－11］，给出了预处理快速蚂蚁系统（preprocessing fast ant system，PFANT）.该算法在构建问题的解时预先进行了搜索，挑选那些质量较优的解参与局部搜索，并设置动态的算法参数，防止算法陷入局部最优解，出现停滞.这种对FANT算法的改进既保持了其运行前期收敛速度快的优点［11］，拓宽了算法的搜索范围，又改进了解的质量.数值实验进一步表明，预处理快速蚂蚁系统在求解结构化的、现实生活的例子保持蚁群优化算法的优越性；在求解随机产生无结构、网格距离例子时，其性能与求解这两类例子的最好算法——禁忌搜索算法（robust taboo search，RTS）［6］不相上下.

1 快速蚂蚁系统

受蚂蚁系统算法的启发，Taillard开发了求解QAP的蚁群优化算法，称为快速蚂蚁系统［10－11］.在FANT算法中，解的构建是由人工蚂蚁通过随机地选择还没有分配的设施i，利用概率选择规则将其分配到空闲的节点j上，即

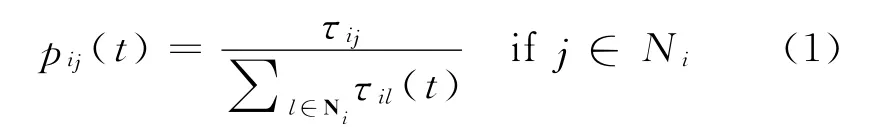
式中，τij为分配设施i到节点j上的权重；Ni为设施i可分配的节点.

FANT算法不同于其它蚁群优化算法的地方主要是人工蚂蚁的数量和信息素更新管理.FANT算法仅使用一个人工蚂蚁，单个人工蚂蚁导致该算法快速寻找到一个质量较好的解归咎于局部搜索算法的引入和相当特殊的参数设置.另一个不同于其它蚁群优化算法，是信息素更新管理，FANT算法不使用信息素蒸发.初始所有的信息素都设置为1，每一次迭代后信息素更新方式为

式中，Jφ为当前解φ的目标函数值；Jφib为迭代最优解φib的目标函数值；r和R为两个参数.r的值在算法运行过程中可以发生改变，初始值设为1，而R为固定常数.除按式（2）的更新规则更新信息素之外，信息素与参数r还将在两种情况下发生改变：a.如果迭代最优解φib发生改变，则参数与所有的信息素全都重新设置为1；b.当人工蚂蚁构建的解与迭代最优解φib相同时，参数将增加1个单位且所有的信息素设为r.

设信息素矩阵为Γ＝（τij）n×n，初始，令r＝1，τij＝r（i，j＝1，2，…，n），迭代最优解为φib，则FANT重复执行如下步骤（算法1）：

步骤1 利用式（1）构建问题的当前解φ；

步骤2 利用局部搜索技术改进当前解φ，为方便计仍记为φ；

步骤3 如果Z（φ）＜Z（φib），则φib＝φ，并设r＝1，τij＝r（i，j＝1，2，…，n）；

步骤4 按式（2）的更新方式更新信息素矩阵Γ.

2 预处理快速蚂蚁系统

从前面的叙述可以看出，FANT试图设计一种能够整合重点搜索迭代最优解和解构建时探索性的算法.也就是说，一方面通过信息素更新，FANT不断地增加迭代最优解的权重，使得算法在迭代最优解邻域选择问题的解；另一方面，当算法出现停滞时（FANT以构建解等于迭代最优解作为判断标准），重新设置信息素，并令r＝r＋1，降低迭代最优解与算法构建解所对应节点信息素增加的比重，减少迭代最优解所对应节点的权重，拓宽解的搜索范围，增加算法构建解的探索性.然而，从实验的结果来看，FANT算法解的质量并没有达到预期效果，只是在算法运行的初期，FANT总体上比其它算法要好一些，在算法运行的后期，其解的质量比其它算法要劣［11］.即FANT算法初期收敛速度快，后期易出现停滞.出现这种现象，与FANT算法信息素更新策略有关.由于FANT算法在每次出现新的迭代最优解时，信息素重新设置为1，迭代最优解对应的节点信息素设为R，算法始终在迭代最优解邻域寻找问题的解，故算法运行初期收敛速度快.易见，这样处理的结果是算法容易陷于局部最优解，产生停滞.尽管FANT算法设计了跳出局部最优解的策略（当人工蚂蚁构建的解与迭代最优解φib相同时，参数将增加1个单位且所有的信息素设为r），但这种方式所需迭代次数太多，代价太高.关于这一点，可从下面的分析看出.

设FANT在t次迭代产生的迭代最优解φib，信息素矩阵为Γ＝（τij）n×n，τij＝r且r＝1，进一步假设此解φib为局部最优解，算法出现停滞.下面计算FANT算法跳出局部最优解所需迭代的次数.由于FANT算法采用当迭代产生的解与迭代最优解φib相同时，重新设置信息素r，降低迭代最优解权重的方法，改变停滞现象.为此，先计算第一次当前解与迭代最优解φib相同（即第t＋k1次迭代产生的解等于迭代最优解φib）时，FANT算法所需迭代次数，记为k1.根据FANT算法，每次迭代时，当前解对应节点的信息素增加1；迭代最优解φib对应节点的信息素增加R.故第t＋k1次迭代时，信息素矩阵Γ每一行元素和都为n＋k1（R＋1），迭代最优解φib对应的每一个节点的信息素应小于等于k1（R＋1）＋1（此值为每次迭代时当前解等于迭代最优解时信息素的值）.设在第t＋k1次迭代时，迭代最优解作为当前解的概率P，由概率乘法公式

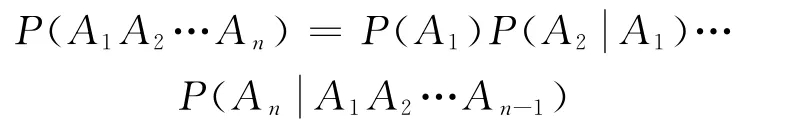
则P应满足

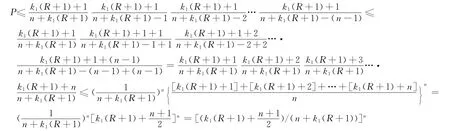
表1给出了QAP规模为25，50，100，选择概率为0.1，0.5，0.9，重新设置信息素为1，2，…，6时，FANT算法所需迭代的次数，R的取值均为6.

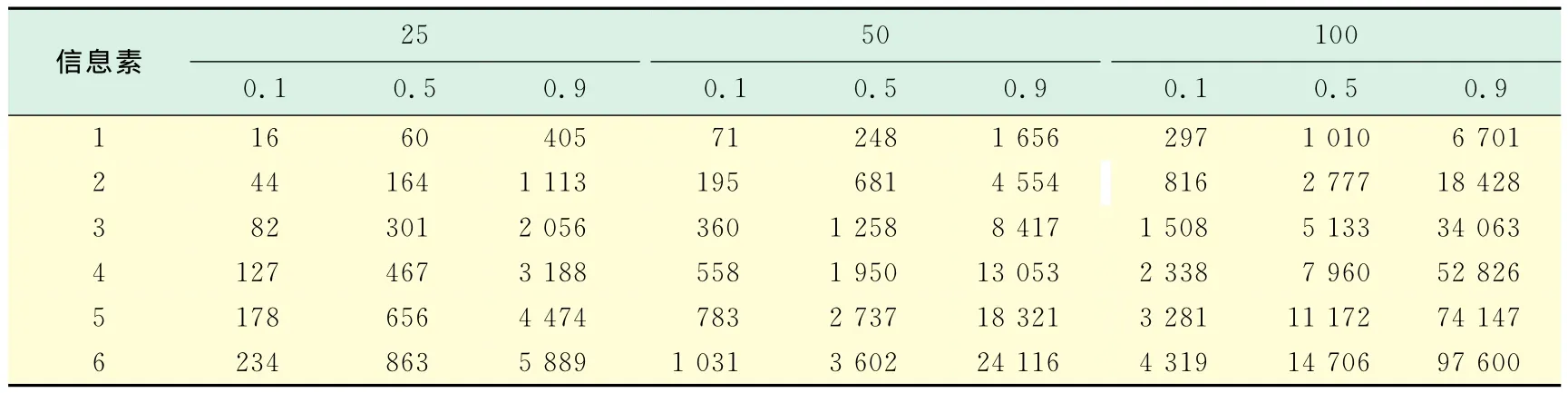
表1 跳出局部最优解的迭代次数Tab.1 Iterations times of jumping out of local optimal solution

从表1可以看出，要以较高的概率跳出局部最优解，算法所需的迭代次数非常多.以QAP规模50为例，若以0.9的概率取得局部最优解，算法至少需要迭代1 656次.由于算法每次迭代所需的时间为O（503），故算法跳出局部最优解的时间花费至少为1 656×O（503），这个数值已经超过RTS［6］算法求解QAP规模为50的迭代1 000×50次所需的时间（RTS每次迭代所需的时间为O（502）），而RTS算法迭代1 000×50次得到问题的解常常作为其它算法求QAP时比较的参照文献［8，14－15］.也就是说，对于规模为50的QAP实例而言，FANT算法以0.9的概率跳出局部最优解的时间大于RTS算法1 000×50次迭代的时间.由表1不难得出，QAP其它规模的例子同样也有类似的结果.综上所述，FANT算法设计跳出局部最优解的策略所需迭代次数太多，算法后期很少改进算法解的质量.

尽管有上述不足，但FANT算法仍然是求解QAP的非常有竞争力的算法，文献［12－13］给出了两种改进的FANT算法.事实上，仔细分析算法1的流程不难发现，步骤2是对步骤1产生的解利用局部搜索进行改进，而改进后解质量的好坏很大程度取决于步骤1产生解的质量.因此，可以对步骤1进行改进，如对步骤1产生的解进行预处理，以便较高质量的解参与步骤2的搜索改进.由于步骤1构建解是不断通过随机选择一个设施由概率选择式（1）分配一个节点得到，故对于每一个设施i分配的节点φi，可以比较与前次迭代产生的解所对应的设施i的节点φ′i是否相同.若φi≠φ′i，将前次迭代解对应的两个节点φi，φ′i的位置进行交换，再比较交换后解的质量；若质量优于交换前的，则设施i分配节点φi，否则设施i还是分配原来的节点φ′i.上述方法通过不断地重复，最终得到改进的迭代解.易见，改进后的迭代解剔除了那些迭代过程中产生的质量较劣的解，使得每次迭代产生的解始终以较好的解参与步骤2的局部搜索，减少一些无为的迭代与局部搜索，保证更好质量的解产生.当然，上述改进也易使算法快速陷入局部最优解，产生停滞.为防止或减少该现象的发生，在算法每次得到一个新的迭代最优解时重新设置一个新的r值，记为r（t），区别于原算法每次重新设置r都等于1.

另一方面，由算法1可知，FANT算法采用固定参数R的策略，这种固定参数的策略对于规模较小的QAP例子容易过早陷入局部最优解.而对于规模较大的QAP例子由于迭代最优解的权重较轻，算法收敛速度较慢.为此，文献［13］给出了一种变参数的FANT算法，实验证明，改进了的算法求解QAP的质量有较大的提高.借鉴文献［13］的思想，为进一步简化运算，针对不同规模QAP采用不同的参数R的策略，记为R（n）.因此，改进后的算法信息素更新方式为

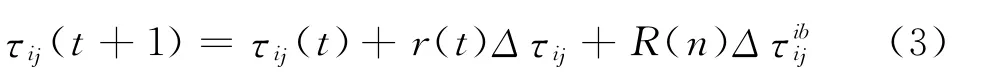
综上所述，可以对FANT算法作如下两点改进：其一，在FANT算法解的构建步，对每一个设施分配的节点进行预处理，判断该分配是否改进上一次迭代解的质量，若改善，则分配该节点，否则，保留原迭代解分配的节点；其二，在FANT算法信息素更新步，由式（3）取代式（2）作为算法的信息素更新策略.改进后的FANT算法称为预处理快速蚂蚁系统（PFANT），其算法流程为：

设信息素矩阵为Γ＝（τij）n×n，初始令r（0）＝1，τij＝r（0）（i，j＝1，2，…，n），初始解为φ，迭代最优解为φib，则PFANT重复执行步骤（算法2）为：

步骤1 考查由式（1）分配的每一个节点的能否改进上一次迭代解φ的质量.若改善，则分配该节点；否则，保留原迭代解分配的节点.为方便计构建后的解记为φ；

步骤2 利用局部搜索技术改进当前解φ，仍记为φ；

步骤3 如果Z（φ）＜Z（φib），则φib＝φ，重新设置信息素τij＝r（t）（i，j＝1，2，…，n，t＝1，2，…）；

步骤4 按式（3）的更新方式更新信息素矩阵Γ.

3 数值实验

这一部分选择QAPLIB中的例子运行PFANT和FANT算法.实验的硬件环境为Pentium（R）4 2.5GHz处理器，80GB硬盘，256MB内存，Microsoft Windows SP3操作系统，开发工具为VC＋＋6.0.对于FANT算法，参数R＝6；PFANT算法参数R＝［2n］，其中［］为取整运算，参数r随着迭代最优解φib的改变在1与2之间不断地取值.实验以RTS算法迭代1 000n次所需的时间作为迭代终止条件.实验采用QAPLIB中的例子按文献［17］分为4类.第一类，随机产生无结构问题，这类问题是根据均匀分布随机产生距离流量矩阵的问题.第二类，随机产生网格距离问题，这类问题的距离来源于一个网格，节点与节点的距离定义为网格上节点之间的曼哈顿距离.第三类，现实问题，这类问题是从实际问题抽象出来的.第四类，模拟现实问题，因为第三类现实问题规模较小，所以这类问题是根据现实问题的特点随机产生的较大规模的问题.另外，考虑到规模小于20的问题容易求解，这里只测试规模大于等于20的问题，数值实验结果见表2.表中给出的结果是超出已知最优解的百分比，最好的结果用斜粗体表示.

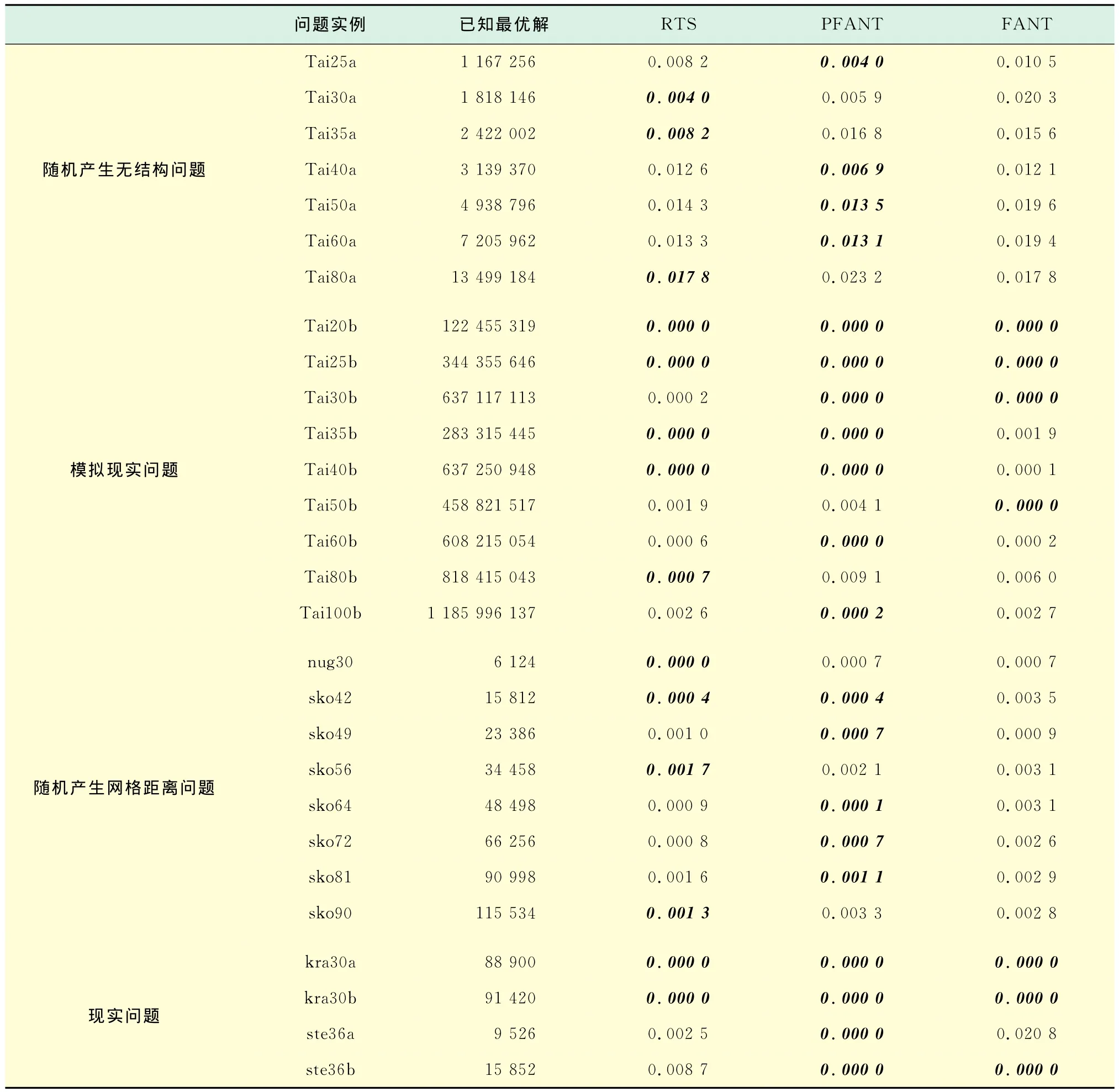
表2 PFANT算法的测试结果Tab.2 Testing result of the PFANT algorithm

尽管算法解的质量很大程度依赖所求例子［17］，但从表2仍然不难发现，PFANT算法解的质量较FANT算法有较大幅度的提升，总体上要优于FANT算法，例外的只有Tai 35a，Tai 80a，Tai 50b，Tai 80b.对比RTS算法，在RTS算法求解有较大优势的随机产生无结构与网格距离例子中，PFANT算法总体上质量也稍优于RTS算法；至于现实问题及模拟现实问题，PFANT算法全面优于RTS算法，例外的只有Tai 50b，Tai 80b.相对MMAS［8］，ILS［14］，HILS［15］算法在现实问题及模拟现实问题优于RTS算法，在随机产生无结构及网格距离问题逊于RTS算法而言，PFANT算法求解QAP上有较大提高.

其次，考察FANT与PFANT算法跳出局部最优解时重新设置信息素的次数，表3（见下页）给出了两算法求解上述4类问题的结果.从表3明显可以看出，上述4类问题的每一个例子，PFANT算法重新设置的次数都小于或等于FANT算法.出现这种情况的原因是由于PFANT算法在每次迭代构建问题的解时都预先进行了搜索，剔除了那些质量较劣的解参与局部搜索.在相同的迭代时间内，算法能在局部最优解更广的邻域内搜索，增加发现更优的局部最优解的机会，减少了重新设置信息素的次数.

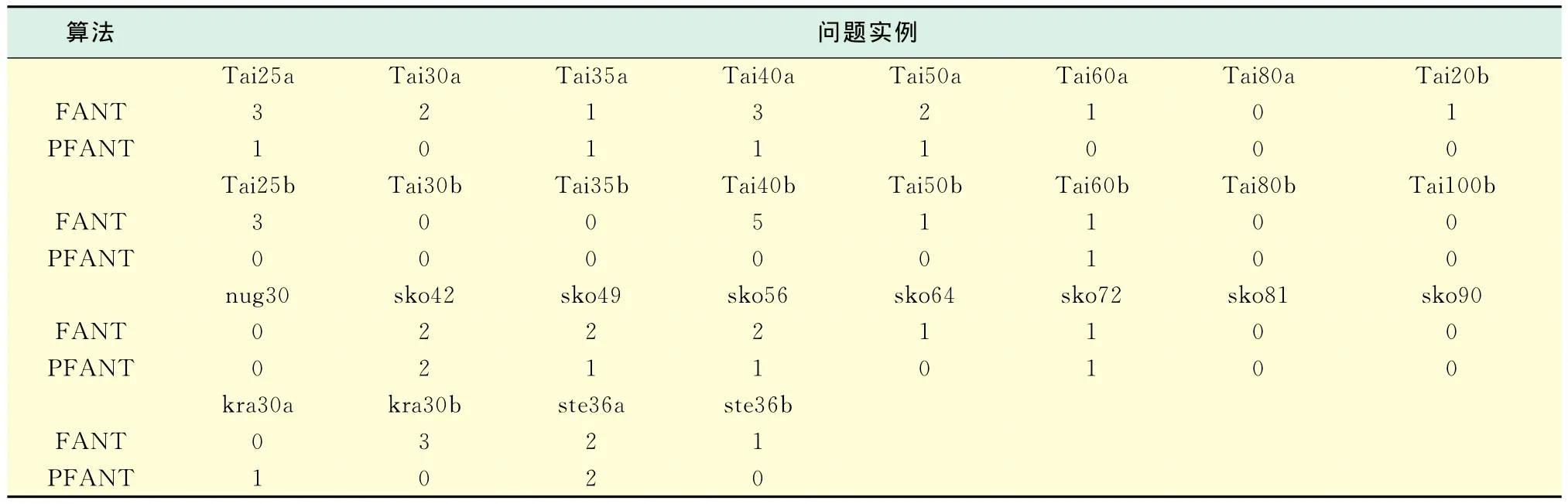
表3 FANT与PFANT算法重新设置信息素的次数Tab.3 The times of resetting pheromone in the FANT and PFANT algorithm

4 结 论

尽管FANT算法在信息素更新管理与解的构建方面较其它蚁群优化算法作了较大的改进，为求解不规则QAP例子最有竞争性的算法之一［9］，但也有明显的缺点（如算法前期收敛速度较快，后期速度较慢，易发生停滞现象等）.通过分析FANT算法跳出迭代最优解的策略，指出算法易发生停滞现象的原因，并提出了改进的方法，得到一种求解QAP的新算法——预处理快速蚂蚁系统（PFANT）.理论与实验分析表明，PFANT算法较大程度地改进FANT算法的缺点，拓宽了算法迭代最优解邻域的搜索范围，减少了重新设置信息素的次数，改善了QAP解的质量.

［1］ Koopmans T C，Berkmann M J.Assignment problems and the location of economic activities［J］.Econometrica，1957，25（1）：53－76.

［2］ Sahni S，Gonzalez T.P－Complete approximation problems［J］.Journal of the Association of Computing Machinery，1976，23（3）：555－565.

［3］ Ahuja R K，Orlin J B，Tiwari A.A greedy genetic algorithm for the quadratic assignment problem［J］.Computers and Operations Research，2000，27（10）：917－934.

［4］ Connolly D T.An improved annealing scheme for the QAP［J］.European Journal of Operational Research，1990，46（1）：93－100.

［5］ Skorin－Kapov J.Tabu search applied to the quadratic assignment problem［J］.ORSA Journal on Computing，1990，2（1）：33－45.

［6］ Taillard E D.Robust taboo search for the quadratic assignment problem［J］.Parallel Computing，1991，17（4／5）：443－455.

［7］ Maniezzo V，Colorni A.The ant system applied to the quadratic assignment problem［J］.IEEE Transactions on Knowledge and Data Engineering，1999，11（5）：769－778.

［8］ Stützle T，Hoos H H.MAX－MIN ant system［J］.Future Generation Computer Systems，2000，16（8）：889－914.

［9］ Gambardella L M，Taillard E D，Dorigo M.Ant colonies for the quadratic assignment problem［J］.Journal of the Operational Research Society，1999，50（2）：167－176.

［10］ Taillard E D.FANT：fast ant system.Technical report IDSIA－46－98［R］.Lugano：IDSIA，1998.

［11］ Taillard E D，Gambardella L M.Adaptive memories for the quadratic assignment problems.Technical ReportIDSIA－87－97［R］.Lugano：IDSIA，1997.

［12］ 吴果林，刘登峰.改进的快速蚁群系统求解二次分配问题［J］.桂林航天工业学院学报，2012，17（4）：424－427.

［13］ 吴果林.变参数的快速蚂蚁系统求解二次分配问题［J］.科学技术与工程，2013，13（7）：324－328.

［14］ Stützle T.Iterated local search for the quadratic assignment problem［J］.European Journal of Operational Research，2006，174（3）：1519－1539.

［15］ Hussin M S，Stützle T.Hierarchical iterated local search for the quadratic assignment problem［J］.Lecture Notes in Computer Science，2009，5818：115－129.

［16］ 马良，项培军.蚂蚁算法在组合优化中的应用［J］.管理科学学报，2004，4（2）：32－37.

［17］ Taillard E D.Comparison of iterative searches for the quadratic assignment problem［J］.Location Science，1995，3（2）：87－105.