分类监督半定嵌入算法

董文明， 孔德庸

（1.新疆农业大学水利与土木工程学院，新疆乌鲁木齐 830052；2.乌鲁木齐新数元测绘有限公司遥感室，新疆乌鲁木齐 830052）

0 引 言

维数约简方法一直都是模式识别、机器学习、多元统计分析等领域的重要研究课题之一，而传统的维数约简方法如：主成分分析（PCA）［1］、多维尺度变换（MDS）［2］及判别分析（MDA）［3］等大多都是线性降维方法，即假设所研究的数据集在统计意义下具有全局线性结构，并且构成数据集的各变量之间是独立无关的。因此，可以用欧氏空间这种全局线性空间来作为数据集存在的几何空间，在这样的空间中欧氏距离可以被用于数据分析，从而使得线性降维方法在欧氏空间中是有效的。但在许多实际问题中所要研究的数据集往往呈现出高度的非线性，这时再采用常规的线性维数约简方法就不能很好地描述数据的内在结构。目前已涌现出了许多优异的流形学习研究算法，如核主成分分析（kernel PCA）［4－5］、局部线性嵌入算法（Locally Linear Embedding，LLE）［6］、等度规特征映射算法（ISOMAP）［7］、拉普拉斯特征映射（Laplacian Embedding）［8］等；这些算法已经在数据的可视化与可听化、人脸识别、文本分类以及图像处理等方面得到了较好的效果。

文中将对2004年Weinberger［9］提出的一种新的流形学习算法——半定嵌入算法进行研究，从新的角度去研究SDE算法的监督形式，给出两种新的监督型SDE算法。

1 半定嵌入算法（SDE）简介

SDE算法在本质上是对核主成分分析算法的改进，它与核主成分分析算法的不同点在于：前者通过一个非线性映射φ将原空间中的数据点映射到高维特征空间，然后在特征空间中应用PCA方法，从而达到维数降低的目的；然而非线性映射φ通常是通过定义适当的内积核函数来实现的，所以根据所选择的核函数不同，降维的结果也会大不相同；SDE算法则是通过考察原数据点与经过非线性映射φ变换后的特征空间中的数据点之间的关系来构造满足特定条件（保持映射前后相邻数据点之间的距离不变）的核函数，然后在特定的高维特征空间中应用PCA方法达到降维的目的。

SDE算法的具体步骤如下：

第一步：对于给定的数据集X＝｛xi，i＝1，2，…，n｝，其中xi∈Rd，n为样本点的个数，计算任意两点间的欧氏距离，根据计算出的欧氏距离，选出数据集中任意一点xi的K个邻近点，K＜＜n；然后根据所选出的邻近点构造二进制矩阵Γn×n，如果xj是xi的近邻点，则Γij＝1，否则，Γij＝0。

第二步：通过求解如下的半定规划问题，构造核矩阵K（Kij＝（φ（xi）·φ（xj））），令Gij＝（xi·xj）：

Kii＋Kjj－Kij－Kji＝Gii＋Gjj－Gij－Gji当且仅当Γij＝1。

第三步：求解特征方程Nλα＝Kα；由于求得的各个特征值都是非负的，于是样本X的第i主成分为：

从上述算法的具体步骤中可以看出，该算法的核心部分就是求解上述半定规划问题［10］，从而构造满足条件的核矩阵。下面简要地分析一下上述半定规划问题的目标函数和约束条件所对应的具体含义。

由于我们要构造的是核矩阵，所以首先要加入约束K≥0，即要使所求的核矩阵为半正定的；而上述半定规划问题的第二个约束则是要将映射后特征空间中的数据点中心化，也就是说要使：

这个式子可等价为以下等式：

最后一个约束则是反映了原数据点与经过非线性映射φ变换后的特征空间中的数据点之间的关系，即保持两邻近点之间的距离不变：

对于上述半定规划问题的目标函数，则是要在保持局部几何结构不变的前提下尽量使两点之间的距离增大，即要在满足约束的前提下使：

达到最大，由Kij和Gij的定义可将H化简如下：

上述半定规划问题可以用SeDuMi 1.0软件包进行求解，该软件包的运行环境是Matlab，具体操作可参见文献［11］。

SDE算法由于在降维过程中不考虑样本点的标签信息，从本质上讲是一种非监督的流形学习算法，所以并不适合分类问题的降维，在文献［12］中基于无监督的SDE算法提出了一种有监督的算法，称为SSDE，当该算法用于分类问题的降维时，为了提高降维后分类的正确率，使得在低维空间中，同类样本点尽可能地聚在一起。因此，在求解xi的K个最邻近点的时候，要求选出的K个最邻近点与xi具有相同的标签信息，即在选择xi的K个最邻近点的时候，是在与xi类别相同的样本点中进行选取的，这样就保证了xi与其K个最邻近点隶属于同一类别。SSDE算法的具体实现步骤如下：

第一步：给定数据集X＝｛xi∈Rd，i＝1，2，…，n｝，以及与数据集X相对应的标签信息ω＝（ω1，ω2，…，ωn），对于数据集中的任意一点xi，首先根据xi的标签信息选出与xi具有相同标签信息的样本点组成集合Δi，然后在Δi中根据欧氏距离的大小选择K个最邻近点，K＜＜n；然后根据所选出的邻近点构造二进制矩阵Γn×n，如果xj是xi的近邻点，则Γij＝1，否则，Γij＝0。

SSDE算法接下来的步骤与SDE算法的后两步相同。

从上述SSDE算法的具体实现步骤来看，该算法与原始的SDE算法唯一的不同点就在于邻近点的选择上，SSDE算法充分利用了所给样本点的标签信息，使得数据集X中的同类样本点在降维后尽可能地聚在了一起。

2 两种新的SSDE算法

2.1 基于权重的SSDE算法

由于监督型的流形学习算法目的就是要充分利用样本点的标签信息，使得降维后在低维空间中的同类样本点尽量地聚在一起，结合SDE算法本身的特性（保持样本点的局部结构不变，即保持降维前后邻近样本点之间的距离不变），只要在原空间中利用样本标签的信息，使得同类样本点之间的欧氏距离变小，不同类样本点之间的欧氏距离变大，即通过改变原空间中样本点的分布（同类点相互靠近），来达到使降维后低维空间中的同类样本点尽量聚在一起的目的。

基于上述讨论，我们对任意两点间的欧氏距离定义如下的权重：

式中：Mij——数据集中任意两点xi与xj之间的欧氏距离；

ωi，ωj——分别代表了点xi与xj的标签信息；

下面给出基于权重的SSDE算法的具体步骤：

第一步：给定数据集X＝｛xi∈Rd，i＝1，2，…，n｝，以及与数据集X相对应的标签信息ω＝（ω1，ω2，…，ωn），首先计算任意两点间的欧氏距离，得到欧氏距离矩阵M，再根据样本点的标签信息对两点间的欧氏距离做如下的改进：

并且用改变后的距离M′ij来代替原来两点间的欧氏距离，根据改变后任意两点间距离的大小，选出数据集中任意一点xi的K个邻近点，K＜＜n；然后根据所选出的邻近点构造二进制矩阵Γn×n，如果xj是xi的近邻点，则Γij＝1，否则，Γij＝0。

基于权重的SSDE算法接下来的步骤与SDE算法的后两步相同。

2.2 基于最佳距离度量的SSDE算法

上述基于权重的SSDE算法虽然可以达到使降维后低维空间中的同类样本点尽量聚在一起的目的，但是这种算法仅仅是利用已知样本点的标签信息机械地增大或缩小两样本点之间的欧氏距离。下面引入一种基于另一种距离度量方式的SSDE算法，即基于最佳距离度量的SSDE算法；首先，简单地介绍一下什么是最佳距离度量［13］。

最佳距离度量是模式识别中最佳距离度量近邻法所采用的一种距离度量形式，采用这种距离度量可使得用最近邻法分类时具有较小的错误率（相对于其它的距离度量形式而言）。基于这一特点，可以直观地认为在这样的距离度量下，同一类别的样本点能在一定程度上相互靠近；接下来我们将给出最佳距离度量的具体数学表达式。

设数据集X＝｛xi∈Rd，i＝1，2，…，n｝中的样本点分别属于C个不同的类别，我们把X中每一类所含有的样本点个数记为ni，i＝1，2，…，C；对于数据集X中的任意一点x，先根据其到其它各点欧氏距离的大小找出与x距离最近的k个邻近点xl，l＝l1，l2，…，lk；在选出的k个邻近点中，每一类所包含的样本点个数记为Wi，i＝1，2，…，C，然后根据以下表达式：

求得点x到其k个邻近点xl的最佳距离，其中：

基于最佳距离度量的SSDE算法与SSDE算法的不同点在于，选择近邻点时所用的距离度量形式不再是传统的欧氏距离，而是上述定义的最佳距离度量，下面总结一下这一算法的具体步骤：

第一步：给定数据集X＝｛xi∈Rd，i＝1，2，…，n｝，以及与数据集X相对应的标签信息ω＝（ω1，ω2，…，ωn），首先计算任意两点间的欧氏距离，然后根据欧氏距离的大小确定数据集中任意一点x的邻近区域，在邻近区域范围内根据上面定义的最佳距离度量计算点x到区域内任意一点的最佳距离，再根据所算出的最佳距离的大小选择点x的k个近邻点，然后根据所选出的邻近点构造二进制矩阵Γn×n，如果xj是xi的近邻点，则Γij＝1；否则，Γij＝0。

基于最佳距离度量的SDE算法接下来的步骤与SDE算法的后两步相同。

3 数值实验

上面提出了两种监督型的SDE算法，由于这些算法主要是在分类问题的数据降维阶段进行应用，所以接下来将会把这些算法应用到不同的数据集中，并与其它的监督或非监督流形学习算法进行比较，来说明它们在分类问题降维阶段的有效性。

在下面的数值实验中所用到的数据集主要来源于UCI和USPS数据库，详细的数据属性见表1。

表1 数据属性

数值实验的具体步骤如下：

1）将原始数据的80%作为训练集，20%作为测试集，然后用PCA，SDE，MDS，SSDE，基于权重的SSDE及基于最佳距离度量的SSDE对训练集进行降维处理，所要降到的低维空间维数d用特征值分析法确定。

2）基于训练集和降维后的低维数据训练RBF神经网络，然后用训练出的神经网络模型对测试集进行处理，得到与测试集相对应的低维数据。

3）用最近邻分类方法对降维后的与测试集相对应的低维数据进行分类，统计分类的错误率。

以上实验对每个数据集都做了10次，实验结果取10次的平均值。实验结果见表2。

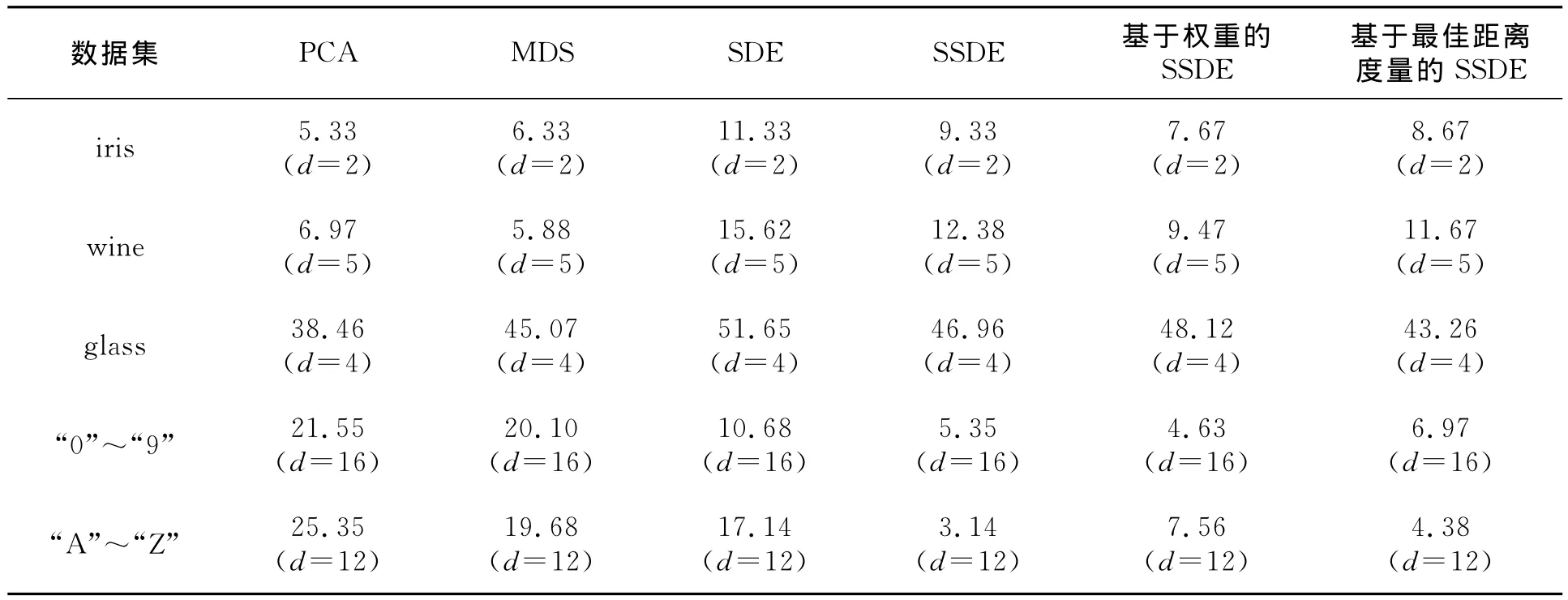
表2 平均分类错误率 %

从上述实验结果可以看出，监督型的SSDE算法对于高维数据集降维效果均要好于线性降维算法（PCA，MDS）以及无监督的SDE算法；但是对于维数较低的数据集来说，监督型的SSDE算法的降维效果就不是很好。

4 结 语

对SDE算法的监督型算法进行了研究，提出了两种新的监督型SSDE算法：基于权重的SSDE算法和基于最佳距离度量的SSDE算法，这两种算法都是在SDE算法的基础上根据样本点的标签信息修改距离的度量方式来实现无监督SDE算法到监督型SSDE算法的转变。

总体来说，监督型的SSDE算法主要是在分类问题的降维阶段进行应用，并且在高维数据的分类问题中取得了较好的效果；但是目前，关于监督型的SSDE算法在其它方面的应用研究还比较少，这将成为今后研究的一个主要方向。

［1］ I T Jollie.Principal component analysis［M］.New York：Springer-Verlag，1986.

［2］ T F Cox，M A Cox.Multidimensional scaling［M］. 2nd edition.［S.l.］：Chapman Hill，2001.

［3］ R O Duda，P E Hart，D Stork.Pattern classification［M］.2nd edition.［S.l.］：John Wiley ＆Sons，2001.

［4］ J Ham，D D Lee，D Mika，et al.A kernel view of the dimensionality reduction of manifolds［C］／／Proceedings of the Twenty First International Conference on Machine Learning（ICML-04）.Banff，Canada.2004.

［5］ C K I Williams.On a connection between kernel PCA and metric multidimensional scaling［J］.Machine Learning，2002，46：11-19.

［6］ S T Roweis，L K Saul.Nonliear dimensionality re-duction by locally linear embedding［J］.Science，2000，290：2323-2326.

［7］ J B Tenenbaum，V de Silva，J C Langford.A global geometric framework for nonlinear dimensionality reduction［J］.Science，2000，290（5500）：2319-2323.

［8］ M Belkin，P Niyogi.Laplacian eigenmaps and spectral techniques for embedding and clustering［C］／／Advances in Neural Information Processing Systems.2002.

［9］ K Q Weinberger，F Sha，L K Saul.Learning a kernel matrix for nonlinear dimensionality reduction［C］／／Proceedings of the Twenty First International Conference on Machine Learning（ICML-04），Canada，2004：839-846.

［10］ L Vandenberghe，S P Boyd.Semidefinite programming［J］.SIAM Review，1996，38（1）：49-95.

［11］ J F Sturm.Using SeDuMi 1.02，a MATLAB toolbox for optimization over symmetric cones［C］／／Optimization Methods and Software，1999.

［12］ B Y Zhang，J Yan，N.Liu，et al.Supervised semidefinite embedding for image manifold［C］／／http：www.ieee.org／ieeexplore，2005.

［13］ 边肇祺，张学工.模式识别［M］.2版.北京：清华大学出版社，1999.