一种基于模糊性理论的最优保险决策模型
2014-03-26朱佳兵王秋庭
朱佳兵,王秋庭
(武汉科技大学理学院,湖北 武汉,430065)
模糊性是普遍存在的,而信息的模糊性对人类的选择行为具有重要影响。为了更好地对信息模糊性进行分析,基于模糊性的模型相继被提出,其中,比较著名的有Choquet期望效用模型[1]、α-极大极小期望效用模型[2]、光滑模糊厌恶模型(KMM Model)[3]等。
将信息模糊性引入保险市场研究则相对较晚,国外的研究主要集中在两个方面。第一,考查模糊性对市场和市场参与者行为的影响。例如,Hogarth等[4]通过实验观察了保险人和再保险人对模糊性的行为反应,结果表明投保人和保险人对模糊性是厌恶的,即在模糊性下,保险人向投保人收取的保费和投保人愿意支付的保费都要比 “纯风险”情形下的保费高;Kunreuther等[5]对保险人的模糊性偏好与市场失效之间的关系进行了研究;Alary等[6]研究了模糊性厌恶对市场需求的影响,认为模糊性厌恶会导致对自我保险需求的增加和自我保护需求的减少;Etner等[7]研究了模糊性厌恶对医疗保险市场的影响,发现投保人对医疗保险的需求程度与其模糊性程度正相关。第二,研究模糊性下的最优保险设计问题。例如,Gollier[8]在假定投保人为模糊厌恶的情况下,运用KMM模型得到最优保险合同与模糊性结构有关和模糊厌恶的投保人对最优保险的承保范围要比其他人低的结论;Huang等[9]研究发现,在模糊性条件下,竞争性保险均衡是逆向选择还是正向选择,取决于保险人对模糊性的厌恶程度。在我国,由于保险业起步较晚,目前的研究大部分还停留在基础层面,国内几乎没有关于模糊性下保险市场以及保险定价等问题的研究。
通过对大量文献的分析发现,对于信息模糊性下的保险市场研究,大部分局限在对模糊性存在的实验或实证研究,或者只考虑单边模糊性或单个垄断性保险人等方面,而对于双边模糊性条件下的保险市场研究相对较少。
本文将保险决策研究拓展到双边模糊性范畴,即保险人与投保人均面临一定程度的模糊性情况。在假定投保人为风险厌恶、保险人为风险中性的条件下,探讨两者面临相同的模糊性程度时的市场均衡问题,给出模糊性均衡保险市场中投保人的决策模型,通过对模型的求解,得到投保人的最优保险决策。
1 模糊性理论概述
令Ω={ω1,…,ωn}为给定的自然状态集,Σ为Ω上一代数,行为(随机变量)ξ:Ω→为Ω中每一个状态指定了一个结果,v(ω)为基本事件ω发生的概率。不存在模糊性时,就是指定给Ω的确定的先验概率,依据主观期望效用理论(SEU),可以得到决策者对于行为的偏好关系集,从而得到决策者的最优选择。然而在实际中,决策者往往得不到相关事件的准确信息,获取的信息多半具有模糊性,这样就导致了决策者的行为无法用期望效用函数来描述。为了考虑信息的模糊性,Gilboa等[10]采取了如下方法:用已经存在的不同专家意见或多个先验概率表示信息的模糊性,用一不可加概率测度表示决策者的信任函数,用Choquet积分表示其偏好。 一不可加概率测度或容量v就是一集函数v∶Σ→,满足v(∅)=0;v(Ω)=1;∀A,B∈Σ∶A⊆B,有v(A)≤v(B)。称v是凸的,如果满足v(A∪B)+v(A∩B)≥v(A)+v(B)。
给定凸的容量v,定义其核为:
Core(v)={p|①p为Ω上一测度;②∀A⊆Ω,p(A)≥v(A);③p(Ω)=v(Ω)}。
关于Core(v),Huber等[11]给出如下性质:
v=min{p|p∈Core(v)}
(1)
由上述定义和性质可知,Core(v)实际上可以看成是决策者指定给Ω的可选概率分布,或者说是决策者对未知信息(模糊性程度)的估算(测度),而v则是其核Core(v)中“最糟糕”情况下的概率分布。由此给出模糊性程度的定义。
定义1设决策者1和决策者2可选的先验概率集分别为A和B,若A⊂B,则称决策者2比决策者1面临更多的模糊性。
若A=B,即决策者1和决策者2面临相同的模糊性,由式(1)可知,他们指定在原状态空间Ω上各状态的先验概率是相等的。
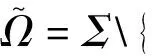
当模糊性存在时,关于决策者对行为ξ的评价U(ξ),文献[10]给出了如下定理。
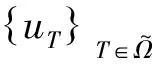
(2)
和
(3)
同时随机变量ξ对相应的不可加概率测度v的Choquet积分可以表示为:
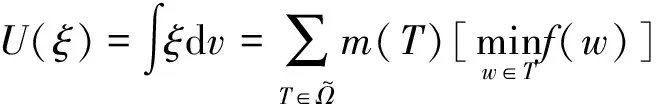
(4)
式中:Ti=T{ωi},T={ω1,…,ωn}。所有不可加概率测度组成的集合V为对自然数运算的一个线性空间。
2 模糊性下的保险市场模型
保险实际上是一种风险管理方式,而风险最终只可能有两种状态:发生或不发生,投保人根据对风险的评估来决定买何种保险。故本文对所研究的保险市场作如下假定:
(1)保险市场中有足够多的保险人和投保人,同时市场是均衡的,也就是说市场上提供了多种保险产品供投保人选择。
(2)市场只有两种可能的状态,或者说Ω={Accident, No-accident},简写为Ω={A, N}。
(3)保险人与投保人关于“风险发生几率”的信息是模糊的,即无法知道风险发生的客观概率。
对保险人来说,通过风险的汇聚,可以对同质的风险进行识别。所以,一般来说被保险人对风险的厌恶程度更强。本文假定,保险人为风险中性的,投保人为风险厌恶的。
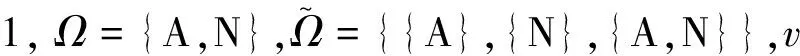
m({A})=v({A}),m({N})=v({N})
(5)
m({A,N})=v(Ω)-v({A})-v({N})=
1-v({A})-v({N})
(6)

设投保人和保险人的初始财富值分别为w0和w1,投保标的价值为d。投保人提供的保险合同为(P,I),表示保险人向投保人收取保费P,当损失d发生时,对投保人给予赔付Ι,Ι为非负数。记(ξ(A),ξ(N)) 和(ξ′(A),ξ′(N))分别为保险人和投保人在风险发生或者不发生后的财富值,u(w)为期望效用函数。购买保险(P,I)后,投保人的财富值
ξ(A)=w0-d+I-P,ξ(N)=w0-P
(7)
由式(4)知:
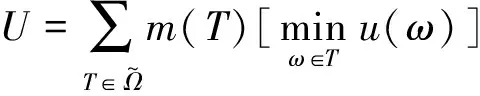
=u(ξ(A))m({A})+u(ξ(N))m({N})+
m({A,N})min[u(ξ(A)),u(ξ(N))]
(8)
对保险人来说,他希望通过出售保险来使收益最大化。出售保险(P,I)的Choquet期望效用为
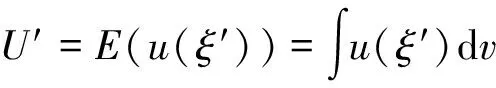
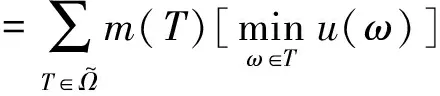
=u(ξ′(A))m({A})+u(ξ′(N))m({N})+
m({A,N})min[u(ξ′(A)),u(ξ′(N))]
(9)
式中:ξ′(A)=w1-I+P,ξ′(N)=w1+P。
由保险人为风险中性可知u(w)=w,代入式(9),化简得 :
U′=w1+P-(1-vN)I
(10)
对于均衡市场,通常是零期望赔付的,即U′-w1=0,所以有
(11)
均衡市场下,投保人选择最优保险的问题实际上就是最大化其Choquet期望效用问题,即求解如下最优化问题:
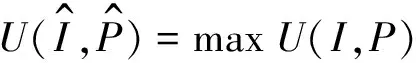
(12)
3 模型求解
因投保人为风险厌恶的,可知其效用函数的导数u″<0和u′>0,故效用函数u是单增的。
易知,当I>d时,u(ξ(A))>u(ξ(N));当I 最优化问题(12)可化为 (13) 将式(7)和式(11)代入上式,有 (14) 对P求导,有 (15) 由于模糊性的存在,故 m({A,N})=1-vA-vN>0 (16) 所以 (17) 又因为当P>(1-vN)d时, (18) (19) 随着模糊性程度的增加,即m({A,N})的增加,保险人和被保险人认为损失发生的概率m({A})和不发生的概率m({N})会相应地减少。由前面的分析知道,保险公司向投保人收取的保费P将会增加,而所支付的赔付I则会减少。尽管如此,当损失发生时,投保人依然会得到全额赔付,只不过随着投保人模糊性程度的增加,其净收益会相应地减少而已。 本文在引入模糊性的基础上讨论了一个简单均衡保险市场模型下的投保人最优决策问题。通过分析得出,在保险人与投保人面临模糊性程度相同的情况下,足额保险为投保人的最优选择,同时随着模糊性程度的增加,投保人需要缴纳的保费会相应地增加,而净收益会相应地减少。 本文考虑了保险人与投保人模糊性程度相同的情况,但并未对两者模糊性程度不同的情况进行分析,这一点还有待于拓展。再者,保险市场与再保险市场都涉及到风险管理问题,但不同于保险市场的是,再保险市场要解决的主要是对已知风险的再转移情况,能否以及怎样将模糊性理论应用到再保险市场也是值得进一步研究的。 [1] Gilboa I, Schmeidler D. Maximin expected utility with non-unique prior[J].Journal of Mathematical Economics, 1989, 18:141-153. [2] Ghirardato P, Maccheroni F, Marinacci M. Differentiating ambiguity and ambiguity attitude[J]. Journal of Economic Theory, 2004, 118:133-173. [3] Klibanoff P, Marinacci M, Mukerji S. A smooth model of decision making under ambiguity[J]. Econometrica, 2005, 73(6):1849-1892. [4] Hogarth R, Kunreuther H. Risk, ambiguity, and insurance[J]. Journal of Risk and Uncertainty, 1989, 2(1):5-35. [5] Kunreuther H, Hogarth R, Meszaros J. Insurer ambiguity and market failure[J]. Journal of Risk and Uncertainty, 1993, 7(1):71-87. [6] Alary D, Gollier C,Treich N. The effect of ambiguity aversion on insurance and self-protection[J]. The Economic Journal,2013,123:1188-1208. [7] Etner J, Spaeter S. The impact of ambiguity on health prevention and insurance[EB/OL]. (2010-04-11)[2013-08-01].http://www.beta-umr7522.fr/productions/publications/2010/2010-08.pdf. [8] Gollier C. Optimal insurance design of ambiguous risks[EB/OL].(2012-05-29)[2013-01-12].http://idei.fr/doc/by/gollier/optimalAA3.pdf. [9] Huang R J, Snow A, Tzeng L Y. Competitive insurance contracting with ambiguity and asymmetric information[EB/OL].[2014-01-15].http://www.smeal.psu.edu/rm/law-and-business-conference/competitive-insurance-contracting-with-ambiquity-and-asymmetric-information. [10]Gilboa I, Schmeidler D. Additive representations of non-additive measures and Choquet integral[J]. Annals of Operations Research, 1994, 52:43-65. [11]Huber P J, Strassen V. Minimax tests and the Neyman-Pearson Lemma for capacities[J]. The Annals of Statistics, 1973, 2:251-263.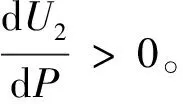
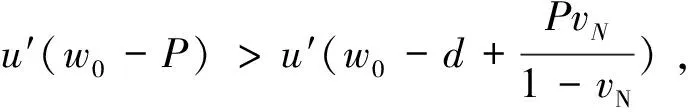

4 结语
