基于Mori-Tanaka方法的炭纤维水泥砂浆力学性能研究

周庆磊，姜翠香，曹进军

(武汉科技大学理学院，湖北 武汉，430065)

炭纤维水泥砂浆(CFRM)是由增强相炭纤维和基体水泥砂浆组成的一种具有多种功能特性的复合材料。与普通水泥砂浆相比，CFRM不仅有较强的抗拉性能和韧性，而且还有很好的耐磨性、抗干缩性、抗渗透性等，在建筑与道路工程中具有广阔的应用前景[1-4]。

在CFRM中，短切炭纤维随机分布在水泥砂浆基体内，使得从理论上研究CFRM复合材料的力学性能变得非常复杂。目前关于CFRM力学性能的研究大都建立在实验的基础上，但是实验研究成本高、过程复杂、养护期长，对测量仪器的要求也比较高，且实验方法通常也难以对材料的作用机理进行研究。

Mori和Tanaka提出平均应力概念[5]，解决了在有限体积分数条件下使用Eshelby等效夹杂原理的基本理论问题，随后，在Mori-Tanaka平均应力概念下的等效夹杂原理被广泛用于计算复合材料的力学性能。本文将Mori-Tanaka方法用于CFRM的力学性能研究，推导CFRM力学参数表达式，对炭纤维含量不同的CFRM复合材料的力学性能参数进行计算，同时通过实验获取CFRM的力学性能参数，将理论计算与实测结果进行对比分析，以期为CFRM结构性能的进一步研究提供参考。

1 实验

1.1 原材料

水泥：P·O 42.5普通硅酸盐水泥；细砂：自然河砂，重复过筛以使砂粒细小；PAN基炭纤维，其力学性能如表1所示；分散剂：选用甲基纤维素分散剂，用于对成束短切炭纤维的分散；减水剂：采用三乙醇胺减水剂。

表1 炭纤维力学性能参数Table 1 Mechanical parameters of carbon fiber

1.2 试样制备及性能测试

原料配比：水泥、砂、水、减水剂、分散剂按100∶100∶30∶0.5∶0.5(质量比)配制，PAN基炭纤维分别按0.3%、0.6%、0.9%(体积分数)掺入。

将分散剂加入水中，搅拌至完全溶解，然后加入炭纤维并搅拌使其分散，接着按比例加入水泥、砂、减水剂，滴入消泡剂，用搅拌机搅拌3 min。将制备好的炭纤维砂浆倒入模具中，振动2 min使其密实，制成40 mm×40 mm×40 mm的试块，24 h后脱模，在养护箱中养护28 d。将制备好的CFRM试样在WE-1000B液压式万能试验机上进行力学性能测试，加载速率为1 kN/s。

2 CFRM力学性能参数的理论计算

2.1 CFRM复合材料的均匀边界条件

CFRM材料结构中，炭纤维随机分布在水泥砂浆基体内，对CFRM细观结构力学问题的数学描述和定量化处理都是非常困难的。要解决这一难题，就必须对CFRM的结构进行均匀化，然后找到能够代表其力学性能的单元。

由代表单元组成的材料称为统计均匀材料，统计均匀材料受到均匀边界条件的作用，介质内的场变量就是统计均匀场。对弹性均匀场而言，有均匀应力和均匀应变两种均匀边界条件[6]。当CFRM复合材料受到均匀边界条件作用时，其统计均匀场的体积平均值可以用均匀边界值表示[7]。

2.2 CFRM中水泥砂浆基体的平均应力

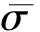
(1)

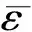
2.3 CFRM的力学性能参数

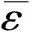
L1(ε0+εr+ε′)=L0(ε0+εr+ε′-ε*)

(2)

ε′=Sε*

(3)

式中：L1为增强相炭纤维的刚度矩阵。

由式(1)～式(3)可得：

(4)

在均匀应力边界条件下，整个复合材料的平均应变为：

(5)

由于复合材料受到均匀应力边界条件的作用(有效应力等于平均应力)，可以得出复合材料的有效刚度矩阵:

(6)

对于各向同性材料，独立的材料常数只有两个，所以其刚度矩阵可以用体积模量和剪切模量表示。四阶Eshelby张量矩阵S也可简化为一个二阶向量[9]。将两种材料的刚度矩阵和Eshelby张量矩阵S代入式(6)，得到CFRM的体积模量和剪切模量参数表达式：

(7)

(8)

式中：k0和u0分别为水泥砂浆的体积模量和剪切模量；k1和u1分别为炭纤维的体积模量和剪切模量。

2.4 应用示例

以水泥砂浆为基体材料，其中水泥、砂、水按10∶10∶3(质量比)配比，水泥砂浆基体的力学性能参数由实验获得：弹性模量为27.96 GPa，泊松比为0.27；以PAN基炭纤维为夹杂材料，炭纤维的体积分数分别为0.3%、0.6%、0.9%。，其技术参数见表1。炭纤维、水泥砂浆的体积模量和剪切模量可以通过各自的弹性模量和泊松比求出。再将以上参数代入式(7)～式(8)，求出CFRM的体积模量和剪切模量，最后计算得到CFRM的弹性模量和泊松比，计算结果如表2所示。

表2炭纤维含量不同的CFRM力学性能参数

Table2MechanicalparametersofCFRMwithdifferentcarbonfibercontents

炭纤维体积分数/%体积模量/GPa剪切模量/GPa弹性模量/GPa泊松比0.319.2311.0626.820.210.619.3211.1226.960.210.919.4011.1727.080.21

3 计算值与实测值的比较分析

炭纤维含量不同时CFRM的应力-应变计算结果与实测结果的对比如图1所示。由图1可见，计算值与实测值能较好地吻合，表明Mori-Tanaka平均应力方法适用于CFRM力学性能参数的分析计算。同时，实测值普遍略低于计算值，主要由两方面因素造成：①理论计算假设炭纤维均匀分布于砂浆基体材料中，而实际上，由于短切炭纤维是成束的，虽然分散剂在很大程度上分散了炭纤维束，但炭纤维在基体中是难以达到均匀分布的；②炭纤维的掺入会带来材料内部的气孔等缺陷。由图1还可看到，随着炭纤维体积分数的增加，计算值与实测值的误差增大，表明CFRM复合材料的力学性能并没有随着炭纤维掺量的增加而成比例地提高，这是由于随着炭纤维掺量的增加，炭纤维分布不均匀、气孔等造成的材料缺陷也会增加，使得理论假设同实际情况相差更大。 因此，Mori-Tanaka平均应力方法适用于炭纤维含量较低的CFRM复合材料力学性能参数的计算。

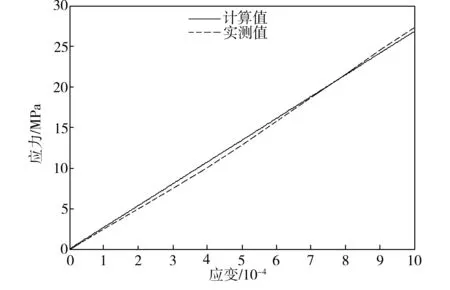
(a)c1=0.3%

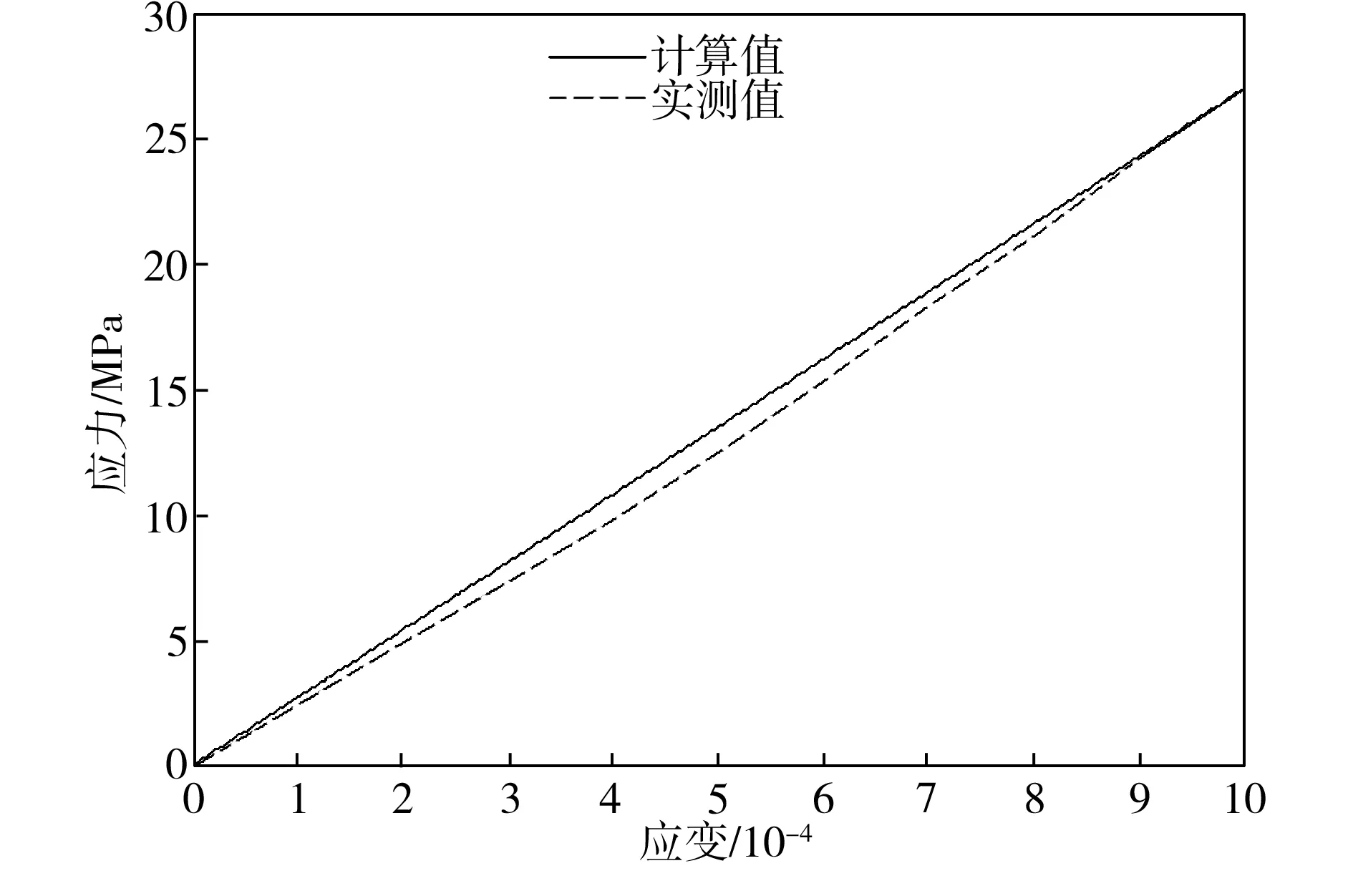
(b)c1=0.6%

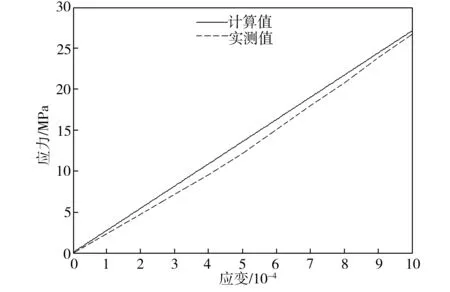
(c)c1=0.9%

图1CFRM应力-应变的计算结果与实测结果对比

Fig.1Calculatedandmeasuredresultsofstress-strainofCFRM

4 结论

(1)等效夹杂原理和Mori-Tanaka平均应力方法适用于CFRM复合材料细观结构特性的分析研究。

(2)基于Mori-Tanaka方法的CFRM力学性能参数理论计算结果普遍略高于其实测值。

(3)随着CFRM中炭纤维含量的增加，CFRM力学性能参数的理论计算值与实测值的误差有所增大。

[1] 张卫东，徐学燕.碳纤维混凝土的特性及发展前景[J].森林工程，2004,20(1):61-63.

[2] 梁福康.碳纤维混凝土[J].建筑技术,2001(1):17.

[3] Jiang Cuixiang, Li Zhuoqiu, Song Xianhui, et al. Mechanism of functional responses to loading of carbon fiber reinforced cement-based composites[J].Journal of Wuhan University of Technology:Materials Science Edition,2008,23(4):571-573.

[4] 姜翠香，钟冬望，磨季云，等.碳纤维水泥基复合材料功能响应的机理研究[J]. 混凝土,2011(5):64-66.

[5] Mori T, Tanaka K. Average stress in matrix and average energy of materials with misfitting inclusion[J].Acta Metall,1973,21: 571-576.

[6] Hashin Z. Analysis of composite materials: a survey[J]. Journal of Applied Mechanics,1983,50: 481-505.

[7] 杨庆生.复合材料细观结构力学与设计[M].北京：中国铁道出版社，2000:28-31.

[8] Eshelby J D.The determination of the elastic field of an ellipsoidal inclusion and related problems[C]//Proceedings of the Royal Society of London Series A:Mathematical and Physical Sciences,1957,241:376-396.

[9] Weng G J.Some elastic properties of reinforced solids with special reference to isotropic ones containing spherical inclusions[J]. International Journal of Engineering Sciences, 1984,22(7):846-856.