特征线坐标系下柱对称超音速流膨胀波计算方法研究

郭良斌，赵瑞兵

(武汉科技大学机械自动化学院，湖北 武汉，430081)

柱对称超音速流常见于盘状等离子体发生器[1-3]和静压圆盘止推气体轴承[4]中。气体轴承间隙内出现超音速流动时，其流动规律已不能用可压缩雷诺润滑方程来描述[5]。在圆盘止推气体轴承的超音速流中，当某一壁面有外折角时，转折尖点处会产生倾斜的膨胀波系。由于气体沿圆盘径向流动时其马赫数是变化的[4]，膨胀波上不同点处的来流马赫数并不相同，因此轴承中的膨胀波呈曲线形。

目前对轴向超音速来流的研究，多是关于其对细长旋成体的绕流的分析[6-7]。而圆盘止推轴承中，来流方向为径向来流，不同于细长体。对于圆盘止推气体轴承中柱对称超音速流膨胀波的计算方法，目前尚未见有针对性的研究成果。

左克罗等[7]给出了直角坐标系下定常二维无旋超音速流特征线法的严谨数学理论和计算方法，但其边界条件的处理也较为繁琐，缺乏物理直观性。仅讨论单壁面无膨胀波反射时，求解区域是物理平面上求解初值问题的三角形区域，按Courant 等[8]的理论，该问题属于特征线坐标系下的非特征初值问题，采用有限差分法来求解4个特征方程可以得到问题的解，但边界条件的处理较为复杂。为此，本研究借鉴Liepmann[9]引入两个黎曼不变量的方法，对特征线坐标系下的相容性方程进行积分求解，以期使边界条件的处理更加直观和简便。

1 物理模型的建立

单孔圆盘止推气体轴承的结构如图1所示。图1中，rj为节流孔半径；rs为圆盘半径；平行段半径为rO；圆盘内任意位置处半径为rx；气膜厚度为h；不平行段自O点转折，转折角为δ。

图1 单孔圆盘气体止推轴承结构示意图Fig.1 Circular gas thrust bearing with single orifice

2 数学模型的建立

给定气体轴承中二维柱对称流动气膜入口处的参数。该处环形面积是流道的最小截面，故在气体流出节流孔进入圆盘时速度满足临界条件，该处马赫数Ma1=1，平行盘内任意点处半径rx与气体入口(节流孔)半径rj为已知，k为气体的绝热指数，则可求出平行圆盘内各点处的马赫数Ma，其计算公式[4]为：

(1)

由式(1)即可求得O点发出第一条膨胀波前不同半径处的Ma分布。

2.1 膨胀波位置的计算

膨胀波位置示意图如图2所示。图2中，μ为O点发出第一条膨胀波的马赫角，δ为壁面转折角，dr和dy分别是轴承径向和气膜厚度方向上的微元段，A1为O点发出的第一条膨胀波上的一点，A为该膨胀波与上壁面的交点。

图2 膨胀波位置示意图Fig.2 Diagram of position of expansion wave

将由O点发出的第一条膨胀波划分成无限多个微元段，每个微元段可看作直线马赫波。不同rx处马赫角不同，微元段OA1可近似为直线马赫波，马赫角μ可由O点的波前马赫数求得，即μ=arcsin(1/Mao)。

由图2可知，dy和dr之间的关系为dy/dr=tanμ。膨胀波不同位置处马赫角μ的值不同，μ值可由所在点的Ma求得，从而得到dr和dy的关系，确定A1点的位置，再根据式(1)即可求出A1点的马赫数。同理，由A1点沿膨胀波依次求解，可得出整条波OA上各点的具体位置及波前参数。

2.2 自然坐标系到特征线网格的转换

为了方便使用特征线法，在此构建特征线网格，推导由自然坐标系s-n向特征线坐标系ξ-η(见图3)的转化过程。取任一函数f，沿η特征线特征参数ξ保持不变，沿η特征线函数变化Δf仅与η有关。图3中，从O到O′的变化可近似写为：

(a)特征线网格 (b)自然坐标系

图3特征线网格和自然坐标系

Fig.3Characteristiclinegridandnaturalcoordinatesystem

(2)

沿流线s可知：

(3)

由式(2)、式(3)可得：

(4)

根据图3右侧自然坐标系的坐标几何关系，可将式(4)变换为：

(5)

同理可得ξ方向的导数：

(6)

2.3 普朗特-迈耶流动中相容关系式的推导

笛卡尔坐标系下普朗特-迈耶(P-M)流动的气体动力学方程为：

(7)

(8)

在自然坐标系s-n下，速度矢量或分量可用速度模和方向(ω，θ)来表示，自变量用流线坐标(s，n)来表示，气体动力学运动方程[9]可表示为：

(9)

(10)

由马赫角μ与马赫数Ma的关系式cotμ=Ma2-1可得：

或

(11)

将式(9)通乘tanμ，式(10)通乘tanμcotμ，再将式(11)代入可得：

(12)

(13)

将式(12)、式(13)相加、相减分别得：

(14)

(15)

令f=ν-θ和f=ν+θ，并分别将式(5)、式(6)代入，则式(14)、式(15)可变为：

(16)

(17)

式(16)、式(17)是P-M流动的气体动力学方程在特征线坐标系下的表达形式，它们给出一个简单的结果：函数ν-θ和ν+θ分别在η特征线和ξ特征线上不变。Liepmann[9]将函数ν-θ和ν+θ定义为黎曼不变量。

2.4 柱对称流动中相容关系式推导

自然坐标系下柱对称流动气体动力学方程为[9]:

(18)

(19)

比较式(9)和式(18)可以看出，二维平面流动与柱对称流动控制方程的差别在于sinθ/r项。特征线坐标系下柱对称流动控制方程的推导过程与前述P-M流动中的推导过程类似，在此不作赘述，直接由方程式(18)、式(19)写出在特征线坐标系下柱对称流动的相容关系：

(沿η)

(20)

(21)

3 特征线法求转折点后的流动参数

特征点网格位置如图4所示，转折点为点1，并将点1设置为坐标原点。转折点处半径为r1(即rO)。气流方向角θ定义为气流方向与圆盘轴线的夹角。轴承径向与轴线夹角为90°，即1点处气流方向角θ1为90°。在图4中，从1点绕A点顺时针旋转，角度θ减小，反之则θ增大。壁面转折角δ定义为轴承壁面与径向的夹角，由图4可知δ角为负值，1′点绕O点顺时针旋转，δ值减小，反之增大。由于篇幅所限，本文只讨论单壁面无膨胀波反射情况。

图4 特征线网格位置示意图Fig.4 Diagram of position of characteristic grid

3.1 壁面点参数的求解

在求得平行圆盘间隙各点参数后，由前述关于膨胀波位置的计算方法可求出从转折点O处发出的第一条特征线上的参数，即图4中点1～5的参数。接着求解经转折点膨胀后特征线上的参数。首先求解壁面点参数。已知点2参数以及壁面偏转角度δ(见图5)，从点2发出的特征线交壁面于点1′，待解点1'的位置由几何位置关系决定。

图5 壁面点求解示意图Fig.5 Diagram of solution of wall point

由边界条件可知，点1′处的气体流动方向与壁面平行，其参数由特征线坐标系下的相容关系得到。具体解法如下：

线ξ21′的斜率为：

(22)

其点斜式方程为：

(23)

整理得其直线方程为：

(24)

转折壁面的斜率为：

k=tanδ

(25)

转折壁面的点斜式方程为：

(26)

整理得其直线方程为：

y=xtanδ+yO-xOtanδ

(27)

联立式(24)、式(27)便可求解出1′点的位置坐标。

由两点间的距离公式可得，2点到1′点的距离为

(28)

再由边界条件计算出沿壁面流动的角度：

θ1′=θ1+δ

(29)

从2点到点1′沿特征线ξ由相容关系式(21)可得：

(30)

将式(30)右端括号内的量近似为常数，且具有点2的已知值，积分得：

(31)

无论在自然坐标系还是特征线网格中，ν、μ均为马赫数Ma的函数，由普朗特-迈耶方程可知其关系为：

(32)

求解方程组式(29)、式(31)可以得到点1′处的ν1′和θ1′。再将ν1′代入式(32)，用二分法可以求出1′点的马赫数Ma1′，进而求得：

μ1′=arcsin(1/Ma1′)

(33)

3.2 内部点参数的求解

内部点的处理是指由不在同一条特征线上的两个已知点求解出这两条特征线相交点的参数。如图6所示，点3和点1′不在同一特征线上，点3顺流而下发射出的特征线ξ与点1′发射出的特征线η交于点2′，已知点3和点1′的参数，则点2′参数可联立两相容方程求解，其位置由特征线方向所决定。下面求其数值解。

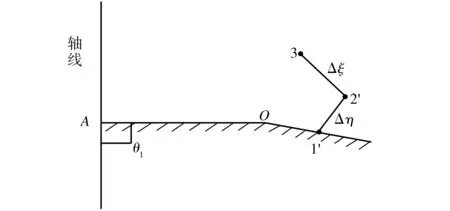
图6 内部点求解示意图Fig.6 Diagram of steps of solution of the interior point

由特征线性质可知，特征线ξ32′的斜率为：

(34)

点斜式方程为：

(35)

直线方程为：

(36)

特征线η1′2′的斜率为：

(37)

点斜式方程为：

(38)

直线方程为：

(39)

联立方程式(36)、式(39)可以给出待解点2′的位置坐标(x2′,y2′)。

求解出以上各点位置，再求沿特征线变化的距离：

(40)

(41)

在特征线网格下利用特征线法求解2′点参数，由点3到点2′的关系式为：

(42)

从点1′到点2′的关系式为：

(43)

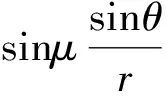
(44)

在式(43)中，μ、θ、r值为点1′的参数，可将其积分为：

(v2′-θ2′)-(v1′-θ1′)=

(45)

联立式(44)、式(45)可得：

(46)

(47)

从而可以求出点2′的参数ν2′和θ2′。由式(32)、式(33)求出μ2′。

4 算例分析

为验证本计算方法的可行性，将此法应用于P-M流动，并与P-M流动理论的计算结果进行比较。

算例：一个马赫数为1.4的均匀空气(绝热指数k=1.4)绕外凸壁膨胀，气流逆时针方向转折不同角度(1°～80°)时，计算膨胀波后的最终马赫数。

分别用P-M流动理论和本文的特征线法对单壁面无膨胀波反射的二维流动进行求解，求解时用Fortran 90编程，用Matlab绘制成可视图，如图7所示。从图7中可知，采用特征线法的计算结果与P-M流动理论值相吻合，表明本文计算方法是可行的。

图7P-M流动理论和特征线法计算结果

Fig.7ResultsofcalculationbyPlantMayerflowtheoryandthecharacteristicmethod

5 结论

(2)将二维无旋超音速流转化到特征线坐标系下，引入Liepmann定义的黎曼不变量后，方程形式简洁，边界条件的处理直观易懂。

(3)将特征线坐标系下的特征线方法应用于圆盘气体轴承中柱对称径向流单壁面膨胀波的计算，计算方法具有可行性。

[1] Harada H,Tsuno K.Study of a disk MHD generator for nonequilibrium plasma generator(NPG) system[J]. Energy Conversion and Management,1998, 39(5):493-503.

[2] Okamura T,Okuno Y. Performance of disk MHD generator with high magnetic flux density[J]. Energy Conversion and Management,2001,42(7):855-866.

[3] Ishikawa M,Matsuo T. Stability analysis of MHD disk generators and application to power systems with CO2recovery[J].Energy,1997, 22(2-3):239-247.

[4] 郭良斌，彭宝林. 理想气体条件下平行圆盘止推气体轴承承载力特性研究[J].武汉科技大学学报,2011,34(1):62-68.

[5] 王祖温，孙昂.静压气体轴承超声速现象的研究与发展[J].机械工程学报，2006,42(1):6-10.

[6] 童秉纲，孔祥言，邓国华.气体动力学[M].北京:高等教育出版社,2012.

[7] M·J·左克罗, J·D·霍夫曼.气体动力学[M] .王汝涌，吴宗真，吴宗善，等译.北京:国防工业出版社,1984.

[8] Courant R,Friedrichs K O.超声速流与冲击波[M]. 李维新，徐华生，管楚洤，等译.北京:科学出版社,1986.

[9] Liepmann H W,Roshko A.Elements of gasdynamics[M].California:California Institute of Technology，1957.