基于局域均值分解的轧制力响应频率提取

金晓宏，樊 捷

(武汉科技大学机械自动化学院，湖北 武汉，430081)

轧件表面的响应如轧制力的大小、频率等信息是轧制过程控制的重要参数，而响应频率中的基频大小是轧制过程各控制元件时间常数选择和分配的重要依据。因此，准确获取轧制力响应频率信息，对避免由于响应不足而导致的轧制力数值采样不足十分重要。由于轧制力传感器通常无法安装在轧件表面，而是安装于辊系轴承座与牌坊之间，因此，其响应是轧件表面响应与辊系响应之差；将辊系响应从轧制力传感器响应中分离出去，留下的信息即为轧件表面响应信息。轧制力传感器信息中，综合响应频率的基频和三倍频数值的提取是其重点和难点。

目前，对于响应基频信息提取方法的研究主要集中于声学信号的相关研究[1-3]上，所利用的方法也主要是基于小波分析提出的一些算法[4-5]。小波分析虽然具有一定的时频分析能力，但由于选取小波基的难度，信号提取结果上很难达到满意的效果。而在机械实测信号响应频率提取方法的研究中，多数研究只提取了频率信息却未具体分析频率信息的含义[6-8]；还未见有对多组实测信号综合频率响应的分析。

近年来，出现了许多先进的信号分析方法，其中局域均值分解方法(Local Mean Decomposition, LMD)[9]实质是将一个多分量信号分解为若干个瞬时频率有物理意义的乘积函数(Production Function，PF)，每一个PF分量是一个包络信号和一个纯调频信号的乘积，包络信号是该PF分量的瞬时幅值，而分量的瞬时频率可以由纯调频信号求出，根据PF分量的这一本质，就可以得到信号在不同频段的频率分布，从而提取出信号的频率参数。本文研究利用局域均值分解法对多组轧制力信号同时进行特征频率提取的方法，并将其应用于实际生产中轧制力信号的提取中，以得到轧制力传感器响应基频和三倍频的值。

1 局域均值分解

局域均值分解的基本步骤如图1所示。首先，确定原始信号x(t)的所有局部极值点。LMD

图1LMD分解基本步骤

Fig.1LMDbasicsteps

分解的一个重要步骤是用滑动平均方法求取函数表示，包络线的幅值则用局域包络函数表示，找出信号的极值点后，任意2个相邻极值点之间局域均值即为极值点的平均值，第i段的局域均值函数mi由下式给出：

mi=(ni+ni+1)/2

(1)

式中：ni、ni+1为相邻极值点。

在信号的极值点，局域均值函数定义为左右两点的均值。同样第i段局域包络函数ai为相邻极值点之差，即

ai=|ni-ni+1|/2

(2)

将ai与mi作滑动平均，跨度为相邻极值点最长距离的1/3，设函数的初始值为y(i) (i=1, 2, 3,…,p)，其中p为该序列的元素个数。按下式计算ai与mi滑动平均的值：

ys(i)=

(3)

式中：N为y(i)到滑动起点的距离。

式(3)中，2N+1为滑动跨度。2N+1必须为奇数，因为若为偶数，代入式(3)可以发现，分子中会漏算y(i)这一极值点，因此，若2N+1为偶数则减去1。

如果在滑动平均之后，还有相邻点的值相等，则继续对求得的结果作滑动平均，直到相邻两点不相等为止。

求出x(t)的局域均值函数m11(t)和局域包络函数a11(t)之后，将m11(t)从x(t)中分离出来，得到：

h11(t)=x(t)-m11(t)

(4)

再将h11(t)以a11(t)进行解调，得到：

s11(t)=h11(t)/a11(t)

(5)

理想地，s11(t)是一个纯调频信号，即其包络函数恒等于1。若不满足此条件，则对s11(t)重复上述迭代过程，直至s1n(t)成为一个纯调频信号。

最后将迭代所产生的局域包络函数相乘得到PF分量的包络信号：

(6)

将包络信号a1(t)与纯调频信号s1n(t)相乘即可得到第一个PF分量：

PF1(t)=a1(t)s1n(t)

(7)

将x(t)减去PF1(t)，得到一个新信号，再将新信号作为原始数据重复上述步骤k次，直至分离后信号的极值点不大于1为止，此时剩余函数为uk(t)，即

(8)

其中，p为PF分量的序号，uk(t)是残余项，PFp(t)为包络信号和纯调频信号的乘积，即

PFp(t)=ap(t)sp(t)

(9)

2 基于Hilbert变换的瞬时频率计算方法

信号x(t)的Hilbert变换定义如下[10-11]：

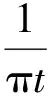
(10)

对于离散信号，Hilbert变换可以定义为一个全通滤波器的形式：

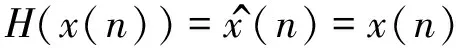
*h(n)

(11)

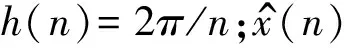
同样，信号相位的计算公式为：

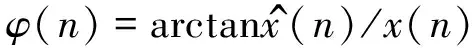
(12)

计算瞬时频率采用差分公式，计算式为：

ω(n)=φ(n)-φ(n-1)

(13)

3 计算方法的有效性验证

记测试信号x(t)=sin(10.5×2πt)+sin(43.5×2πt)+ sin(102.3×2πt)，取其采样频率fz=1024 Hz，点数N=256，t∈[0,0.25]。测试信号曲线如图2所示。

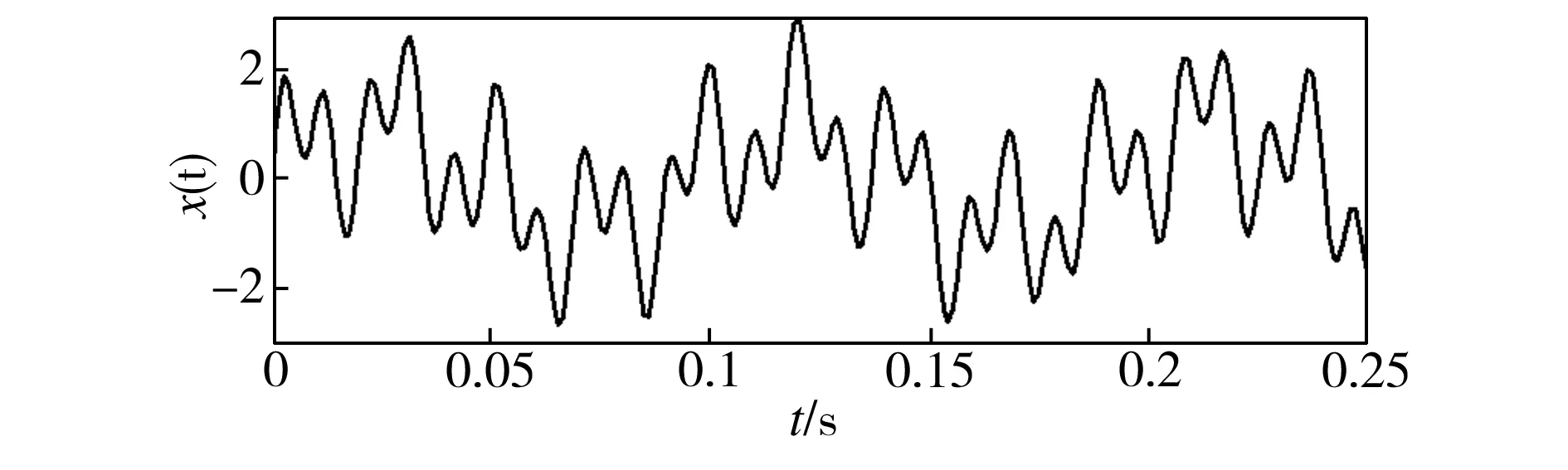
图2 测试信号曲线Fig.2 Curve of the test signal

图3所示为测试信号的LMD分解结果。测试信号经过分解，变成了3个周期信号PF1、PF2和PF3，表明原信号是由3个周期信号叠加而成。进一步求取这3个信号的瞬时频率，利用其频率值来验证本文瞬时频率计算方法的有效性。

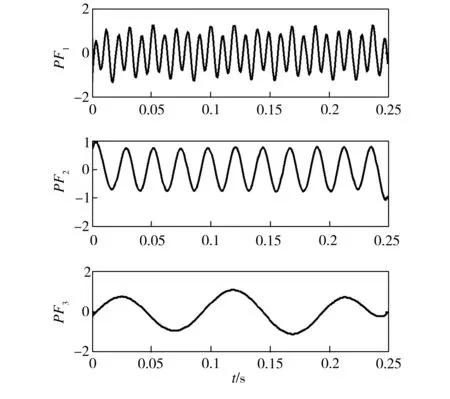
图3 LMD分解结果Fig.3 Results decomposed by LMD

利用Hilbert变换求解各PF分量的瞬时频率，结果如图4所示。

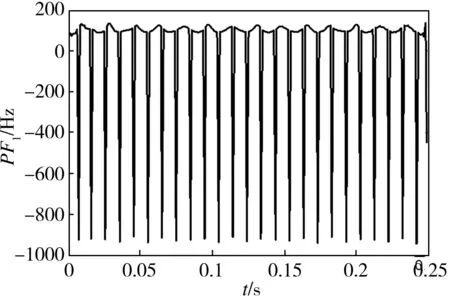
(a)PF1

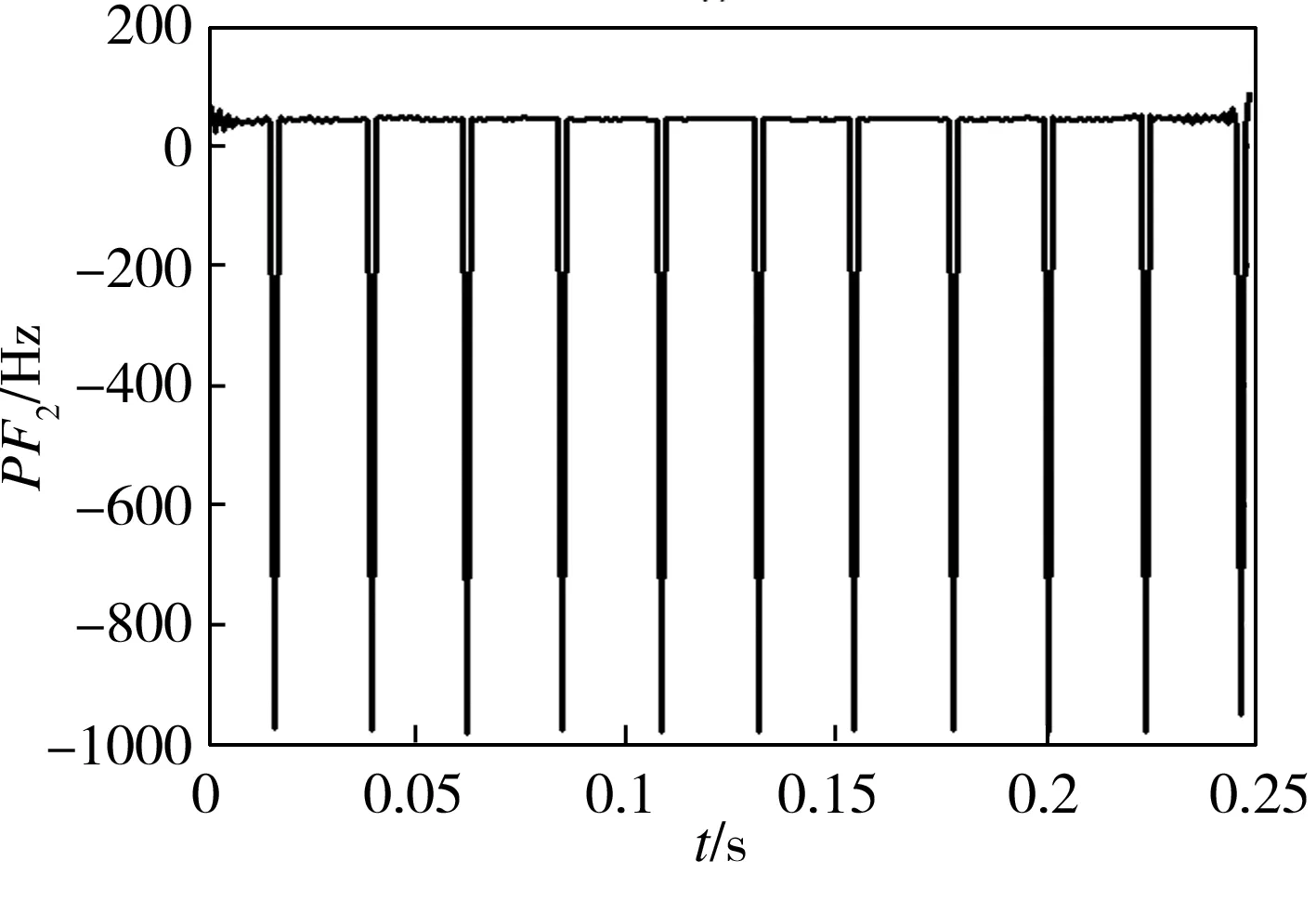
(b)PF2

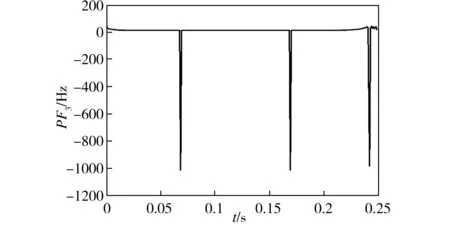
(c)PF3

从图4中可以看出，计算结果中出现了很多毛刺，即“负频率”。这些毛刺的出现是因为讨论的基准是以复指数信号为正交基展开的，正弦信号在复指数信号为正交基的无穷维空间中，可以展开为两个复指数信号的和，分别是正频率和负频率，负频率没有实际的物理意义，可将其剔除并用相邻点的均值代替。图5所示为测试信号经LMD分解后各PF分量去除毛刺后的瞬时频率。

图5中，虚线标出了各分量主要频率所处的频带。由图5中可以看出，求得的瞬时频率有明显的端点效应，在低频部分特征频率更为明显，3个PF的瞬时频率分别为位于90～120 Hz、37～42 Hz和8～12 Hz的频带，且频率均值分别为102.0549 Hz、43.6091 Hz和10.5163 Hz。对于频率分布更为明显的低频部分，精确度达到99.8%。在计算过程中，可以截取时间中段的频率值进行频率均值的求解。

(a)PF1

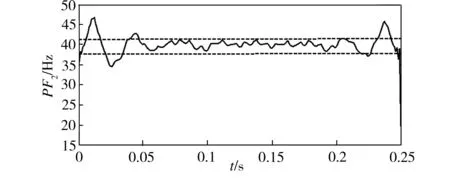
(b)PF2

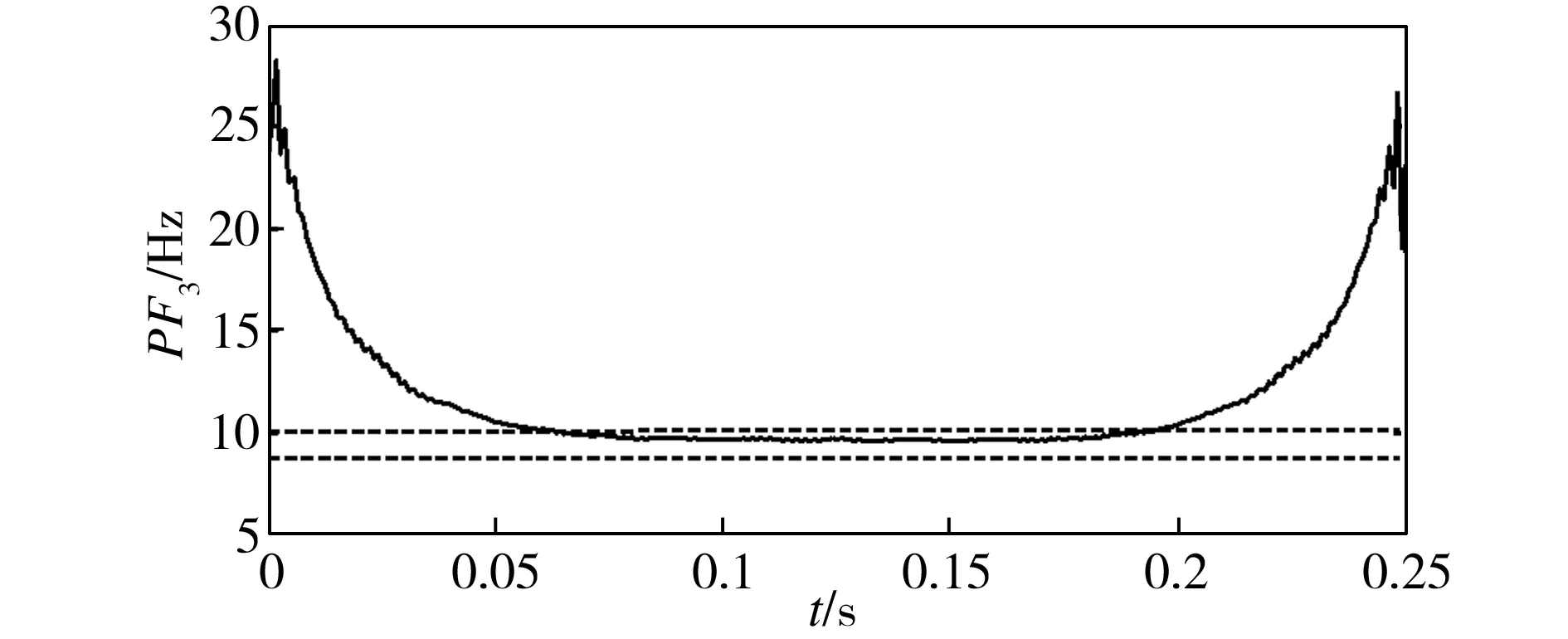
(c)PF3

Fig.5ThreecomponentsofPFfortestsignal’sinstantaneousfrequency

将测试信号进行傅立叶变换，结果如图6所示。由图6中可以看出，原信号中确实含有102.3Hz、43.5 Hz和10.5 Hz的特征频率。这验证了本文计算方法的有效性。

图6 测试信号傅立叶变换结果Fig. 6 Fourier transform results of the test signal

根据香农采样定理，信号采样频率应远大于所提取的频率最大值的2倍。前述所提取的频率最大值为102.3 Hz，它的2倍远小于信号采样频率1024 Hz，因此满足香农采样定理，表明所提取的频率值不存在由于混叠引起的频率混杂。因此，将某一信号进行LMD分解，并对得到的PF分量求瞬时频率，得到瞬时频率的均值可以用于表征信号的某一特征频率，且低频成分中，所提取的频率值更为精确。

4 轧制力实测信号的LMD分解及分析

实测信号为直接取自某厂1700 mm五机架冷连轧四辊轧机机组第一机架参与辊缝控制的轧制力传感器采集的实时信号。共采集A、B、C三组数据。轧制条件参数及采样条件如表1所示。

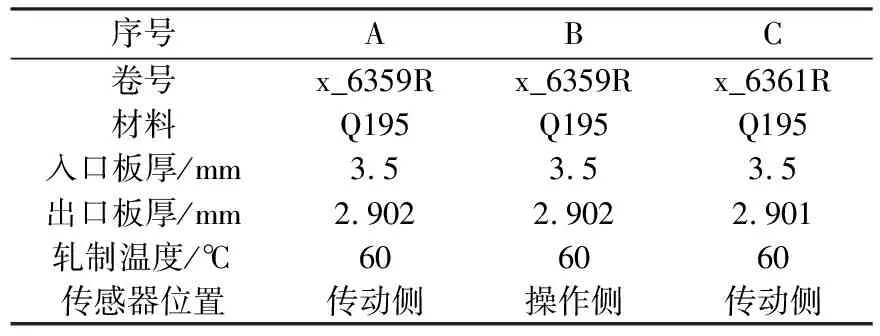
表1 轧制参数Table 1 Rolling parameters

信号的采样频率为250 Hz，根据香农采样定理，提取的最大频率数值应不超过125 Hz。由于A、B两组数据卷号一致，如果两组数据均含有相同的基频，则表明该响应同时存在于同时刻辊系两侧的传感器；而将不同时段的C组数据与A、B组数据处理后进行对比，若基频相同，则表明该响应不止存在于A、B时段内，而是存在于整个轧制过程中。

(1)A组数据。在A组轧制条件下的实测轧制力数据如图7所示。

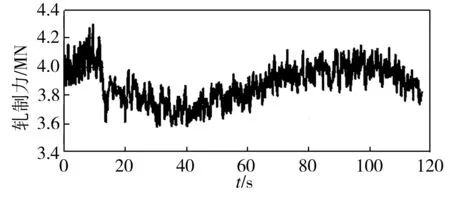
图7 A组实测数据Fig.7 Measured data for Group A

将实测信号进行LMD分解，其结果如图8所示。由图8中可见，从PF1到PF5，信号的振动周期逐渐增大，频率范围依次减小，各个分量可以分别代表原信号在不同频段的频率分布，对其中的第二、三个分量求瞬时频率，其结果如图9所示。图9结果去毛刺后可得PF2和PF3的瞬时频率如图10所示。由图10中可以看出，在整个时间段内，虽然存在许多干扰频率，但第二分量频率主要集中在15～42 Hz频段，其瞬时频率的算术平均值为23.0417 Hz；第三分量频率主要分布在5～18 Hz的频段，能量主要集中在10 Hz左右，其瞬时频率的算术平均值为8.4335 Hz。这表示在测量时段内，信号在这个频率值上能量最强。求得的两个频率值表征了实测信号的两个特征频率。

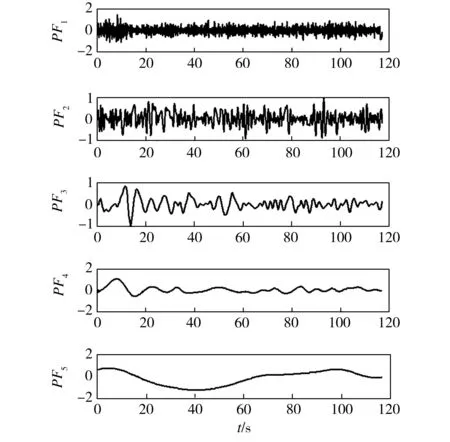
图8 A组信号LMD分解后各PF分量Fig.8 Components of Group A after LMD

(a)PF2

(b)PF3

Fig.9InstantaneousfrequenciesofthecomponentsPF2andPF3(Nodeburring)

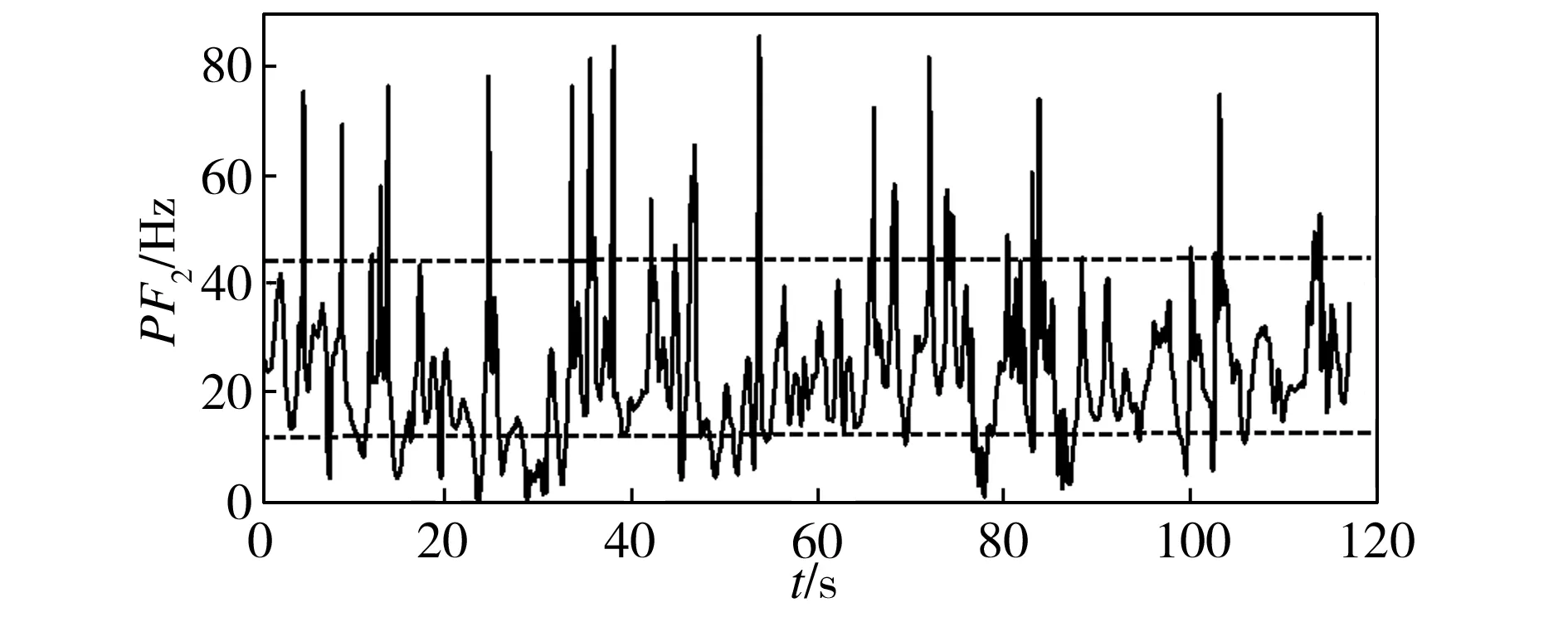
(a)PF2

(b)PF3

Fig.10InstantaneousfrequenciesofPF2andPF3forgroupA(Afterdeburring)

(2)B组数据。该信号具体数据如图11所示。将其进行LMD分解，结果如图12所示。

图11 B组信号实测数据Fig.11 Measured data for Group B

图12 B组信号LMD分解后各分量Fig.12 Components of Group B after LMD

对B组信号的PF2和PF3求取瞬时频率，并去除毛刺，所得的瞬时频率分布如图13所示。由图13中可知，B组第二、三分量瞬时频率的算术平均值分别为24.0642Hz和8.6182 Hz，与传动侧所得的相应频率值23.0417Hz和8.4335Hz接近，且B组第三分量的干扰比A组第三分量的干扰要少。

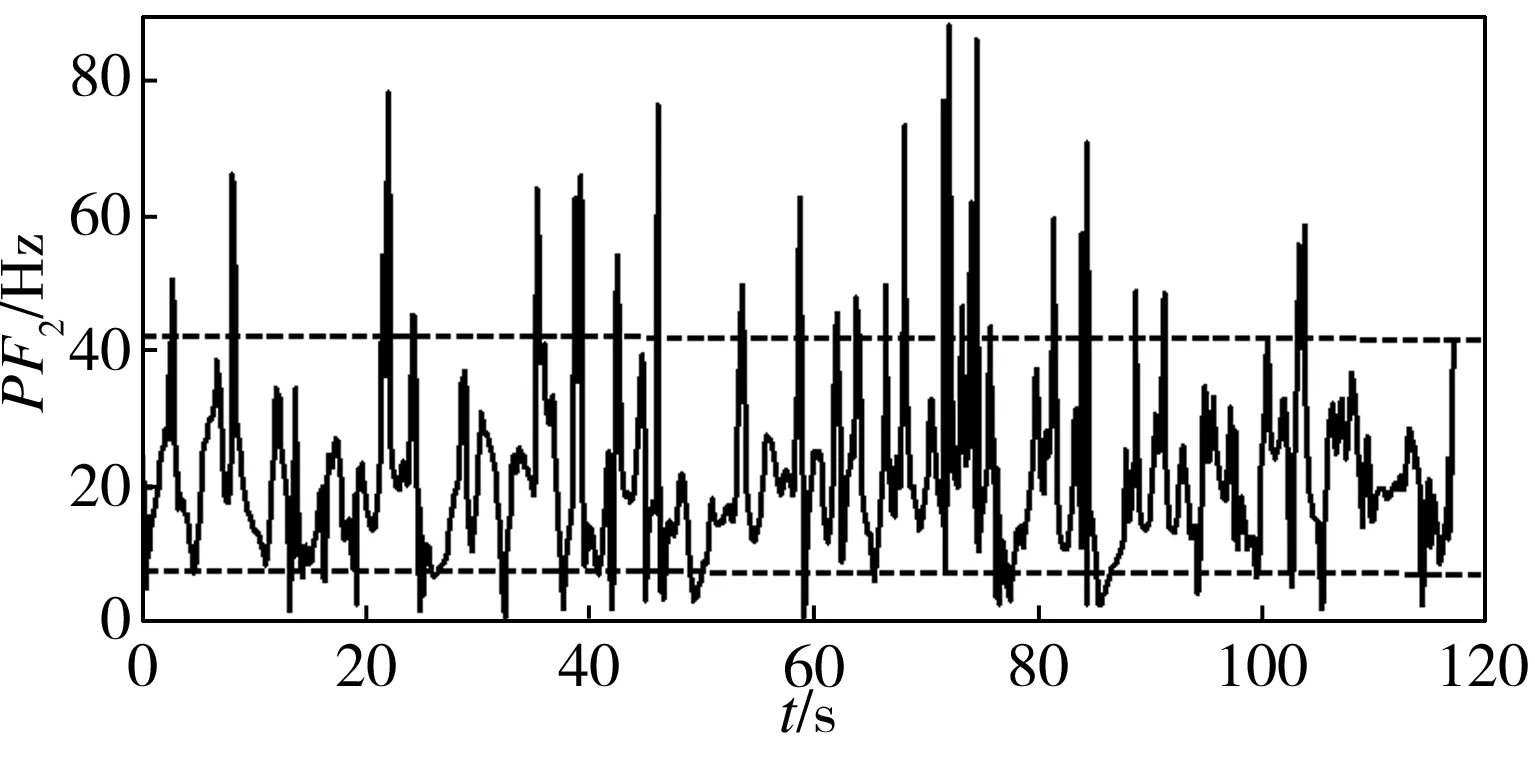
(a)PF2瞬时频率

(b)PF3瞬时频率

Fig.13InstantaneousfrequenciesofPF2andPF3forGroupB

(3)C组数据。C组信号的实测数据如图14所示。将其进行LMD分解，结果如图15所示。对C组信号的PF2和PF3进行瞬时频率求解并去毛刺，结果如图16所示。

由图16中可见，该组数据分解后较前两组数据而言，第三分量少了很多高频部分，主要频率也全部低于40 Hz，干扰更少；第二、三分量瞬时频率的平均值分别为25.4017 Hz和8.4370 Hz，与前两组数据的结果接近。

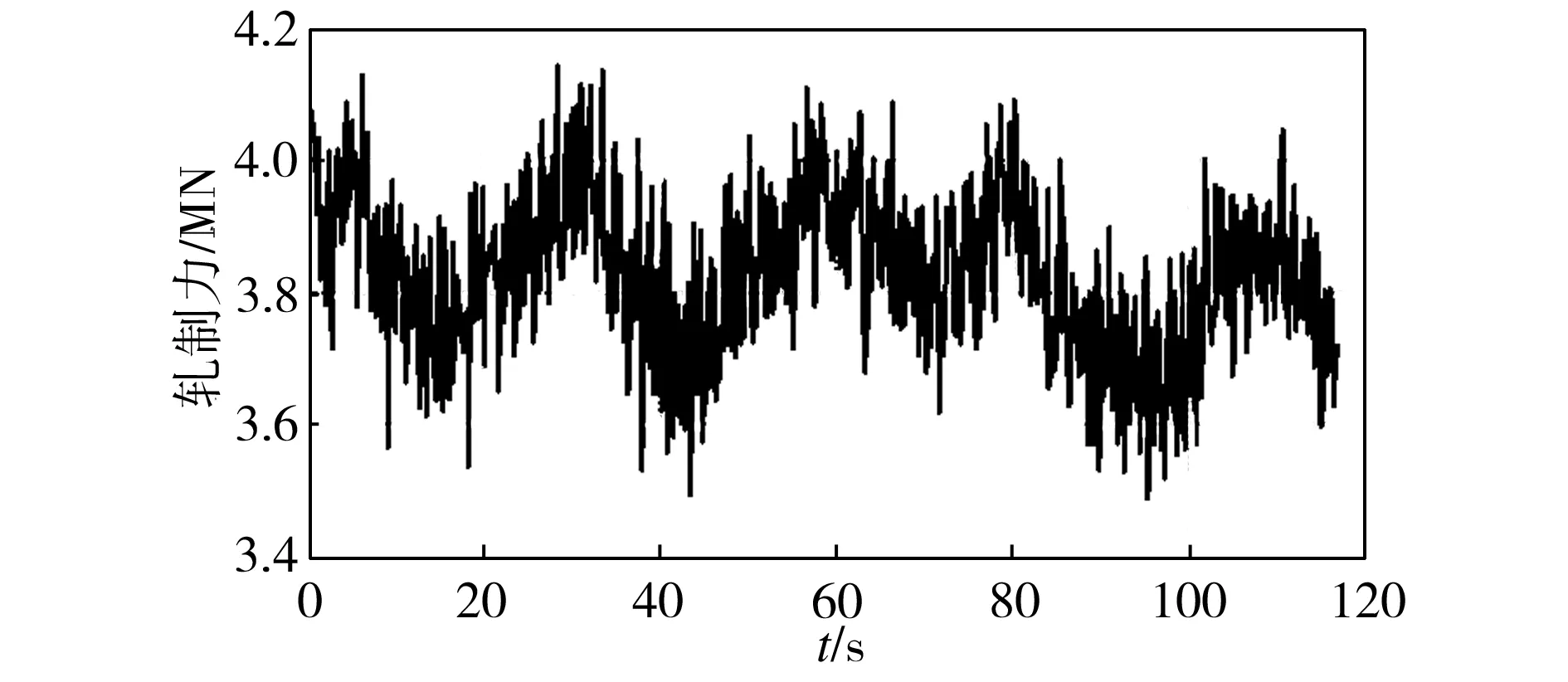
图14 C组信号实测数据Fig.14 Measured data for Group C

图15 C组信号LMD分解后各分量Fig.15 Components of Group C after LMD

(a)PF2瞬时频率

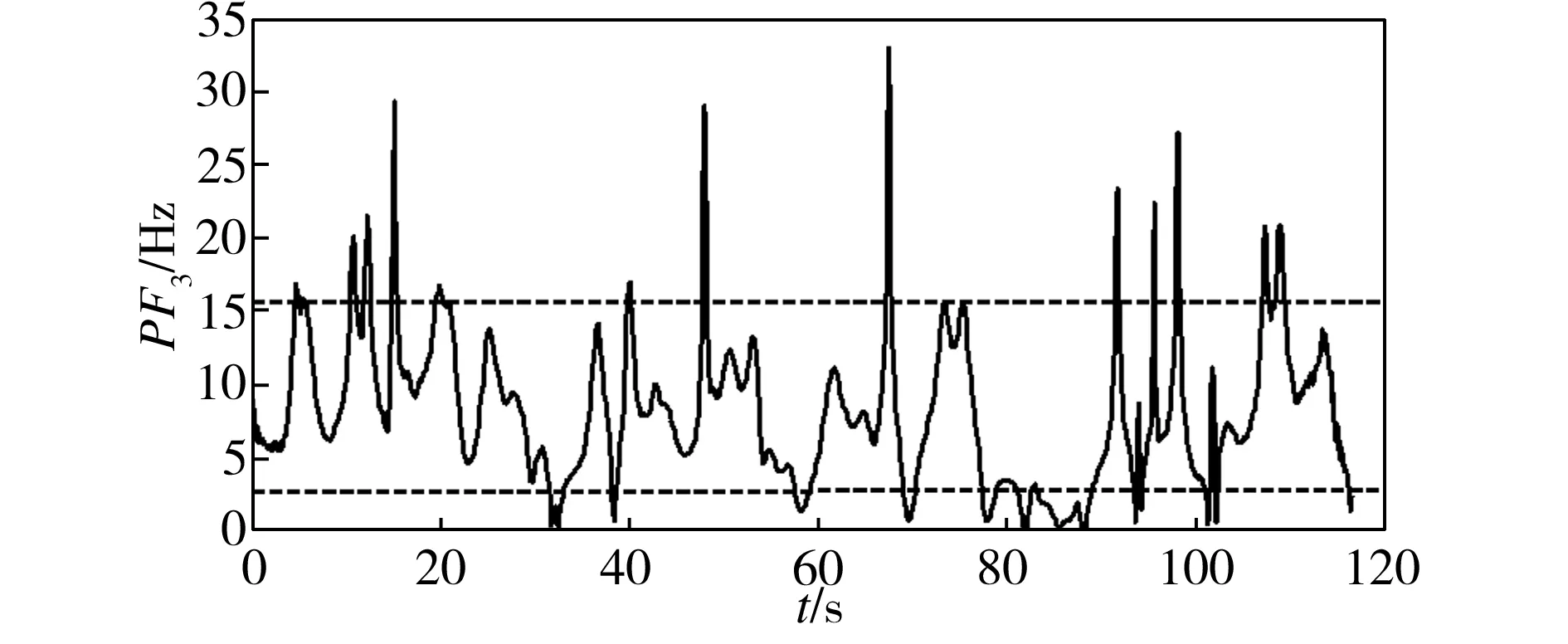
(b)PF3瞬时频率

Fig.16InstantaneousfrequenciesofPF2andPF3forGroupC

从上述3组信号的计算结果中可以看出：

(1)轧制信号中频率越高的频段，信号成分越丰富，干扰信号也越多。

(2)3组信号PF分量的第二、三分量的频率均相近，并且比较第二分量和第三分量的瞬时频率求解结果，明显第二分量的高频成分更多。

(3)3组信号的第二分量频率主要集中于10～40 Hz频带，第三分量频率集中在0～20 Hz频带。3组信号中，始终存在一个8.5 Hz左右以及一个25.4 Hz左右的频率，贯穿于整个轧制过程。多卷信号以同样处理方式能提取到同样的结果，表明整个轧制过程中，有一响应基频8.5 Hz及其三倍频25.5 Hz。

轧制力信号是一个轧机各部件响应的综合体现，轧制力传感器的信号虽然并不是轧制区的真实响应，但由于轧件表面响应传递到轧制力传感器所经过的部件为轧辊、支承辊和支承辊轴承座，这些部件的固有频率远高于100 Hz,因此上述所提取的响应频率基本能表达出轧件表面的响应频率，所提取的8.5 Hz可作为轧制区轧制力响应基频的参考值。

5 结语

本文提出利用局域均值分解的方法处理轧制力信号，将信号分解成不同频段的几个分量，从而求取该信号在不同频段的频率分布，并通过对测试信号的处理验证了该方法的有效性。采用该方法对某厂1700 mm五机架冷连轧四辊轧机机组第一机架参与辊缝控制的轧制力传感器采集的多卷实时信号进行处理和分析，提取出的基频和三倍频分别约为8.5 Hz和25.5 Hz。

[1] 刘海波，李辉，凌震华，等.用于周期分解语音活动检测的基频提取方法研究[J].中国科学技术大学学报,2012,42(2):106-111.

[2] 姚振轩，张效民，赵延安，等.基于基频提取的舰船目标识别系统设计[J].鱼雷技术,2011,19(5):355-359.

[3] 杜雄，王莉萍，李珊瑚，等.一种具有频率响应自适应性的电压同步信号提取方法[J].中国电机工程学报,2012,32(4):115-121.

[4] 董璐，忻蔚然，叶敦范，等. 基于小波变换的音频信号基频提取[J].电声技术,2005(6):50-55.

[5] 钟金宏，杨善林，林逸榕，等. 基于小波变换的语音基频提取新算法[J].电子与信息学报,2002,24(9):1218-1224.

[6] Huang N E, Wu Z H, Long S R.On instantaneous frequency[J].Advances in Adaptive Data Analysis,2009,1(2):177-229.

[7] Loh C H, Wu T C , Huang N E.Application of the empirical mode decomposition Hilbert spectrum method to identify near fault ground motion characteristics and structural responses[J].Bulletin of the Seismological Society of America,2001(5):1339-1357.

[8] 鞠萍华. 旋转机械早期故障特征提取的时频分析方法研究[D].重庆：重庆大学,2011.

[9] Jonathan S Smith.The local mean decomposition and its application to EEG perception data[J].Journal of the Royal Society Interface，2005,2(5)：444-450.

[10]Marcus D, Torsten S. Performance and limitations of the Hilbert-Huang transformation (HHT) with an application to irregular water waves[J].Ocean Engineering,2004(14-15):1783-1834.

[11]任达千，杨世锡，吴昭同，等. 基于LMD 的信号瞬时频率求取方法及实验[J].浙江大学学报:工学版,2009,43(3):523-528.