渗流作用下露天煤矿边坡稳定性数值模拟研究
2014-03-26赵玉成刘家成李敏妙
王 明,赵玉成,2,刘家成,苏 海,李敏妙
(1.中国矿业大学力学与建筑工程学院,江苏 徐州,221116 2.中国矿业大学深部岩土力学与地下工程国家重点实验室,江苏 徐州,221116)
边坡的稳定性是露天矿安全开采的重要保障。因边坡失稳造成的地质灾害严重影响正常的采矿作业,威胁人员和设备的安全,造成巨大的经济损失[1]。复杂的区域构造背景、力学性质薄弱的岩性是导致抚顺西露天煤矿边坡失稳的重要因素,而渗流的作用更不可小觑。抚顺西露天煤矿开采过程中,其生态系统被破坏,地下水及雨水的渗入,一方面会溶解岩体中的部分可溶物质,使土体抗剪能力变差,另一方面水在岩体中运动时会产生渗透力作用在土体上,使边坡岩体发生平面破坏、楔形破坏、圆弧破坏和倾倒破坏,对边坡稳定性造成不利影响。2005年“8·13”强降雨造成抚顺西露天煤矿北帮出现两条巨大的地裂缝,其重要原因之一就是水的作用[2]。
目前,对水的作用下煤矿边坡稳定性研究中,大部分考虑的是水对土体中物质成分产生影响,使土体抗剪能力变差,导致边坡失稳。韩占占[3]曾用Morgenstern-Price法来确定边坡安全系数,为露天煤矿边坡稳定性分析提供科学依据,但其并没有考虑水流动产生的渗流力影响。本文以抚顺西露天煤矿均质土坡为对象,在考虑渗流作用的情况下,利用有限元分析软件ANSYS对露天煤矿边坡的内部应力、位移和安全系数进行研究,以期为预防露天煤矿矿坑的边坡破坏及制定滑坡治理方案提供参考。
1 渗流对边坡失稳的影响
1.1 静水压力的影响
静水压力对岩体性质产生影响。当水向下渗透进入岩体内的空隙和裂隙时,土体含水量增大,土体容重和孔隙水压力也随之增大,而有效应力随之减小,从而引起剪应力的增大和土体抗剪能力的降低。
1.2 动水压力的影响
水在土体中流动时会摇曳土粒而对其稳定性带来不利影响。水流加于土体的力称为渗透力,将单元渗透力分解到直角坐标系中[4]:
(1)
(2)
式中:Px、Py为单元渗透力;h为水头函数;V为单元体积;νw为水的容重;νwV为单元所受的浮力。当坡面有水出流时,水流动产生的渗透力作用于土体,这种力相当于外部施加一种水平推力,使土体内部应力分布发生改变,对边坡稳定性极为不利。
2 露天煤矿边坡稳定性的数值模拟
2.1 数值模型的建立
本文利用有限元分析软件ANSYS对露天煤矿边坡稳定性进行数值模拟分析。抚顺西露天煤矿某均质土坡如图1所示,其坡高为18 m,坡角为53°,土体天然密度为1827 kg/m3,饱和重度为21 kN/m3,黏聚力为25 kPa,内摩擦角为18°,土体孔隙率为0.3。边坡土体等效为各向同性连续介质,其渗透系数为0.14 m/d,弹性模量为30 MPa,泊松比为0.25。
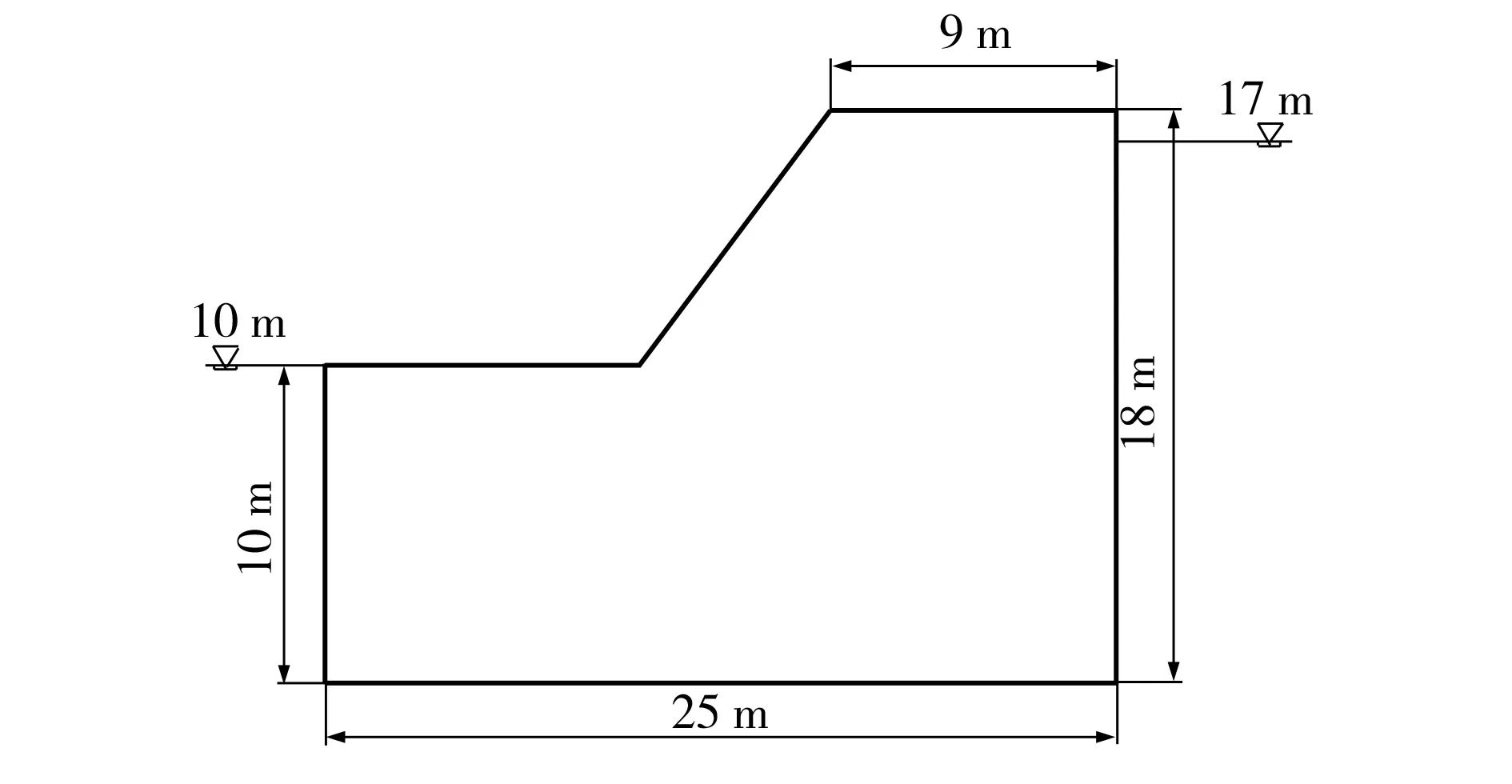
图1 边坡示意图Fig.1 Schematic diagram of the side slope
渗流分析的边界条件为:区域底面为不透水面,边坡表面为可能逸出面边界,右侧施加17 m水头,左侧施加10 m水头。稳定计算边界条件为:左右两侧水平约束,下部固定,上部为自由边界。
为了进行对比分析,本文同时还建立了没有施加渗流力的有限元模型。
2.2 数值模拟与分析
2.2.1 自由面的确立和水力坡降分布规律
均质边坡由于水头差的存在而产生稳态渗流场,渗流场对边坡的应力场和位移场都有很大的影响。在进行渗流场分析时采用整体建模方式。由于自由面上下的渗透系数不同,故首先采用改进的单元渗透系数调整法来迭代计算求解自由面,然后选择单元属性为平面四边形四结点单元(plane55),一次性划分所有单元,并赋予不同的材料属性,最后进行求解。
通过改进的单元渗透系数调整法得到的边坡自由面如图2所示。边坡的渗流量分布如图3所示。结合图2和图3可以看出,自由面以上的区域没有渗流场,在自由面上总水头保持不变,自由面以下是渗流场分布区域,计算得到浸润面逸出点的坐标为(13.36,14.48)。由图3还可以看出,在坡脚处渗流量非常集中,易引起流土现象。
在渗流场中定义一条路径P1,将水力坡降值映射到这条路径上,如图4所示。
路径P1上的水力坡降值如图5所示。由图5可以看出,路径P1上的水力坡降分布规律是:沿着渗流的方向水力坡降值逐渐增大,即越接近坡脚处,水力坡降值越大。由此可推知,当发生渗流滑坡时最容易从坡脚处开始破坏,然后才会慢慢扩展到整个边坡。因此,在防止边坡滑移时,对坡脚部分进行处理是一种行之有效的措施。
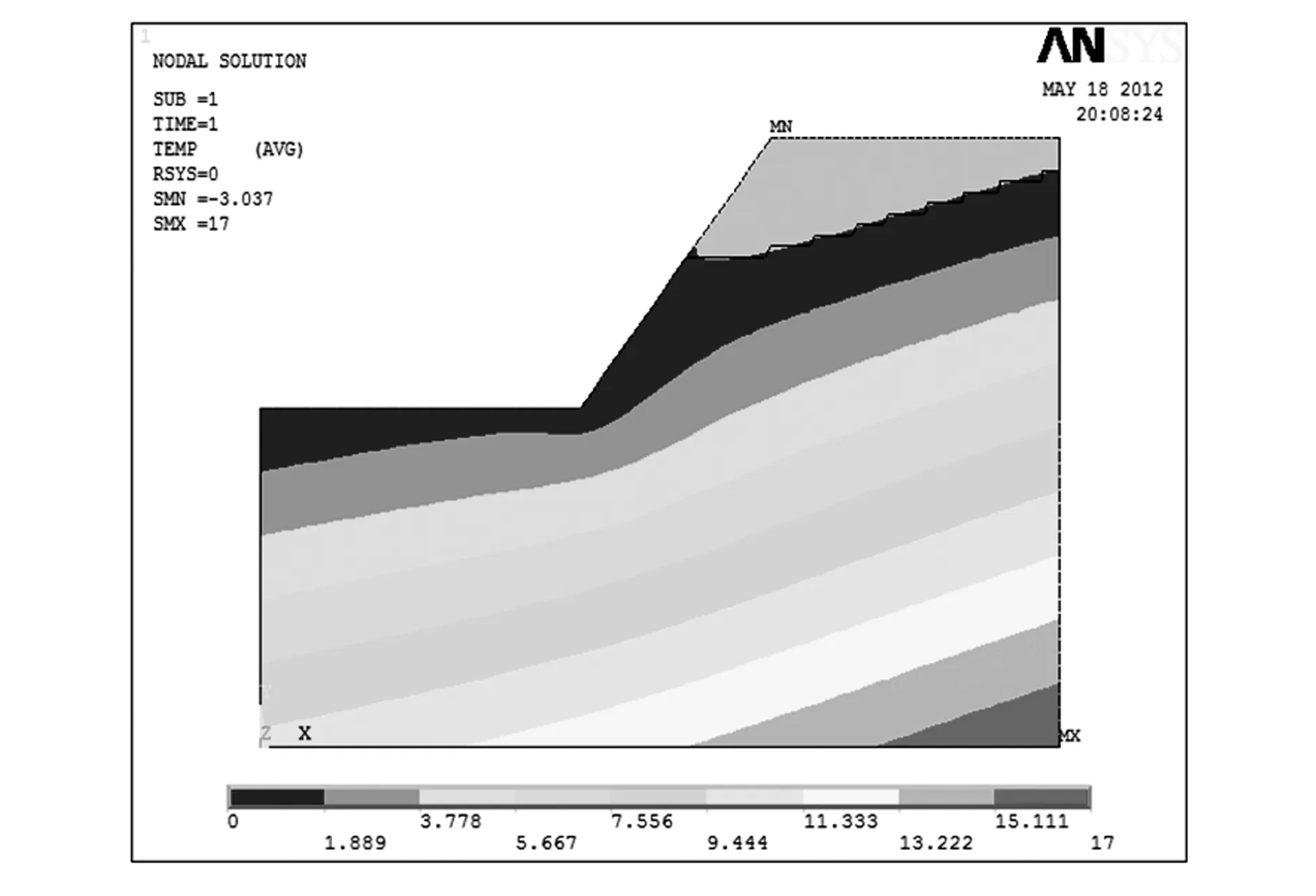
图2 渗透压分布图Fig.2 Distribution contour of osmotic pressure

图3 渗流量分布图Fig.3 Distribution contour of seepage flow

图4 路径P1Fig.4 Route P1
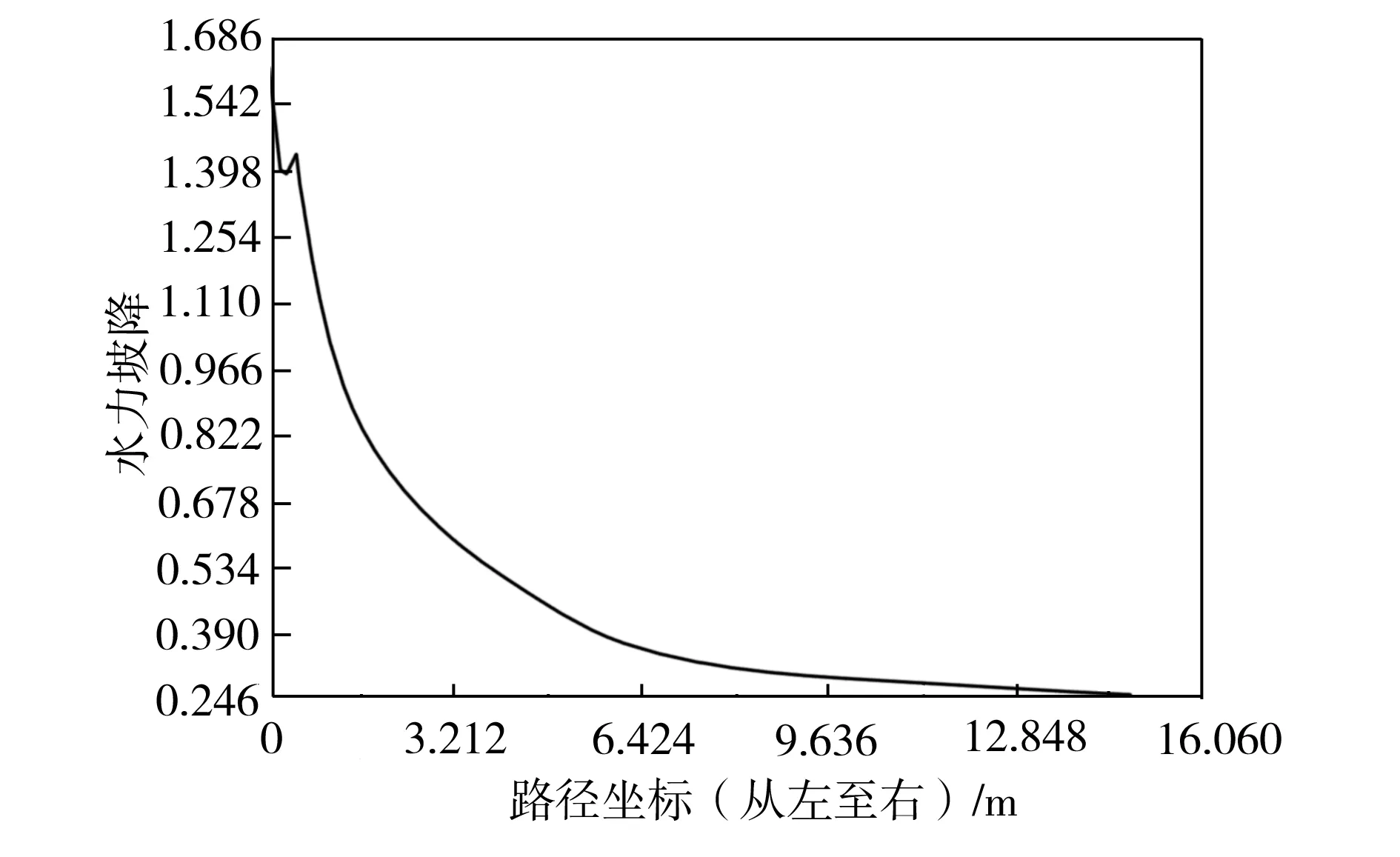
图5 路径P1上的水力坡降Fig.5 Hydraulic gradient on route P1
2.2.2 边坡的内部应力和位移
用ANSYS完成渗流场分析后,通过后处理程序可以求得单元(本文取四节点单元)上各节点的水头梯度值,根据式(1)和式(2)进而可求得单元上的平均渗透力,将单元渗透力转化为等效结点荷载来分析,实现渗流场和应力场的间接藕合,获得边坡的各种应力分布情况。图6为有渗流和无渗流两种情况下的边坡切应力τxy分布云图。
由图6可知,渗流场使边坡应力场得以重新分布,在自由面以下存在渗流,应力场发生很大的变化;在自由面以上无渗流,应力场变化不大。从τxy云图中还可以看出,在无渗流和有渗流两种情况下,坡脚处都存在很大的剪应力,此处最容易产生剪切破坏。
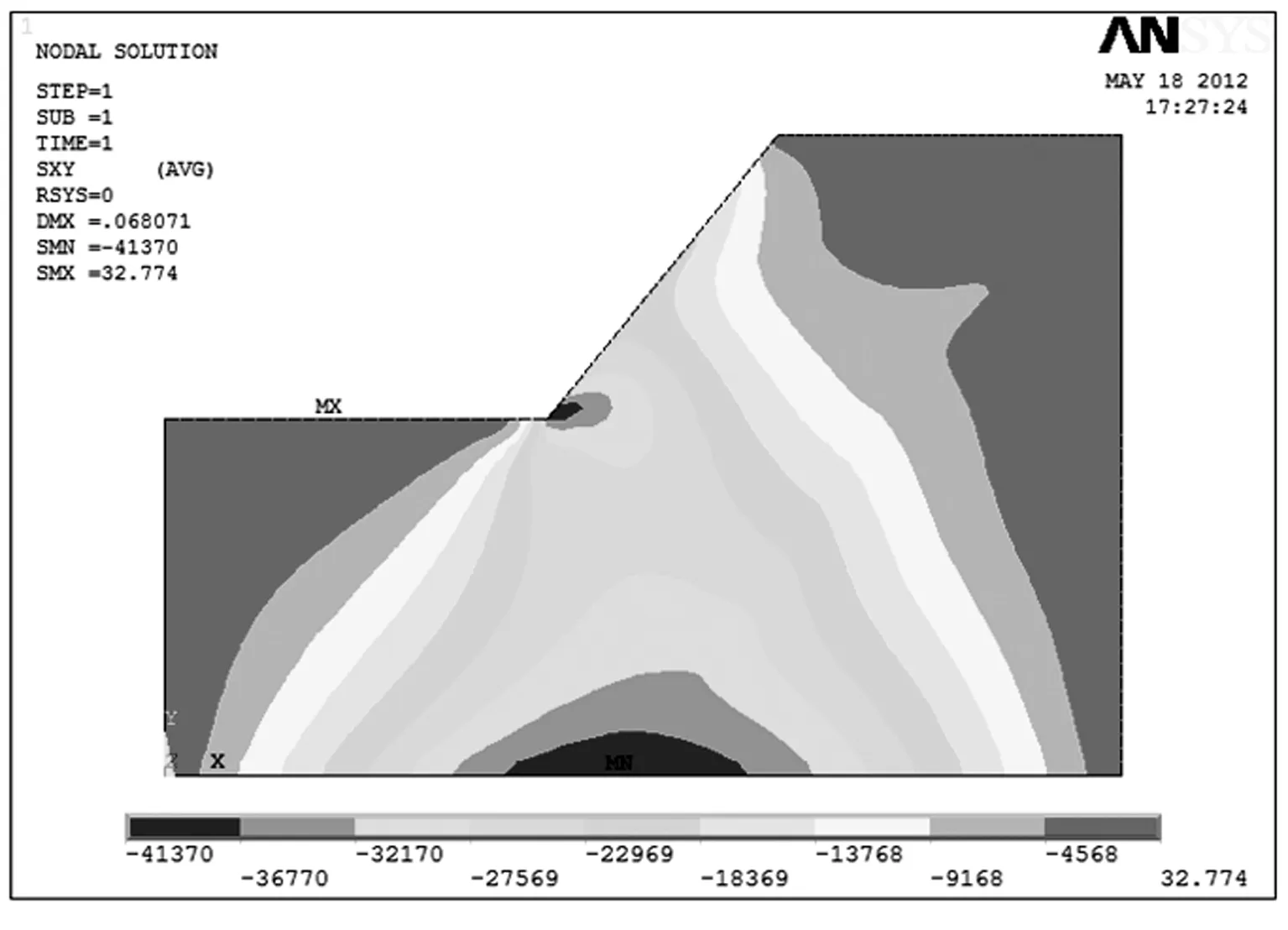
(a)有渗流
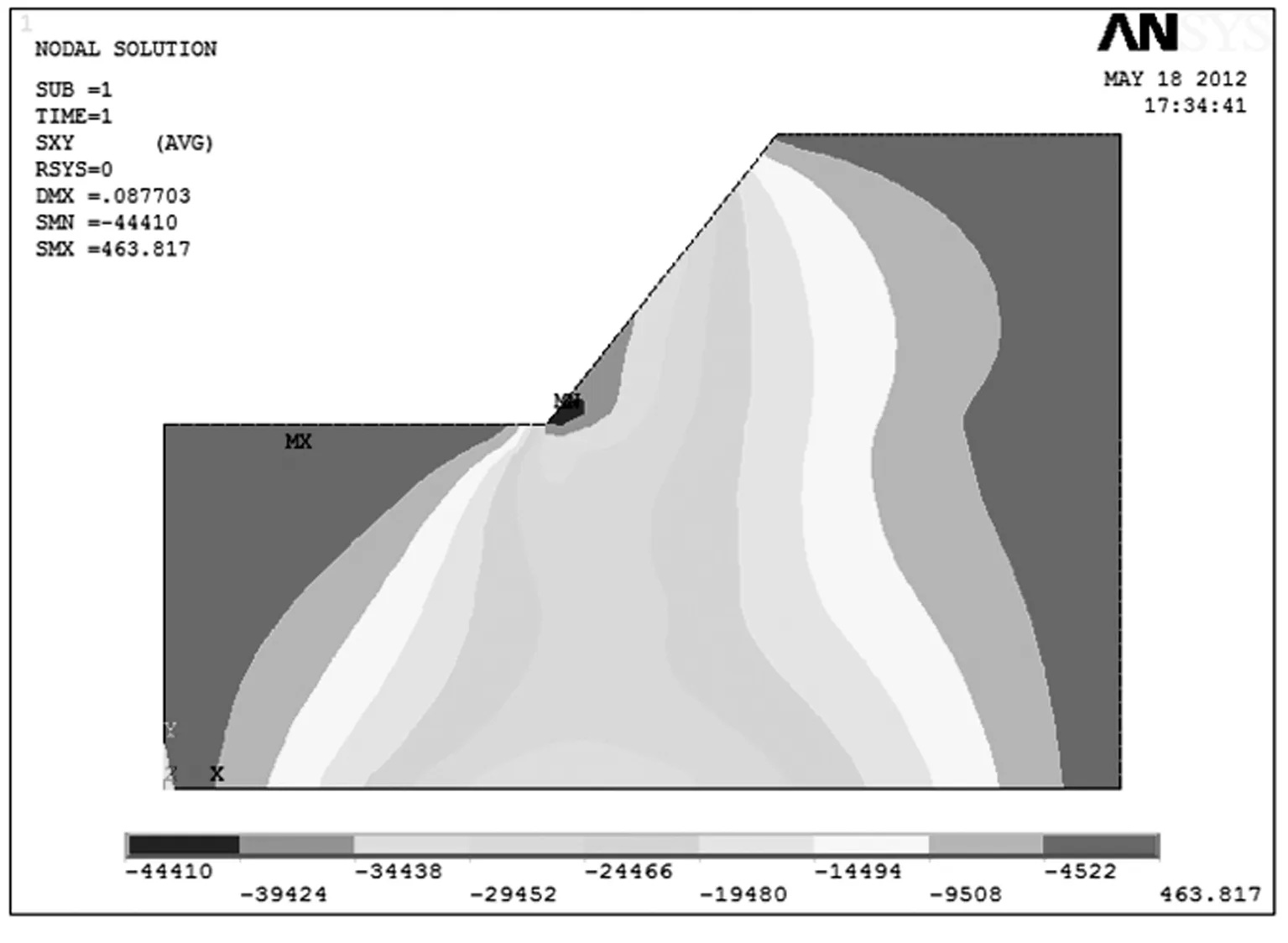
(b)无渗流
图6边坡切应力τxy分布云图
Fig.6Shearstressdistributioncontoursofthesideslope
位移的大小直接反映边坡变形与破坏的趋势,通过ANSYS强大的后处理功能可以得到两种情况下的边坡位移,如表1所示。
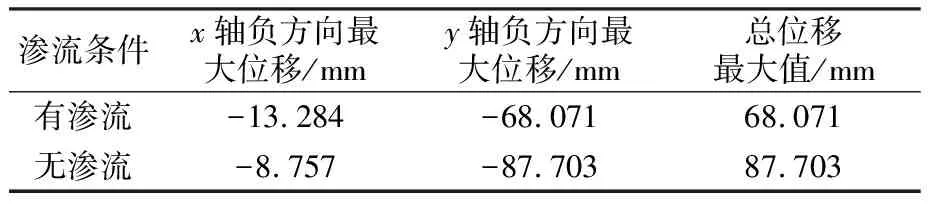
表1 边坡位移Table 1 Displacement of the side slope
由表1可见,沿x轴负方向,有渗流作用下的位移比无渗流作用下的位移大得多,产生这种差异的主要原因是渗流作用使土体受到沿x轴负方向的附加力;沿y轴负方向,有渗流作用下的位移总体上要比无渗流作用下的位移小,这是由于渗流使土体产生向上的附加力的作用结果;从总位移上来看,两种情况下的最大总位移都与y方向最大位移一致,这是由于最大位移点处受x方向约束。
2.2.3 边坡的安全系数
边坡的安全储备能力大小直接影响着边坡的稳定性。本文在求解边坡安全系数时利用ANSYS 12.0提供的岩土非线性弹塑性模型,模型遵循Druker-Prager屈服准则,剪胀角ψ′=0,即没有体积膨胀。用强度折减有限元方法[5]进行计算,求得:有渗流作用下边坡的安全系数Fs=1.609,临界收敛时的等效塑性应变如图7所示;无渗流作用下边坡的安全系数Fs=1.902,临界收敛时的等效塑性应变如图8所示。
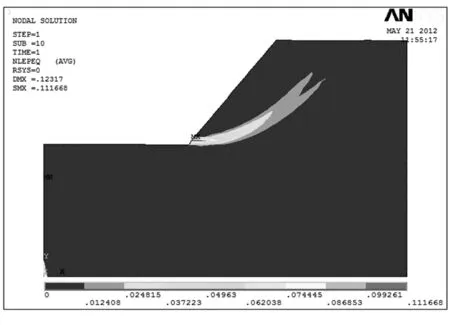
图7 渗流作用下Fs=1.609时的边坡等效塑性应变云图
Fig.7EquivalentplasticstraincontourofthesideslopewithseepagewhenFs=1.609

图8无渗流作用下Fs=1.902时的边坡等效塑性应变云图
Fig.8EquivalentplasticstraincontourofthesideslopewithoutseepagewhenFs=1.902
虽然图7中的边坡等效塑性区域没有贯通,但是当取Fs>1.609时ANSYS计算不收敛,所以有渗流作用下边坡的安全系数还是确定为1.609。
通过有限元强度折减法和等效塑性应变云图,可找出准确的边坡滑移面并得到滑移面的稳定安全系数。在边坡存在渗流的情况下,土的抗剪能力变差,加上渗透力作用于土体,使其容易遭到破坏,安全系数下降。
3 结论
(1)对于富水地区的露天煤矿,水的渗流使边坡稳定性下降,边坡更容易被破坏。由于坡度等原因,本文研究的边坡模型主要以平面破坏为主。
(2)与无渗流情况相比,渗流作用使边坡自由面以下的应力场发生很大变化,而自由面以上的应力场变化不大。
(3)在无渗流和有渗流两种情况下,坡脚处都存在很大的剪应力,此处最易产生剪切破坏,然后慢慢向上扩展,最终贯通到顶部。在防止边坡滑移和土流失时,对坡脚部分进行处理是一种行之有效的措施。
(4)通过有限元强度折减法和临界状态时的等效塑性应变图可得到边坡滑移面及滑移面的稳定安全系数,为制定滑坡治理方案提供科学依据。
[1] 赵锡刚.露天煤矿边坡地质灾害及其影响因素分析[J].现代矿业,2013(1):61-63.
[2] 刘大勇,宋建潮,王恩德.水对抚顺西露天煤矿边坡失稳的影响[J].采矿工程,2007(6):22-24.
[3] 韩占占.哈尔乌素露天煤矿边坡稳定性分析[J].露天采矿技术,2013(9):24-27.
[4] 娄潇聪,黄成,娄一青,等.渗流作用下边坡稳定有限元分析[J].水电能源科学,2008,26(3):57-60.
[5] 秦帆,王正中.基于有限元强度折减理论的边坡稳定分析方法探讨与改进[J].水利与建筑工程学报,2012,10(1):43-47.
