ZPW2000型移频信号检测技术研究与实现
2014-03-26刘小春刘三帅
刘小春,张 蕾,刘三帅
(1.湖南铁道职业技术学院铁道供电与电气学院,湖南株洲 412001;2.株洲南车时代电气股份有限公司,湖南株洲 412001)
0 引言
ZPW2000移频轨道电路[1]是移频自动闭塞系统的重要设备之一,定期测量移频轨道电路信号参数,不但是考核线路质量是否达标的必要手段,而且也是保证行车信号准确可靠,确保列车安全运行的重要条件。随着铁路技术的发展和行车密度的增加,铁路系统对移频轨道电路信号检测的要求越来越高。铁路电务部门对移频轨道电路信号的检测,希望有较高的频率分辨率。因此,急需研究新的移频轨道电路信号检测算法与仪器。
移频信号的检测方法包括时域法与频域法。时域法抗干扰能力差,无法准确检测;频域法抗干扰能力强,但采样点多时运算量较大,实时性差。文中在频域检测算法基础上,采用欠采样技术和离散频谱校正算法实现了对ZPW2000型移频信号的高精度实时检测,有一定的参考实用价值。
1 移频信号
ZPW2000型移频轨道电路信号采用相位连续的移频键控(FSK)信号,具体参数为:频偏为±11 Hz,中心频率1 700 Hz、2 000 Hz、2 300 Hz和2 600 Hz 4个,低频从10.3 Hz按1.1 Hz等差级数递增至29 Hz,共18个。
由文献[2]可知, 其时域表达式为:
S(t)=A0cosθ(t)=A0cos[ω0(t)+g(t)]
(1)
式中:A0为移频信号的幅度;ω0为载频角频率。
式中Δω为移频信号的角频偏。
移频轨道电路信号检测就是要检测出载频频率f0,低频调制频率信息f1=1/T,频偏频率Δf=Δω/2π.由于S(t)是周期信号,则将式(1)用傅里叶级数展开,导出移频信号的频谱表达式[2]:
式中:Ω0为基频;m为移频指数,m=Δω/ω1=Δf/f1;n为边频数,n=…-2,-1,0,1,2…。
移频信号的离散频谱图如图1所示。
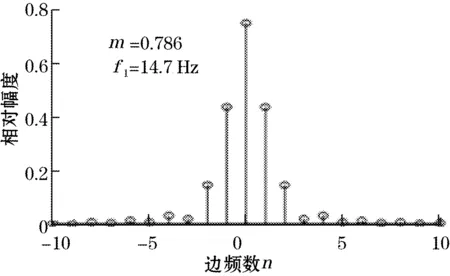
图1 ZPW2000移频信号频谱图
ZPW2000型移频信号的频谱特征为单峰谱,通过分析其频谱特性可得到以下参数:
(1) 载频频率f0:频谱图中幅值最大处的频率;
(2) 低频调制频率f1:两条相邻边频对应频率之差的绝对值;
(3) 频偏Δf:通过Δf=f1·m来计算。
2 移频信号频域检测算法
在频域检测方法[3]中,常见的检测方法是离散傅里叶变换(DFT),它具有较强的抗干扰能力,而快速傅里叶变换(FFT)是DFT的快速算法。在频谱分析中,对信号进行DFT计算,通常采用窗函数来截断信号使其变成有限时长的信号。由DFT得到的频谱是一系列的离散谱线。如果周期信号的频率正好对准某一谱线时,则得到的频率是准确的。但在通常情况下,信号频率没有对准峰顶而在2条谱线之间,则峰值谱所对应的频率就不准确。因此,要得到准确的频率,需要频谱的校正[4]。
离散频谱分析的误差产生原因主要来自两个方面:由于非整周期采样信号产生的频谱泄露;时域加窗截断信号使频域离散化的结果。
2.1 汉宁窗校正原理
在频谱分析中,汉宁窗定义为:
其频谱主瓣函数为:
主瓣函数图形如图2所示。

图2 汉宁窗频谱主瓣函数
主瓣包含4条谱线,且函数满足以下条件:
(x-1)f(x)+(x+2)f(x+1)=0
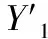
汉宁窗频域幅值谱抽样的结果如图3所示,用谱线序号来表示横坐标,所对应的频率为:
式中:fs为采样频率;N为分析点数。

图3 汉宁窗频域幅值谱抽样
设幅值谱峰谱主瓣内的2条谱线K,K+1对应的幅值分别为YK,YK+1则平移后的重心坐标x0满足:
(K-x0-1)YK+(K-x0+2)YK+1=0
计算得
同理,用K-1,K条谱线求重心时有:
令x0=K+ΔK,得到频率校正公式:
校正频率公式为:
2.2 采样频率的确定
ZPW2000型移频信号最高频率可达2 611 Hz,由Nyquist采样定理可知,采样频率应不小于5 222 Hz.但处理器进行FFT运算时的采样点数太多会使计算时间加长,若采样点数过少会使频率分辨率(Δf=fs/N)下降,进而导致检测精度降低。为了既能提高检测精度,又能降低采样点数,故对ZPW2000型移频信号采用欠采样技术[5]。
欠采样就是指以低于Nyquist采样频率K倍的采样频率进行无失真采样。从频域上分析可知,信号的采样过程其实就是原信号频谱沿频率轴的搬移过程,选择采样频率的核心问题就是使搬移后的频谱不和原频谱的频率部分混叠。所以采样频率fs应满足如下关系:
即:
式中:k=1,2……b,b=[fH/B] 向下取整;fH与fL为信号的上、下截止频率。
这样就可保证原信号频谱中的上下截止频率都不与上下边带重叠,即采样信号的频谱无混叠现象。
根据移频信号频谱特征及欠采样知识,可归纳出欠采样前后中心频率的关系[3]:
式中:fs为采样频率;f0为欠采样后的中心频率。
应用欠采样技术,当载频为1 700 Hz、2 300 Hz和2 600 Hz时采样频率fs选为2 048 Hz,载频为2 000 Hz时采样频率fs选为2 560 Hz.
3 设计实现
TMS320VC5509A[6]基于TMS320C55xDSP核的16位定点DSP,主频最高达200 MHz,超低功耗,具有超强的数据运算处理能力;可通过高速的多通道缓冲串口McBSP与其他DSP、AIC等器件相连;外设中集成了USB、ADC、IIC等模块。VC5509A的这些特点,使其非常适合于构成一个全功能的便携式DSP应用系统。
3.1 硬件平台设计
根据应用系统功耗、数据处理能力、便携性等因素,设计了基于TMS320VC5509A的移频信号测试硬件电路,其原理框图如图4所示。

图4 移频信号检测硬件原理图
其中A/D采用TLC320AC01[7],其可以与TMS320VC5509A无缝连接。TLC320AC01是一个14位、音频(大约12 kHz带宽)、内含开关电容式带通抗混叠输入滤波器和低通重构输出滤波器的模拟接口电路(AIC),最高采样频率为43.2 kHz.其内部电路的配置和性能参数的设定,比如采样频率、滤波器带宽和增益高调整等,都可以通过对它内部的8个数据寄存器写入控制信息来实现。输出数据是以2的补码格式进行传输。DSP与TLC320AC01的连接方式如图5所示。

图5 DSP与TLC320AC01的连接方式
3.2 检测算法设计
移频信号检测算法采用欠采样技术和复数傅里叶变换,首先对采样的数据进行连续的复数存储,然后采用时间抽取基2-FFT算法和离散频谱比值校正技术来对移频信号解调处理。其检测算法流程如图6所示。

图6 移频信号检测算法流程图
4 测试结果
为了对设计的移频信号参数检测算法进行验证,利用HP33120A信号发生器产生ZPW2000型的移频信号进行测试,将实测结果与设置参数进行对比,看误差是否满足要求。图7是载频1 700 Hz,低频10.3 Hz的移频信号测试结果。

图7 载频1 700 Hz移频信号测试结果
在11 Hz频偏下,分别在18种不同低频频率条件下,实测移频信号载频与实际值的误差统计图如图8所示。

图8 ZPW2000型移频信号载频实测误差图
由图8可以看出,ZPW2000型移频信号载频的检测误差最大值为0.2 Hz.
对每一种载频,分别在18种不同低频频率条件下,实测移频信号频偏与实际值的误差统计图如图9所示。

图9 ZPW2000型移频信号频偏实测误差图
由图9可以看出,ZPW2000型移频信号频偏的检测误差最大值为-0.02 Hz.
在11 Hz频偏下,分别在4种不同载频频率条件下,实测移频信号低频与实际值的误差统计图如图10所示。

图10 ZPW2000型移频信号低频实测误差图
由图10可以看出,ZPW2000型移频信号低频调制频率的检测误差最大值为-0.005 Hz.
通过试验表明,移频信号实测载频的误差绝对值在 0.3 Hz 以下,实测频偏的误差绝对值在 0.2 Hz 以下,实测低频调制频率的误差绝对值在 0.01 Hz 以下,实现了移频信号的准确检测;测得每次对移频信号的检测时间约为1.7 s,其中采样时间约为1 s,FFT运算运行时间约为0.5 s,解调校正算法运行时间约为0.2 s,满足实时性要求。
5 结束语
文中对ZPW2000移频信号频谱特征进行分析,采用欠采样技术和FFT频谱校正技术实现移频信号的准确检测,以低功耗高速数字信号处理器TMS320VC5509A为核心,进行了移频信号轨道电路测试平台硬件设计,利用DSP作为数字信号处理器的优点,使仪器结构设计简洁、性能可靠,具有一定的应用参考价值。
参考文献:
[1] 林瑜筠.铁路信号基础.北京:中国铁道出版社,2006.
[2] 费锡康.无绝缘轨道电路原理与分析.北京:中国铁道出版社,1993.
[3] 焦美鹏.轨道电路移频信号参数在线测试仪的研制:[学位论文].西安:西北工业大学,2012.
[4] 谢明,丁康.离散频谱分析的一种新校正方法.重庆大学学报,1995,18(2):48-54.
[5] 李惠光.欠采样频率的选取.传感技术学报,1998,11(4):15-22.
[6] 杨明极,刘喜庆,张洪洋.轨道移频信号频率参数检测方法的研究.仪表技术与传感器,2012(7):87-89.
[7] TI公司.TMS320VC5509A Fixed-Point Digital Signal Processor Data Manual,2005.
[8] TI公司.TLC320AC01I Data Manual,1997.
