联合频偏估计与循环矩的MPSK信号调制识别算法

吴 涛，狄旻珉，黄国策

(空军工程大学信息与导航学院，陕西西安 710077)

0 引言

调制识别指通过对接收信号的统计特征分析以判别信号的调制样式，调制识别具有很高的应用价值。调制识别算法主要分为基于决策理论的最大似然假设检验方法和基于模式识别的方法[1-2]。前者对模型失配很敏感且计算复杂度高，而后者运算简单。基于模式识别的方法包含特征提取和分类两部分，其中特征提取有基于瞬时信号参数[3]、基于傅里叶变换[4]、基于小波变换[5]、基于高阶统计量和循环统计量[6-7]等多种特征。模式识别的分类器也应用到调制识别，如人工神经网络[8]、支持向量机[5]和决策树[9]等。在目前关于多进制相移键控(MPSK)信号的调制识别算法中分类QPSK和8PSK信号的文献较少，而且很少考虑频偏的影响。

文中利用广泛应用于调制识别的循环统计量提出针对MPSK信号的调制识别算法，该算法主要解决了频偏对算法性能的影响。

1 信号模型

单载波调制一般通过基带信号改变载波的幅度、频率和相位来实现。在高斯白噪声(AWGN)信道下接收信号的复数域基带信号可以表示为：

(1)

式中：α为接收信号幅度；T为符号周期；ε为时延偏差；Δfc为载频偏差；θ为相位偏差；s(i)为信号星座；p(t)为脉冲成形函数；ω(t)为高斯白噪声，且ω(t)与s(i)统计独立。

当s(i)表示MPSK信号时，其复域表达式为s(i)=ejθi，i=1，2，…M.其中θi在[0，2π]之间等间距分布。

2 循环统计特征

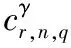
(2)

γ=k/T+(n-2q)Δfc

(3)

式中：k为整数；β=k/T；cs，n，q是信号星座的累积量；(*)u代表取共轭运算。

循环累积量和循环矩的转换关系表示如下：

(4)

式中：n表示阶数；Ip={1，…，p}；集合I表示满足∪Ip=I条件的无交连非空集合Ip的无序组合；q表示Ip中元素个数；αp和np分别表示Ip中第p项的循环频率和阶数；循环频率β和α的关系为β=α1+…+αq.

由式(2)、式(3)知，当k=0且q=n/2时，接收信号的循环累积量与载频偏差Δfc、相位偏差θ无关。当k=0且q≠n/2时，接收信号的循环累积量与载频偏差Δfc有关。当n≥3，由于高斯随机变量的高于三阶的循环累积量为零，因此对式(2)取模可以得到循环累积量与时延偏差ε也无关。

表1是MPSK信号星座的累积量。当q=n/2时，可以看到cs，2，1不能区分BPSK、QPSK和8PSK信号；cs，4，2和cs，6，3只能区分BPSK和QPSK/8PSK，不能区分QPSK和8PSK；cs，8，4可以区分BPSK和QPSK/8PSK信号。由于cs，8，4易受噪声的干扰且-33和-34很接近，因此cs，8，4对QPSK和8PSK信号的分类能力受限。当q≠n/2时，可以看到，虽然cs，2，0受载频偏差和时延偏差的影响，但BPSK的cs，2，0=1，QPSK和8PSK的cs，2，0=0，该特征对于两类信号的区分十分明显。QPSK的cs，4，0=1，8PSK的cs，4，0=0，cs，4，0对于QPSK和8PSK的区分也十分明显，且该特征不受时延偏差的影响。另外，cs，6，0和cs，8，0也具有分类信号的能力，但其比cs，2，0和更易受噪声的影响。由式(4)知

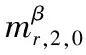
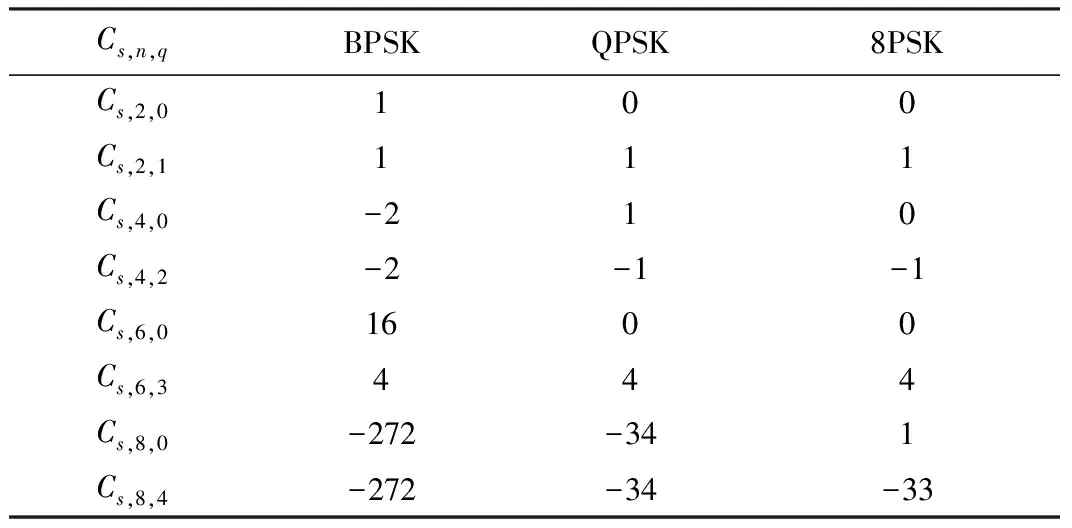
表1 MPSK的累积量

3 频偏估计算法

图1 BPSK信号的与γ的关系

(5)

式中Ω表示待定频率集合，该集合通过对载频估计误差区间离散化得到。

随机频偏估计(Random Frequency Offset Estimation，RFOE)算法是针对式(7)作出的简化，其步骤如下：

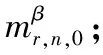
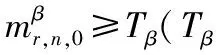
步骤3：若N>TN(N和TN分别是已搜索数和其最大值)，检测失败，否则从Ω中去除频率β后转步骤1；

步骤4：在当前频率β邻域Ωβ内利用式(7)得到频偏估计，其中Ωβ所含频率较少。

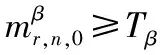
(6)

式中NΩ表示Ω中频率数。

ΤΝ的估计值可以表示为：

(7)

式中δ为允许的漏检概率。

第i次查找成功的概率为：

(8)

则平均查找次数为：

(9)

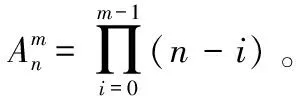
检测率表示为平均检测次数与频率数NΩ的比值：

(10)

可以验证，当NΩ或频率数k较大时，η与ΝΩ无关。图2是检测率η和频率数k的关系曲线图。从图2可见，当k≥5时检测率逐渐趋于平缓，而当k<5时，检测率η随着k的减小显著增大。

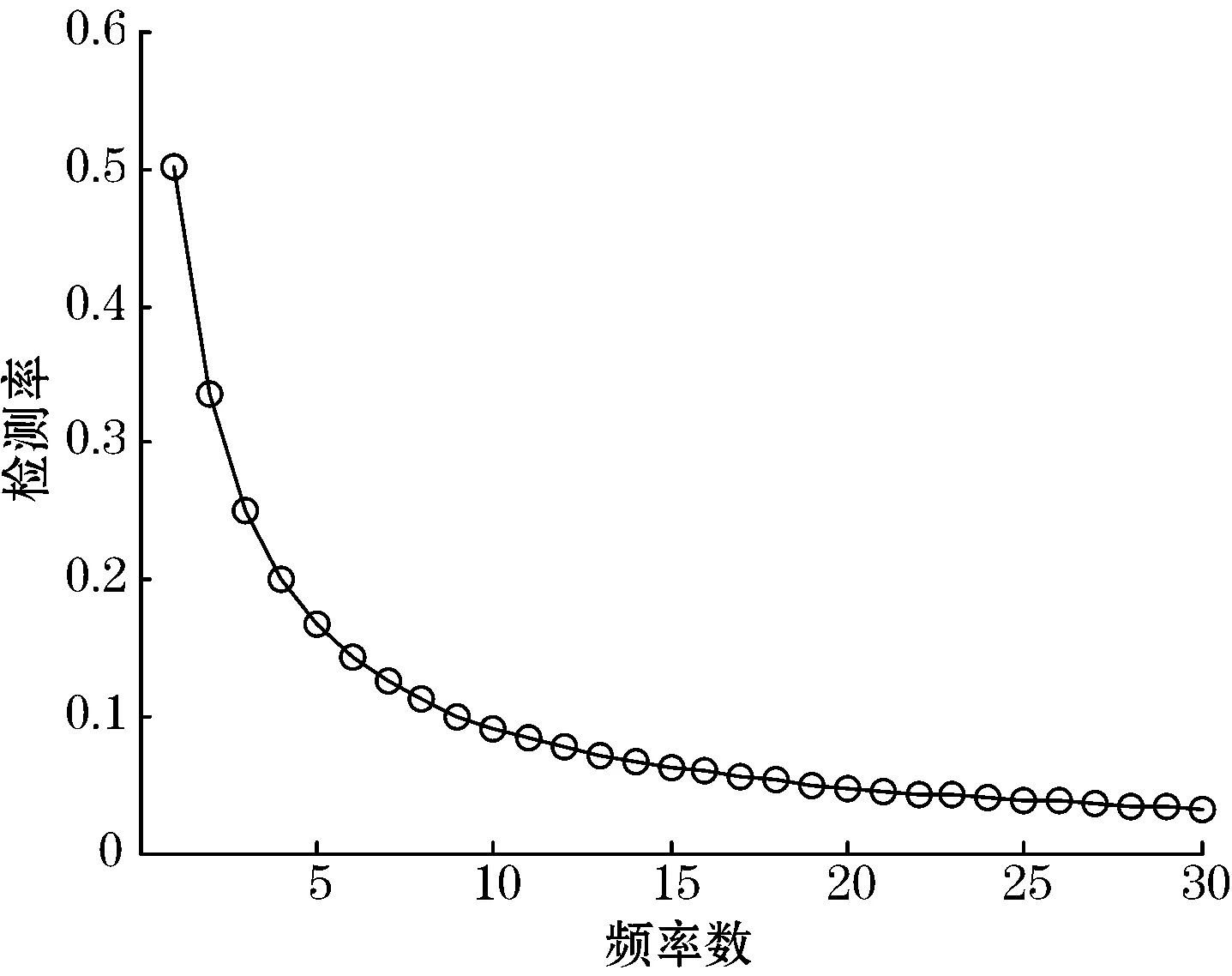
图2 检测率η与频率数k的关系

4 联合频偏估计与调制识别算法

利用RFOE算法也可以直接分类2种信号，将RFOE算法步骤3和步骤4修改为：

步骤3：若N>TN，输出信号2，否则从Ω中去除频率β后转步骤1；

步骤4：输出信号1。

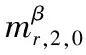
步骤1：使用RFOE-2检测信号，若输出为信号1，则信号为BPSK，算法结束，否则转步骤2；

步骤2：使用RFOE-4检测信号，若输出为信号1，则信号为QPSK，否则为8PSK，算法结束。

5 仿真结果与分析

仿真实验分别对Φ1={BPSK，QPSK/8PSK}和Φ2={QPSK，8PSK}两类信号，主要原因为：很多文献只考虑BPSK和QPSK，或者不考虑频偏；文中算法对BPSK和QPSK/8PSK信号的分类能力远高于其对QPSK和8PSK信号的分类能力。参考算法以文献[11]算法为例。除特别指出外，仿真参数分别为：采样率为符号率的8倍；脉冲成形滤波器为根升余弦成形滤波器(滚降系数为0．35)；时延偏差ε取[0，1]之间的随机值；相位偏差θ取[0，2π]之间的随机值；采样数据中符号数N=1 000。

5.1 实验1：载频偏差与识别率

图3是文中算法和文献算法平均识别率与归一化载波频偏ΔfcT的关系曲线图。其中SNR=-1 dB.可以看出，文中算法分类BPSK和QPSK时平均识别率始终保持100%，不随ΔfcT的变化而变化；文献算法的平均识别率在ΔfcT=10-3时急剧下降，在ΔfcT<5×10-4时保持稳定。在分类QPSK和8PSK信号时，文中算法随着ΔfcT的变化而略有起伏，但总体保持恒定，对ΔfcT体现了较好的鲁棒性，而文献算法平均识别率在ΔfcT>10-4时急剧下降，对ΔfcT比较敏感。

图3 平均识别率与ΔfcT的关系

5.2 实验2：SNR与识别率

图4是文中算法和文献算法对{BPSK，QPSK/8PSK}信号的平均识别率与SNR的关系曲线图。其中，载频偏差Δfc=0，文献算法N=1 000和N=100 000，文中算法N=1 000。可以看到文中算法在SNR=-11 dB时对BPSK和QPSK的平均识别率达到100%；而文献算法在SNR=-2 dB时才达到100%。文中算法性能比文献算法高出9 dB.另外，当符号数为100 000时，文献算法在SNR=-8 dB时平均识别率达到100%，但这一结果仍低于文中算法符号数取1 000时所达到的结果。这种现象的主要原因是四阶循环统计量比二阶循环统计量对噪声更敏感。

图4 BPSK和QPSK/8PSK信号的平均识别率与SNR的关系

图5是文中算法和文献算法对{QPSK，8PSK}信号的平均识别率与SNR的关系曲线图。其中，载频偏差分别取ΔfcT=10-5和ΔfcT=10-4。可以看出，在ΔfcT=10-5和ΔfcT=10-4两种情况下，文中算法的平均识别率均高于文献算法。当载频偏差较小时，两种算法的平均识别率接近，但当载频偏差较大时，文献算法平均识别率急剧下降。

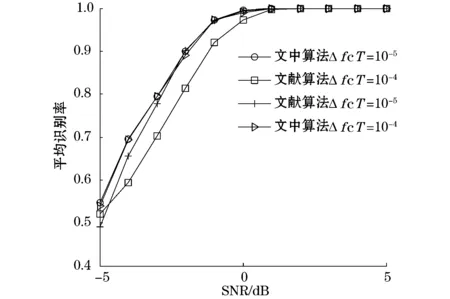
图5 QPSK和8PSK信号的平均识别率与SNR的关系

6 结论

文中研究了BPSK、QPSK和8PSK信号存在载波频偏时的调制识别问题，提出了一种联合频偏估计与循环矩的调制识别算法。理论分析和仿真结果表明文中算法对载波频偏具有较强鲁棒性的同时，实现了低SNR条件下BPSK和QPSK/8PSK信号的分类。

参考文献：

[1] XU J L，SU W，ZHOU M． Likelihood-ratio approaches to automatic modulation classification．IEEE Trans．，2011，41(4)：455-469．

[2] DOBRE O A，ABDI A，BAR-NESS Y，et al．Survey of automatic modulation classification techniques：classical approaches and new trends．Commun．，IET，2007，1(2)：137-156．

[3] POPOOLA J J，VAN OLST R．A novel modulation-sensing method．Vehicular Technology Magazine，IEEE，2011，6(3)：60-69．

[4] GUAN H B，YE C Z，LI X Y．Modulation classification based on spectrogram．Machine Learning and Cybernetics．Proceedings of 2004 International Conference on IEEE，2004，6：3551-3556．

[5] PARK C S，CHOI J H，NAH S P，et al．Automatic modulation recognition of digital signals using wavelet features and SVM．Advanced Communication Technology．10th International Conference on IEEE，2008，1：387-390．

[6] GANG H，Jiandong L，Donghua L．Study of modulation recognition based on HOCs and SVM．Vehicular Technology Conference．IEEE 59th，2004，2：898-902．

[7] DOBRE O A，ONER M,RAJAN S,et al．Cyclostationarity based robust algorithms for QAM signal identification.IEEE Commun，2012：12-15．

[8] XU Y，GE L，WANG B．Digital modulation recognition method based on self-organizing map neural networks．WiCOM’08．4th International Conference on IEEE，2008：1-4．

[9] YUAN J，Zhao-Yang Z，Pei-Liang Q．Modulation classification of communication signals．Military Communications Conference．IEEE，2004，3：1470-1476．

[10] DOBRE O A，ABDI A，BAR-NESS Y，et al．Cyclostationarity-based modulation classification of linear digital modulations in flat fading channels.Kluwer Wireless Personal Commun．，2010，54：699-720．

[11] 陈卫东，杨绍全．基于循环累量不变量的MPSK信号调制识别算法．电子与信息学报，2003，25(3)：320-325．