基于高阶统计量滤波器的离子浓度信号测量

周安然，杨光永，2，吴海锋，赵锦剑，朱 芹

(1．云南民族大学电气信息工程学院，云南昆明 650500；2．华南理工大学机械与汽车工程学院，广东广州 510640)

0 引言

近20年来，离子浓度测量的研究热点主要是围绕电极过程动力学[1]、提高离子电极性能[2]和离子浓度信号通道特性[3]等方面进行，主要分为两大类：一类着眼于改进离子浓度仪的硬件设计、电气特性[4]，构建测量平台的最优系统方案，如选择性、免校准离子电极[5]，采用具有超高输入阻抗、高共模抑制比和极低输入偏置电流的仪表放大器[6]，采用可配置模拟前端(AFE)专用器件(如LMP91200)，选择16位甚至24位Δ-Σ型AD转换器以提高信号的转换精度，或采用带AD转换器的增强型混合单片机[7]；另一类侧重于噪声抑制和非线性标定技术，采用现代信号方法，包括递归最小均方误差滤波器(RLS)[8]、最大熵谱方法[9]、盲源分离[10]等，抑制超高斯和亚高斯噪声，以低阶统计量信号的稳态过程看待离子活度测量系统。

无论是在线水质监测，还是离线水质样品分析，由于选择性离子电极的暂态响应特性，使离子活度信号不可避免地混入高斯噪声和非高斯噪声[11]，而基于低阶统计量的RLS、LMS滤波器很难抑制或消除高阶统计噪声的影响，从而降低离子浓度仪的测量精度和信噪比。

为了提高离子浓度仪的测量性能，文中利用高阶统计量均方误差准则对非高斯噪声的强一致估计特性，在测量系统的模拟前端与微处理器单元之间加入高阶统计量自适应滤波器(HoSRLS)，消除离子浓度信号中的超高斯和亚高斯噪声。

1 高阶统计量自适应滤波器

设离子浓度测量系统的输出过程为：

(1)

式中：误差e(n-k)是均值为零、与冲激响应h(n)相互独立、同分布的随机信号。

x(n)经过滤波器的输出εx，θ(n) 为：

(2)

在四阶统计量的均方误差代价函数：

(3)

式中：

B=E[y(n+k1)εy，w(n)]E[y(n+k2)εy，θ(n)]；

(4)

(5)

式中：γ2c和γ4e分别是e(n)的二阶和四阶累积量；β为标量因子。

(6)

按高阶统计量均方误差准则建立新的强一致估计器：

Φw=φ

(7)

满足递归形式：

(8)

窗口宽度为2M+1，每次有2M+1个数据被分析。式(7)中w是滤波器在n时刻的抽头权向量：

w(n)=[w0(n)，w1(n)，…，wM-1(n)]T

(9)

使y(n)-y(n+1)达到最大值：

max[y(n)-y(n+1)]

(10)

即式(10)成立时所取得的n即为AR(p)的阶数。

2 仿真和模型验证

为了验证高阶统计量自适应滤波器的收敛速度和噪声抑制性能，文中以不同噪声功率的加性噪声、不同幅值的窗函数设计仿真数学模型，以获得仿真数据。

加性噪声由三类噪声组成：

(1)高斯白噪声。X：N(μ，σ2)，其中，均值μ=0，方差σ2=0.1，噪声功率Ρ=5 dBW，用于模拟正态分布的加性噪声分量；

(2)瑞利分布噪声。X：Reyleigh(B)，分布参数B取值25，用于模拟亚高斯噪声分量；

(3)指数分布噪声。X：Exponential(λ)，率参数λ=0．1，模拟超高斯噪声分量。

设采样序列为k∈[1，200]，以氢离子电极动力特性为仿真对象，将参考信号d划分为不同幅值的Blackman-Harris窗函数d1、d2和d3：

系统仿真数学模型为：

x=d+N(P)+Reyleigh(В)+Exponential(λ)

在采样序列k1=160、k2=100、k3=40，分别获得3个极值点，以测试在极值和不同峭度条件下HOSRLS滤波器的收敛性能。

HOSRLS和RLS滤波器的仿真结果如图1所示，从图中可看出，当迭代次数较少(i=5)，在峭度和偏度较大的区域(如A、B和C)，RLS滤波器仍然含有超高斯和亚高斯噪声分量Reyleigh(B)和Exponential(λ)，且超调量高于10%，而HOSRLS则完全滤除超高斯和亚高斯噪声，其收敛速度优于RLS.

图1 HOSRLS和RLS滤波器的仿真结果

另一方面，在同样的迭代次数(i=5)条件下(如图2所示的D、E和F点)，RLS和HOSRLS抑制高斯白噪声的能力相当，但对于叠加非高斯噪声分量的系统仿真数学模型来说，HOSRLS滤波器在采样序列k1=160、k2=100、k3=40分别获得45 dB、28 dB和55 dB，而RLS分别获得25 dB、25 dB和22 dB，可看出HOSRLS比RLS滤波器获得较高的信噪比。

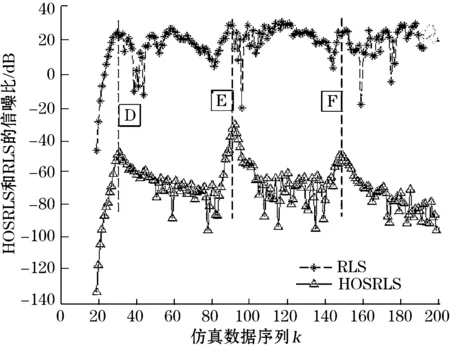
图2 HOSRLS和RLS滤波器的信噪比比较

3 实验及结果分析

实验平台的总体结构框图如图3所示，在Cyclone III系列EP3C10F256上创建系统，以标准型NIOS II微处理器为核心，将HOSRLS滤波器模块挂接到Avalon总线上，以硬件加速方式设计HOSRLS模块，NIOS II微处理器访问HOSRLS模块，并实时计算离子浓度，经IEEE 802．15．4收发片上系统CC2430，将离子浓度值发送到远程数据管理中心。

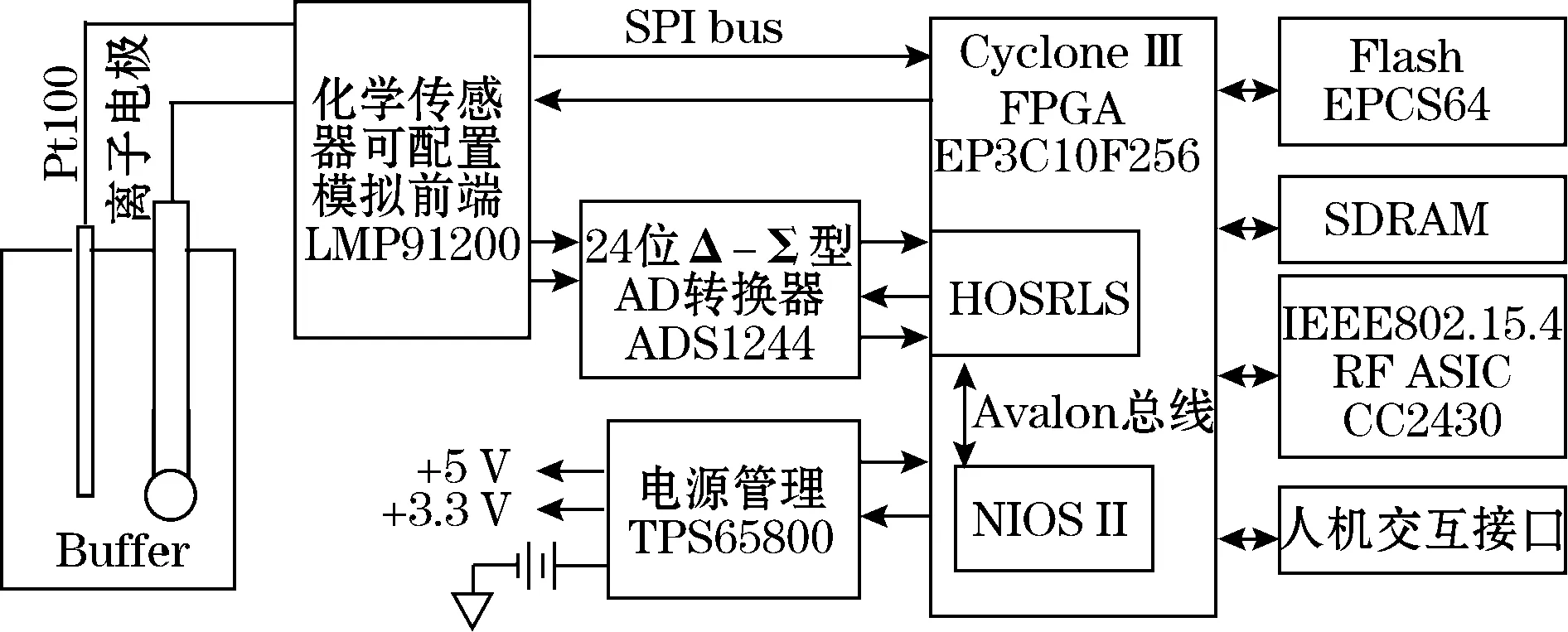
图3 无线传感器网络离子浓度监测节点结构框图

为了提高信号整定单元的性能，减少温度漂移，取消高输入阻抗运算放大器ICL7621和电压温度漂移补偿电路，精简传感器及其模拟前端的电路结构，采用化学传感器可配置模拟前端LMP91200，NIOS II处理器经SPI总线，配置离子电极的共模电压、对温度补偿传感器的电流源编程配置、选择标定/测试模式等。

无线传感器网络离子浓度监测节点在1．68、4．01、6．86、7．00和10．00等不同pH标准缓冲溶液、25 ℃标定实验条件下，测量并计算其绝对误差和独立线性度，其结果见表1。可看出，加入HOSRLS滤波器模块之后，离子浓度监测节点的线性度有明显提高。

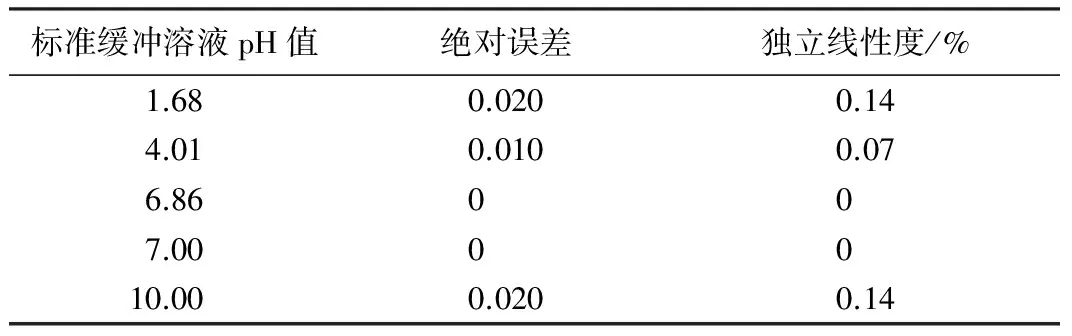
表1 绝对误差和线性度测试结果

4 结论

在文中采用基于四阶累积量的均方误差准则来设计自适应滤波器，用于离子敏传感器来测量溶液中氢离子浓度。仿真和实验结果表明高阶统计量自适应滤波器方法比低阶自适应滤波器方法在氢离子浓度的测量上，极大地提高了信噪比，滤波效果明显优于低阶自适应滤波器，收敛速度更快，这也验证了高阶统计量能有效地抑制高斯噪声和非高斯噪声。

参考文献：

[1] 查全性．电极过程动力学导论．3版 北京：科学出版社，2002．

[2] 李芬．锌空气电池之气体扩散电极性能研究：[学位论文].合肥：中国科学技术大学，2010．

[3] 黄运生，毛先柏，陈学．基于微控制器的智能钴离子浓度分析仪．仪表技术与传感器，2005(10)：6-8．

[4] 杨光永．KA0324A 离子浓度计的研究与设计：[学位论文].昆明：昆明理工大学，2005．

[5] 马钰华．金属离子选择性电极的研究及应用：[学位论文].重庆：西南大学，2010．

[6] 黄勤，周婷，刘益良，等．高共模抑制比脑电放大电路设计．仪器仪表与检测技术，2009，28(4)：77-79．

[7] 卢立苹．离子浓度计的研制：[学位论文].沈阳：东北大学，2008．

[8] 江清潘，常太华，朱红路，等．自适应噪声消除算法的性能比较与仿真．科学技术与工程，2009，9(19)：5835- 5839．

[9] 聂士忠，王玉泰．最大熵谱分析方法和MATLAB中对短记录资料的谱分析．山东师范大学学报(自然科学版)，2005，20(3)：40-41．

[10] CARDOSO J F．Blind signal separation：statistical principles．Proceedings of the IEEE，1998，86(10)：2009-2025．

[11] YANG G Y,HU G Q,GUO B．Multiple Reflection Cancellation Using High Order Statistics Adaptive Filter for Scattered Triangulation Laser Displacement Sensor．Advanced Materials Research，2013，774-776：1613-1616．

[12] DELOPOULOS A N,GIANNAKIS G B．Strongly Consistent Identification Algorithms and Noise Insensitive MSE Criteria．IEEE Transactions on Signal Processing，1992，40(8)：1955-1970．

[13] 田昭武．电化学研究方法．北京：科学出版社，1984．