超声波热量表流量计算的新方法
2014-03-26吴叶兰黄亚楠陈红军
吴叶兰,赵 瑾,黄亚楠,陈红军
(1.北京工商大学计算机与信息工程学院,北京 100048;2.北京理工大学机械与车辆学院,北京 100081;3.北京淳堂科技有限公司,北京 100081)
0 引言
随着国家对热量收费制度的改革,热量表技术逐步得到了提高。目前,虽然热量表的类型有多种,超声波热量表却因其结构简单、抗干扰性强、精确度高、重复性好、安装维修方便等优势得到了广泛应用[1]。但是现有的超声波热量表在进行流量计算时,大都是采用传统的计算方法,测量精度易受管壁情况、液体温度、流动状态等诸多因素的影响[2],而且计算较为复杂,测量精度很难达到国家规定的要求。
为了研制一种高精度的超声波热量表,在分析影响流量测量精度因素的基础上,着重分析了流量计算方法所带来的误差,研究了一种新的流量计算方法——流量分段插值法。该方法利用线性回归算法和分段插值算法建立了流量与时间差之间的关系曲线,并制定了温度转换表格,将不同温度下的时间差转换成特定温度下的时间差,便于对时间差的统一处理,避免了温度变化对超声波传播速度带来的影响,提高了流量计算的精度和可靠性,促进了热量表中流量测量技术的发展。
1 时差法流量测量原理
时差法超声波热量表的工作原理图如图1所示[3]。为了测出超声波在顺、逆方向的时间差,在直径为D的热量表管段两侧安装两个超声波换能器即换能器A和换能器B,两换能器与管道轴线之间的夹角为θ,流体流速为v,超声波在静水中传播速度为c,传播路径为L。

图1 时差法热量表工作原理图
当换能器A用于发射,换能器B用于接收时,超声波在顺流方向的传播时间为:
(1)
当换能器B用于发射,换能器A用于接收时,超声波在逆流方向的传播时间为:
(2)
时间差Δt似为:
(3)
由此可得时差法的流速公式为:
(4)
由(4)式可见,只要求出Δt的值,就可以得到流速,进而得到流量。
2 流量的计算方法
2.1 传统的流量计算方法
对于圆管流体的测量,其瞬时流量公式为:
(5)
在时间t1,t2内流经管段的总流量Q为:
(6)
由于式(6)中的积分运算在单片机内是不容易实现的,实际应用中通常会把测量区间[t1,t2] 分为N个间隔为t的时间段,进而将连续的积分运算近似为单片机容易实现的离散求和运算。处理后,流量的计算公式可变为:
(7)
但是这种计算方法存在以下2个缺点:
(1)利用式(5)计算流经管段截面的流量时用的是面平均速度vm,而由式(4)只能得到线平均速度。这样,就需要利用雷诺系数将测得的线平均速度修正为面速度[4-5],而雷诺系数会随流体的流动状态不同而不同,所以在实际计算中面速度vm的求法较为复杂,而且难以保证精度。
(2)超声波在水中的传播速度会随流体温度的升高而变大,相应的时间差也会因温度的变化而变化[6]。若将式(4)中的c用固定常数代入,则会带来测量误差,影响测量精度。
为避免上述两个因素对流量测量的影响,研究了流量分段插值法来计算在某一流量点qi下,时间段t(单位为s)内流过管段的流量。由式(7)知,只要qi计算准确,就能保证总流量Q的计算也是准确的。
2.2 流量分段插值法
由时差法流量测量的原理可知,流量是根据超声波传播时间差来求的,可以理解为在不同流量点下所测得的时间差也是不同的,即qi与Δt之间存在着某种函数关系。在这个函数关系中将时间差Δt看作自变量,流量qi看作因变量。
测试数据表明,在热量表的整个测量范围内,qi随Δt的变化不是线性的,因此需要对整个量程内的流量(单位为L/h)分段进行处理[7-8]。首先要选择好分段点,并对这些流量点进行校准,使得热量表在每个区间端点处测得的流量是准确的,然后根据端点值确定整个流量区间内qi与Δt之间的函数关系,再利用这些端点流量进行插值计算,就可以求出某一区间任意流量点在时间段t内的流量。同理,也就可以求出整个量程内任意流量点在时间段t内的流量。
在户用热量表中,常用的是DN20管径,对于这种管径的热量表,国家规定的最小流量为50 L/h,最大流量是5 000 L/h.考虑温度变化对时间差的影响,通过对大量的实验数据进行分析,制作了适用于量程范围内任意流量点下的温度调整比例表格。利用该表格,可将不同温度下的时间差转换成某一特定温度(如50 ℃)下的时间差。这样计算时就只需考虑特定温度下,时间差与流量的对应关系。只要在该温度下流量值是准确的就可以保证在其他温度时测得的流量也是准确的,从而避免了温度变化带来的误差。
根据相应的的测试结果,选择2 500 L/h、750 L/h、50 L/h这3个流量点作为分段点,即将流量量程分段为[50,600],[600,2 500],[2 500,5 000] 这3个区间。测量时,将测得的时间差全部转换到50 ℃下,并根据转换后时间差的大小判断对应的流量点所在的区间[q1,q2] 。由于区间端点处对应t的时间段内的流量q1、q2已经过校准,即该段内qi与Δt的函数关系是已知的,就可以利用下面的插值公式(8)求出时间段t内流经管段的流量。
(8)
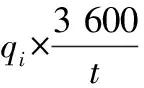
这样,根据流量的插值公式就可以计算出在50 L/h和5 000 L/h之间的所有流量点在t时间内的瞬时流量,然后利用式(7)将每个t时间内的流量qi累加就可以得到N×t时间内的总流量。
这种方法不再利用传统的式(5)、式(6)来计算流量,避免了由于流速分布不均和温度变化带来的误差,是一种新的计算方法。在实际应用中,只要标定的流量点和流量点的个数适当,就可以达到较高的测量精度。
3 误差分析
按照上面介绍的流量分段插值算法,研制了一种高精度超声波热量表,并对其流量的测量精度进行了测试。测试时,采用D20管段,在标准校验台上对热量表进行了测试。按照检定要求,超声波热量表的测量精度应在不同温度介质下分别进行检定,但由于高温下难以保证温度恒定,限于目前实验条件,只进行了常温(20 ℃左右)介质下的流量检定。检定采用超声波热量表样机与标准校验台上的流量计对照测量并分别读数的方法进行,流量的测试范围从33 L/h到5 000 L/h.测试结果如表1所示,误差曲线如图2所示。
从误差曲线可以看出,在整个量程范围内,流量的测量误差均小于2%,达到了国家的标准要求,同时在小流量点33 L/h时误差也不超过2%,完全能够满足国家不小于3%的要求,取得了显著的效果,测试结果证明该流量计算方法是合理可行的。
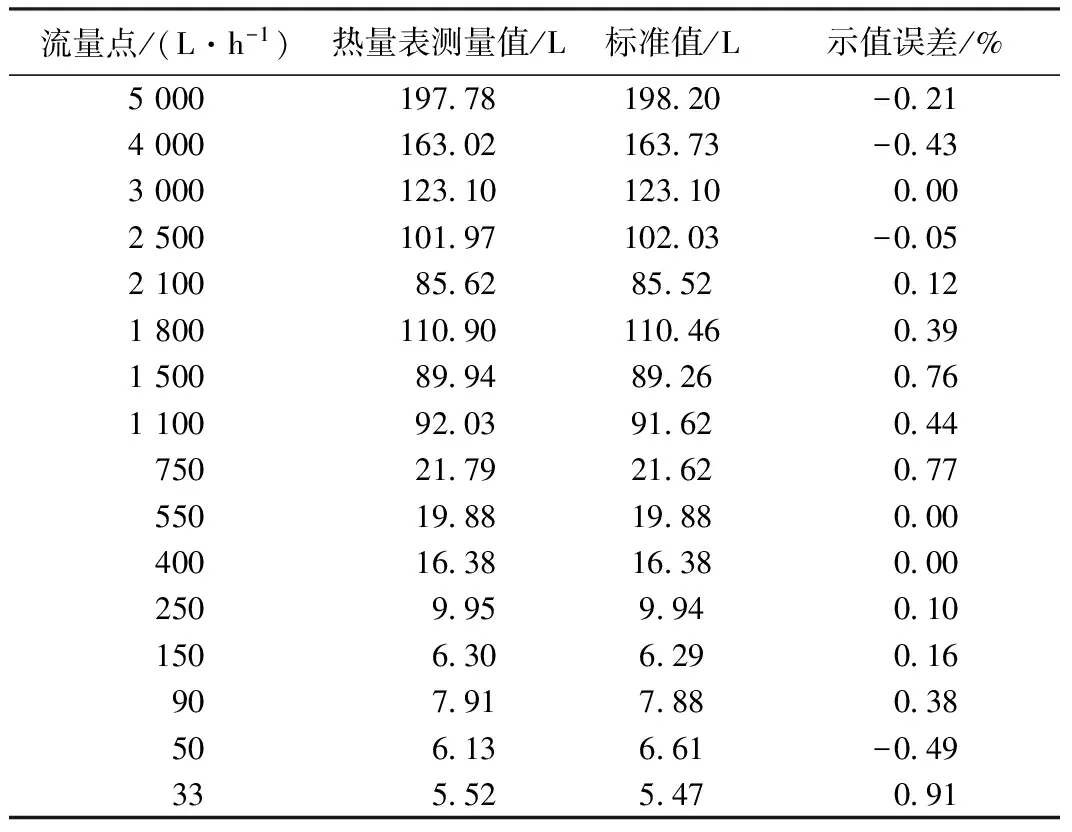
表1 测试数据

图2 误差曲线
4 结束语
超声波热量表是热量测量技术的发展方向。为了提高测量精度,分析了影响时差法超声波热量表中的流量计算精度的主要因素,研究了流量分段插值算法。在使用该方法时,只要准确地制定温度转换表、合理地设置流量分段点,就可以确保流量测量的高精度和稳定性,能够满足国家2级表的标准要求,具有一定的理论意义和实用价值。
参考文献:
[1] 梅彦平,张明君,王延平,等.TDC-GP21在超声波热量表中的应用.仪表技术与传感器,2012(2):37-39.
[2] 晁智强,盛锋,韩寿松.时差法超声波流量计误差分析与研究.液压与气动,2009(6):64-67.
[3] 姚滨滨,张宏建,唐晓宇,等.基于时差法和TDC-GP2的超声波流量测量方法.自动化与仪表,2011,36(8):17-20.
[4] 梁国伟,蔡武昌,盛健,等.流量测量技术及仪表.北京:机械工业出版社,2005.
[6] 李利品.基于DSP的高精度超声波流量控制系统.仪表技术与传感器,2009(3):132-133.
[7] 李庆扬,王能超,易大义.数值分析.5版.北京:清华大学出版社,2008.
[8] 文小玲,刘翠梅,易先军,余飞,卢圣文.铂电阻测温的非线性补偿算法分析.传感器与微系统,2009,28(8):33-36.
