梯形明渠临界水深直接计算公式研究

徐海嵩，把多铎，张国辉，袁 璞

(西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100)

梯形明渠是水利工程中一种常见的断面形式，主要用于农田灌排和城市供水等渠道的设计，较其他断面形式应用更为广泛[1]。梯形明渠临界水深是水力计算中的重要参数之一[1-6],通过临界水深和正常水深的计算设计渠道的断面尺寸，从而确定工程量，这将直接影响工程的经济效益。所谓临界水深是指相应于断面单位能量最小值的水深[7]，该参数无法直接求解，而需求解一元高次方程[4-6]。常见的求解方法有试算法、图解法、迭代法[8]和近似求解法[9]等，其中试算法和图解法费时费力，而且误差较大[5,10]。

近年来，一些水利专家致力于梯形明渠临界水深的研究，相继提出了几种直接计算临界水深的公式，如刘善综公式[11]，王正中等公式[3,12]等。这些计算公式，往往引入无量纲参数即单位水面宽度[13-16]，并根据迭代原理，选取合适的迭代方程和迭代初值，从而可方便、快捷地计算出梯形明渠的临界水深。但是，这些计算公式从简捷性、计算精度等方面均存在不足[5]。本研究在前人研究的基础上，对迭代公式和迭代初值进行细致地分析和推导，提出新的直接计算梯形明渠临界水深的公式，并对比前人的公式进行了精度和误差分析，以期为梯形明渠临界水深的计算提供更为精确的计算方法。

1 临界水深的计算公式及迭代式

在推求临界水深时，大都引入无量纲参数“单位水面宽度”[10]，即临界水深(h1)所对应的水面宽度与梯形渠道底宽的比值，用λ表示。其中，λ等于1时，过水断面为矩形断面；λ等于+∞时，过水断面为三角形断面[6]。故梯形断面单位水面宽度取值范围为1<λ<+∞，其值反映了梯形明渠断面过流时过水断面的相对形状[5]。

于是有下面的等式：

(1)

由上式可得：

(2)

式中：λ为单位水面宽度；Bk为临界水深时对应的水面宽度，m；b为梯形渠道底宽，m；m为梯形渠道的边坡系数，非等腰梯形断面时m=(m1+m2)/2，其中m1、m2为梯形断面两侧边坡系数[11]；hk为梯形渠道的临界水深，m。

而明渠均匀流临界水深的计算公式[7]为：

(3)

式中：α为动能修正系数，取1.0；Q为过流流量，m3/s；g为重力加速度，取9.81 m/s2；Ak为相应于临界水深时的过水断面面积，m2。

对于等腰梯形过水断面[5-6]，有

Ak=(b+mhk)hk，

(4)

Bk=b+2mhk。

(5)

将式(1)、(2)、(4)、(5)代入式(3)并整理得：

(6)

(7)

为了与式(7)的形式相似，式(6)变为：

(8)

将式(8)恒等变形并整理，得：

(9)

然后，根据迭代原理，式(9)变为：

(10)

式中：λn为第n次求得的单位水面宽度值，λn+1为第n+1次求得的单位水面宽度值。

2 迭代公式的收敛性证明

采用迭代法计算时无法直接求解方程，一般需要进行试算才能求出迭代方程的解。但使用迭代法是有条件的，必须使推求的迭代公式收敛，这样才能保证计算值逼近所要求解的真值。因此，需首先对式(9)或式(10)进行敛散性判别，而本研究则需要证明式(9)或式(10)在区间1<λ<+∞是收敛的，证明如下：

对于式(9)，设λ=φ(λ)，则

(11)

φ2(λ)=4kλ1/3+1。

(12)

根据迭代理论，如果方程x=φ(x)的1个根为a,则迭代公式xn+1=φ(xn)收敛于a的条件是：在a的某一邻域|x-a|<δ内，使|φ′(x)|<1，那么该值域内任一点为初值的迭代都收敛于a，因此只要证明上式中的迭代函数φ(λ)的一阶导数的绝对值小于1，就可以证明该迭代函数是收敛的[5]。

因此，对式(11)两边求导，得：

(13)

将式(11)、(12)代入式(13)中得：

(14)

继续对φ′(λ)求二阶导数，可得：

由二阶导数可知，当λ∈(1,+∞)时，φ″(λ)∈(0,0.33)，即二阶导数大于零，迭代函数在其定义域内单调。当λ=1时，φ′(λ)=0；当λ=+∞时，φ′(λ)=0.17。因此，根据夹逼定理，当λ∈(1,+∞)时，φ′(λ)∈(0,0.17)，故|φ′(λ)|<1。

综上所述，对于任意的λ∈(1,+∞)，迭代公式(9)是收敛的。同理，可以证明式(10)也是收敛的。

3 迭代初值的合理选取和临界水深的直接计算

对于迭代计算，其收敛速度不仅与迭代公式有关，而且与迭代初值的选取也有关[5]，且迭代初值的选取更为重要，选取合理的迭代初值会加速迭代计算的收敛速度。对式(8)作恒等变形，即可得出迭代初值。

由式(8)得：

(15)

由于λ∈(1,+∞)，当λ趋近于正的无穷大时，λ=(4k)0.6，并以此作为迭代函数的初值，即λ0=(4k)0.6。将λ0代入式(9)，可得

(16)

将式(16)代入式(9)并整理，得：

(17)

为提高计算精度，可将式(17)代入式(9)并整理，得：

(18)

将式(17)或式(18)代入式(2),得：

(19)

或hk=

(20)

通过式(19)或式(20)可直接计算梯形明渠的临界水深，其中式(20)较式(19)计算的结果更加精确，然而在一般的工程实际中，式(19)的计算精度已经可以满足工程实际的要求。

4 临界水深直接计算公式的精度分析

4.1 几种常见的临界水深直接计算公式描述

国内外计算梯形明渠临界水深的方法和公式很多，但从准确性和间接性等方面考虑，有4套公式相对较好，分别如下所示。

①王正中等[3,12]公式：

(21)

②廖云凤[16]公式：

y=kl(1+kl)-0.372。

(22)

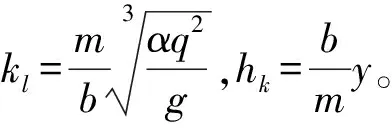
③刘善综[11]公式：

(23)

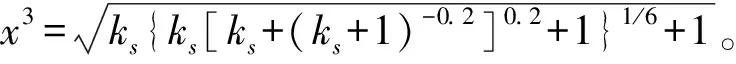
(24)

④赵延风等[5]公式：

(25)

(26)

⑤本研究公式：

(27)

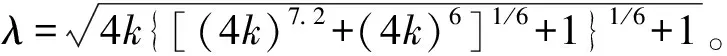
(28)

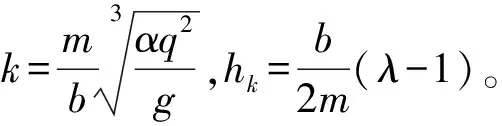
4.2 临界水深直接计算公式的误差分析

由以上的5个公式中的k值可以看出kw=ks=4k，kl=k，kz=(64k3)2，给出单位水面宽度λ=0.001～100的值，由式(9)求出λ值，进而求出λw、kl、ks、kz，再根据上述5个公式计算各自的临界水深及其相对误差，计算结果如图1所示。其中，图1-a、b为1<λ≤10和10≤λ≤100时，梯形明渠临界水深5种不同计算公式的相对误差分析结果。由于图1-b中廖云凤公式计算的相对误差随单位水面宽度λ的增加而增大，为了进一步直观分析，图1-c为10≤λ≤100时除去廖云凤[16]公式后所对应的分析结果，图1-d为1<λ≤10时刘善综[11]公式、赵延风等[5]公式和本研究公式所对应的分析结果。

图1-a、b、c和d能够清晰地反映出临界水深的相对误差变化，但要确切的分析，还需通过具体的数据加以说明。因此，表1给出了梯形明渠临界水深相对误差的计算结果。对表1进行统计和分析，得到梯形明渠临界水深计算最大和最小相对误差，结果如表2所示。

图 1 梯形明渠临界水深不同计算公式相对误差的变化

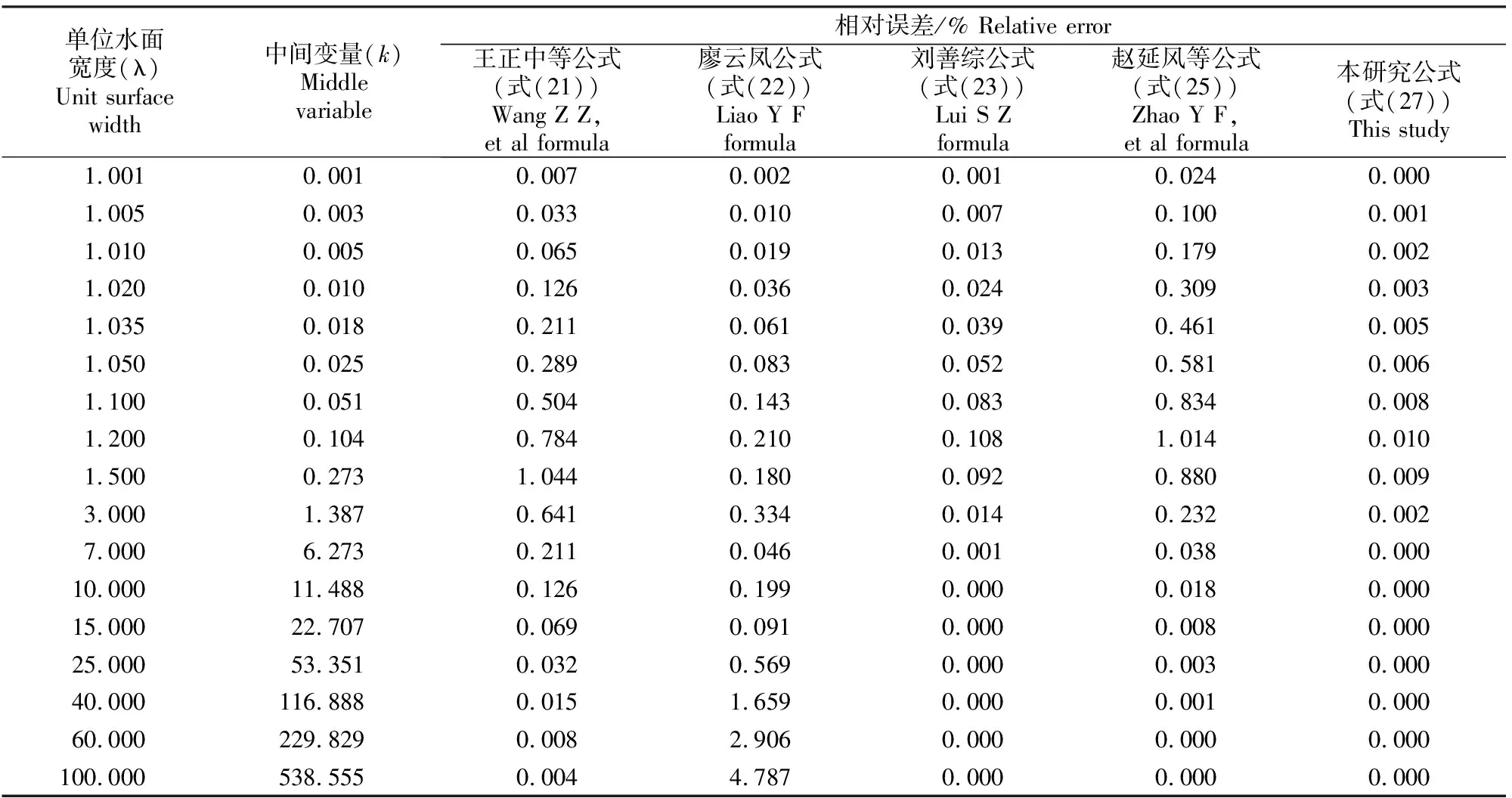
表 1 利用不同公式计算梯形明渠临界水深的相对误差比较

由表2并结合各种临界水深的直接计算公式和相对误差分析结果(图1)，从公式的简捷性、各自适用范围内的误差大小等方面进行比较，表明王正中等[3,12]公式和廖云凤[16]公式形式简单，相对误差较大；刘善综[11]公式和赵延风等[5]公式形式比较复杂，但相对误差较小；而本研究公式形式复杂，但相对误差最小。由于本研究公式精度较高，因此可用于精度要求较高的临界水深的计算。

表 2 梯形明渠临界水深5种公式计算误差分析结果(1<λ≤100)

5 结 论

在前人研究基础之上，本研究提出了新的梯形明渠临界水深直接计算公式，并对公式计算结果的相对误差进行了分析，发现在相同单位水面宽度值下，用本研究新建立的公式求得临界水深的相对误差均小于其他几个公式，最大相对误差仅为0.010%，不但适用范围广，而且还能够应用于精度要求较高的梯形明渠临界水深的计算。本研究新建立的公式虽然较其他几个公式复杂，但是借助计算器还是比较易于计算的，可用于工程实际设计中。

[参考文献]

[1] 李兴印,卢军启,杨玲霞.梯形断面明渠临界水深计算方法新探 [J].科技创新导报,2009,29(3):130-131.

Li X Y,Lu J Q,Yang L X.New study on the calculation method of critical depth of open channel with trapezoidal section [J].Science and Technology Innovation Herald,2009,29(3):130-131.(in Chinese)

[2] 苏鲁平.梯形明渠临界水深解法述评 [J].人民长江,1995,26(5):39-41.

Su L P.Commentary on solutions for critical depth in a trapezoidal channel [J].Yangtze River,1995,26(5):39-41.(in Chinese)

[3] 王正中,袁 驷,武成烈.再论梯形明渠临界水深计算方法 [J].水利学报,1999(4):14-17.

Wang Z Z,Yuan S,Wu C L.Again discussion on calculation method of critical depth for trapezoidal open channel [J].Journal of Hydraulic Engineering,1999(4):14-17.(in Chinese)

[4] 王正中,陈 涛,万 斌,等.明渠临界水深计算方法总论 [J].西北农林科技大学学报:自然科学版,2006,34(1):155-161.

Wang Z Z,Chen T,Wan B,et al.Calculation method on critical depth of open channel with trapezoidal cross section [J].Journal of Northwest A&F University:Natural Science Edition，2006,34(1):155-161.(in Chinese)

[5] 赵延风,王正中,张宽地.梯形明渠临界水深的直接计算方法 [J].山东大学学报:工学版,2007,37(6):99-105.

Zhao Y F,Wang Z Z,Zhang K D.Direct calculation method for the critical d epth of an open trapezoidal channel [J].Journal of Shandong University:Engineering Science,2007,37(6):99-105.(in Chinese)

[6] 赵延风,祝晗英,宋松柏,等.论梯形明渠临界水深的精确计算公式 [J].长江科学院学报,2009,26(4):18-21.

Zhao Y F,Zhu H Y,Song S B,et al.Discussion on the precise calculation formula of critical depth for trapezoidal [J].Journal of Yangtze River Scientific Research Institute,2009,26(4):18-21.(in Chinese)

[7] 吴持恭.水力学上册 [M].4版.北京:高等教育出版社,2008:221-224.

Wu C G.Hydraulics part 1 [M].4th edition.Beijing:Higher Education Press,2008:221-224.(in Chinese)

[8] 葛节忠,陈雪峰,黄建平.用迭代法计算明渠均匀流水深和临界水深 [J].水利水电技术,2006,37(1)：75-78.

Ge J Z,Chen X F,Huang J P.Calculation on uniform flow depth and critical depth of open channel with iterative method [J].Water Resources and Hydropower Engineering,2006,37(1)：75-78.(in Chinese)

[9] 袁镒吾.明渠梯形断面临界水深的近似计算公式 [J].应用力学学报,1992,9(2):149-152.

Yuan Y W.An approximate formula for calculation critical depth of open channel flow in trapezoidal cross-Section [J].Chinese Journal of Applied Mechanics,1992,9(2):149-152.(in Chinese)

[10] 王正中,冯家涛,胡彦华.梯形明渠临界水深计算公式的改进 [J].水利学报,1996(1):85-87.

Wang Z Z,Feng J T,Hu Y H. A method for calculating critical water depth of open channel with trapezoid section [J].Journal of Hydraulic Engineering,1996(1):85-87.(in Chinese)

[11] 刘善综.梯形渠道临界水深的计算及讨论 [J].水利学报,1995(6):83-85.

Lu S Z.Calculation and discussion of critical depth of trapezoidal channel [J].Journal of Hydraulic Engineering,1995(6):83-85.(in Chinese)

[12] 王正中.梯形明渠临界水深计算公式探讨 [J].长江科学院院报,1995,12(2):78-80.

Wang Z Z.Study on the formula of calculating critical water depth of trapezoidal channel [J].Journal of Yangtze River Scientific Research Institute,1995,12(2):78-80.(in Chinese)

[13] 徐焕文,孙慕群.梯形明渠临界水深的计算解法 [J].中国农村水利水电,2002(12):57-58.

Xu H W,Sun M Q.Calculation method of critical depth of open trapezoidal channel [J].China Rural Water and Hydropower,2002(12):57-58.(in Chinese)

[14] 刘计良,王正中,苏德慧,等.典型断面渠道临界水深计算 [J].排灌机械工程学报,2012,30(2):181-187.

Liu J L,Wang Z Z,Su D H,et al. Calculation of water critical depth in channels with common shapes [J].Journal of Drainage Irrigation Machinery Engineering,2012,30(2):181-187.(in Chinese)

[15] 王正中,芦 琴,冷畅俭,等.复式梯形断面临界水深计算公式 [J].长江科学院院报,2003,23(5):58-60.

Wang Z Z,Lu Q,Leng C J,et al.Formulaf or calculating critical depth of duplex trapezoidal open channel [J].Journal of Yangtze River Scientific Research Institute,2003,23(5):58-60.(in Chinese)

[16] 廖云凤.梯形渠道断面临界水深显示计算 [J].陕西水力发电,2001,17(4):22-23.

Liao Y F.Calculation of critical water depth for trapezoid channel cross section display [J].Shaanxi Hydroelectric Power,2001,17(4):22-23.(in Chinese)