陕北黄土坡地枣园降雨入渗产流试验与模拟

宋孝玉,白 鹏,王 娟,史文娟,王全九,4

(1 西安理工大学 西北旱区生态水利工程国家重点实验室培育基地,陕西 西安 710048；2 中国科学院 地理科学与资源研究所,北京 100101；3 河北省水利科学研究院,河北 石家庄 050051；4 中国科学院 西北农林科技大学 水土保持研究所 黄土高原土壤侵蚀与旱地农业国家重点实验室,陕西 杨凌 712100)

降雨入渗过程是土壤水循环的重要组成部分，是农业灌溉、工程设计、水文过程模拟的基础。国内外学者对土壤水分入渗过程进行了大量的研究[1-2]，建立了一系列物理基础模型和经验公式模型。国外自1911年建立概念明确、形式简单的Green-Ampt积水入渗模型以来，相继建立了Richards方程、Horton 模型、Philip模型、Smith模型等，而国内学者的研究大多是对国外经典入渗模型的改进和应用[3-4]。相对于经验入渗公式，物理模型具有明确的物理意义，便于建立其特征参数与土壤物理特征间的关系，因而得到了广泛应用[5]。在物理模型中，无论是基于Darcy定律简化的Green-Ampt模型，还是基于土壤水分运动方程解析法的Philip模型、Parlange模型等，都只适用于简单定解条件下的土壤水分运动问题，对于复杂条件的土壤水分运动问题，数值解法仍然是最客观、有效的方法[6]。

目前，Richards方程在国外广泛应用于各种水文、农业、工程施工模拟软件中，如HYDRUS[7]、SWAP[8]、SWMS-2D[9]等，国内对Richards入渗方程研究还不够重视，有限的研究大多集中在室内土柱入渗过程或点源滴灌的模拟应用方面[10-13]，在野外降雨条件下的应用研究尚比较少[14]。本研究在陕北黄土坡地人工降雨试验的基础上，采用有限差分法对Richards方程进行数值模拟求解，分析其在降雨入渗、产流过程中的应用情况，以期为该方程在该地区墒情、径流预报以及坡面侵蚀方面的应用提供参考。

1 材料与方法

1.1 试验区概况

野外降雨试验于2010-03-2011-09在陕西榆林市米脂县银州镇孟岔村红枣示范园进行，数据测试和分析于2012-12完成。米脂县位于陕西省北部，榆林市中部偏东，属无定河中游，地理位置为东经109°49′～110°29′，北纬37°39′～38°5′；总人口21.6万，其中农业人口占89.4%；总土地面积1 212 km2，川地主要种植玉米，坡地主要种植果树以及杂粮作物，在国家退耕还林的政策措施下，当地农户在坡地大面积种植果树，其中枣树种植面积最广。米脂县属典型的黄土高原丘陵沟壑区，属于温带半干旱性气候区，以无定河为分水岭，地势总体东西高中间低。试验区年降雨较少，昼夜温差较大，多年平均降雨量413 mm，主要集中在7-9月，其中最大年降雨量691 mm，最小年降雨量268.3 mm。区域土壤以黄绵土为主，土质松软，水土流失严重。试验区内种植枣树品种主要为梨枣，树龄为7～8年，株高2 m左右，株行距为2 m×3 m，栽培模式为矮化密植。

1.2 试验设计与测定方法

降雨径流试验在径流小区内进行，径流小区选择在地形、坡向、土壤、植被情况等有代表性的地段上，平整土地，去除杂草，使坡面、坡向均匀一致。考虑到人工降雨用水的便利，小区选择在离供水水源地较近的地段。根据坡面降雨入渗试验研究需要，共修建10个径流小区，坡向为阳坡，坡度测量利用全站仪进行测量。径流小区宽度均为3 m，四周用石棉瓦做防侧渗处理，埋深30～40 cm，底部修建V字形出水口，通过径流桶收集径流。供水水源位于山顶蓄水池，通过管道将用水引至径流小区，山顶蓄水池与径流小区之间垂直高度为40 m左右，人工降雨利用重力水头差进行。降雨喷头采用美国雨鸟牌1804散射型喷头，喷射半径为4 m，单喷头最大喷水量为0.8 m3/h，可通过调节阀门开度以及喷头组合方式调节降雨强度大小，经试验验证，降雨均匀度在0.8以上。试验装置见图1。

降雨径流试验在无风条件下进行，均匀布设雨量筒测定雨强。降雨历时30 min，降雨开始后，记录产流时刻。地面产流后，每间隔2 min读取1次径流筒体积，并取水样。

降雨入渗试验前，利用土钻法取土，烘干法测定土壤含水量，每隔10 cm取1次土样，每层3个重复，测定深度为1 m，取土后回填钻孔。由于坡长较短，不考虑汇流过程，入渗量根据水量平衡原理由降雨量和径流量的差值得到。

图1 降雨入渗-产流试验装置示意图

土壤水分特征用离心机测定；土壤颗粒分析用筛析法和吸管法相结合的方法测定；土壤饱和导水率在田间测定，用直径13 cm有机玻璃取田间原状土柱，取样深度约30 cm，土柱下端用细纱布固封，用马氏瓶定水头供水，待下端出水后，每隔10 min测定1次出流水量，直至出流水量恒定为止，试验重复3次。

1.3 降雨入渗产流模型及其求解

1.3.1 降雨入渗产流模型 Richards方程以达西定律和液体连续方程为基础描述非饱和土壤水分运动，对于一维垂直入渗情况，其方程形式如下：

(1)

式中：θ为土壤体积含水量，cm3/cm3；t为时间，min；z为垂直方向坐标(向上为正)；k(θ)为土壤非饱和导水率，cm/min。

1)初始条件。对于降雨入渗过程而言，初始条件为：

θ(z,0)=θ(z)。

(2)

2)上边界条件。降雨入渗初期，地表入渗能力大于降雨强度，入渗率等于降雨强度，边界为第2类边界，即有：

(3)

式中：D为土壤水分扩散率，D=KdΨ/dθ，其中Ψ为土壤基质势，cm；f为土壤入渗率。

当表层土壤水分达到饱和时，入渗率小于降雨强度，地表出现积水，上边界条件转化为第1类边界条件，即：

θ(0,t)=θ0(t)或Ψ(0,t)=Ψ0(t)。

(4)

式中：θ0(t)和Ψ0(t)分别为地表土壤含水量和基质势。

3)下边界条件。对于黄土高原坡地，地下水位极深，下边界条件为重力排水边界，相应的水分通量为下边界处的导水率，此时下边界处的含水率或基质势梯度为0，即：

(5)

式中：L为下边界深度，cm。

产流量(R)可根据水量平衡原理由降雨量(P)与累积入渗量(I)之差得到，即：

R=P-I。

(6)

非饱和导水率k(θ)一般通过Van Genuchten[15]和Mualem[16]提出的土壤水分特征曲线与非饱和导水率间的关系计算，即：

(7)

(8)

(9)

式中：Ks为土壤饱和导水率；Se为有效饱和度；θr为土壤滞留水量；θs为土壤饱和含水量；n和m为形状系数，m=1-1/n；h为土壤吸力，cm。

1.3.2 模型求解 模型采用有限差分法求解，根据土壤水分运动参数的表达式、初始条件和边界条件，按照一定的时间、空间步长进行离散，根据时段初土壤含水率预报时段末值，利用追赶法求解土壤水分运动参数的差分方程，得到时段末土壤含水率，当时段末的土壤含水量预报值与计算值的误差满足要求，则认为迭代收敛，可进入下一阶段求解。否则，以时段末的土壤含水率计算值为新的预报值，继续迭代，直至满足误差要求为止。

2 结果与分析

2.1 不同降雨强度条件下的降雨入渗产流模拟

试验在经过平整、去除杂草，且坡面、坡向均匀一致的枣树径流小区内进行，由于5月初试验地降雨量较少，枣树刚刚发芽，因此不考虑降雨截留的影响，选取初始含水率相同的3个径流小区开展不同降雨强度的人工降雨入渗、产流试验，降雨历时30 min，各场次降雨入渗、产流情况的统计结果见表1。

用1.3.1的降雨入渗、产流模型对表1不同降雨强度径流小区的试验过程进行模拟，用F1-Obs、F2-Obs、F3-Obs和Q1-Obs、Q2-Obs、Q3-Obs分别代表降雨强度为1.3,1.0,0.8 mm/min时的累积入渗量和径流实测值；以F1-Sim、F2-Sim、F3-Sim和Q1-Sim、Q2-Sim、Q3-Sim分别表示其模拟值。不同降雨强度下各径流小区的累积入渗量、径流量的实测值与模拟值见图2和图3。

表1 不同降雨强度下枣树径流小区的降雨入渗、产流情况

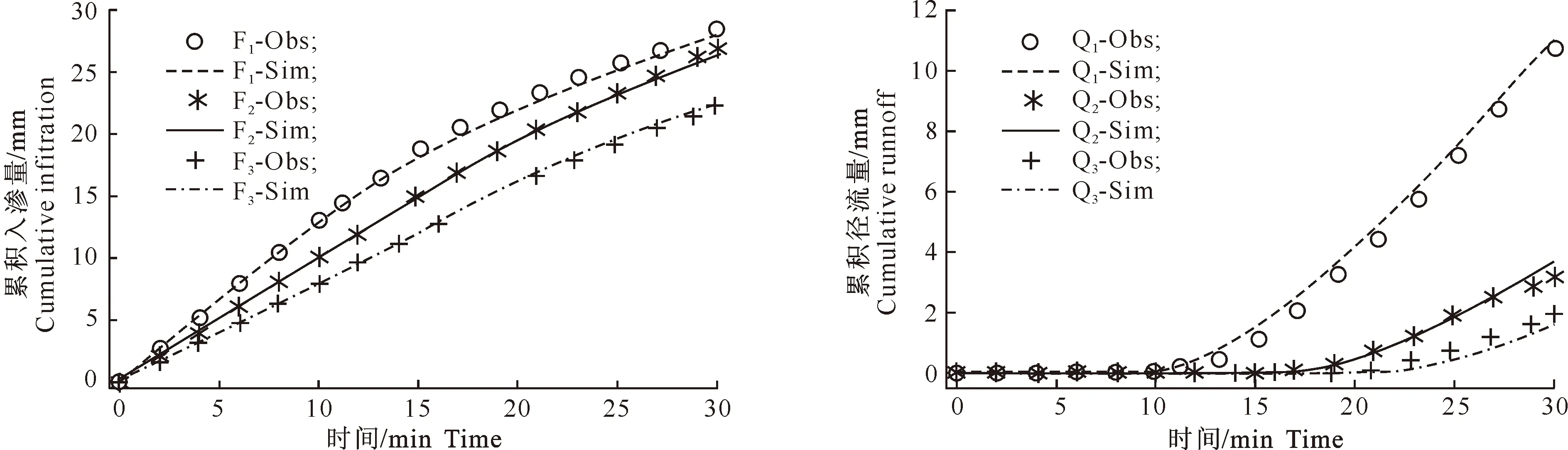
图2 不同降雨强度下径流小区累积入渗量实测值与模拟值的比较

降雨强度对土壤入渗的影响主要反映在降雨强度与土壤入渗能力的大小关系上，降雨过程中，土壤入渗能力随土壤含水率的增加而减小。降雨初始阶段，降雨强度小于土壤入渗能力，实际土壤入渗率就等于降雨强度，降雨全部入渗。随着土壤入渗能力的减小，某一时刻以后，降雨强度大于土壤入渗能力，地面开始积水。由图2，3可知，相同条件下，降雨强度越大产流时间越短，入渗达到稳定的时间也越短，累积入渗量和径流量也越大，降雨历时为30 min时，Q1-Obs是Q2-Obs的3.34倍，是Q3-Obs的6.06倍。由图2、3还可知，利用本研究建立的降雨入渗、产流模型对不同降雨强度径流小区降雨入渗、产流的模拟结果与实测值比较吻合，符合土壤实际入渗、产流规律。

2.2 不同土壤含水率条件下的降雨入渗产流模拟

为了检验模型对不同含水率条件下降雨入渗、产流的模拟效果，试验继续于5月初在枣树径流小区内进行，选取初始含水率不同的3个径流小区开展相同降雨强度(1.0 mm/min)的人工降雨入渗、产流试验，降雨历时30 min，各场次降雨入渗、产流情况见表2。

表2 不同土壤含水率下枣树径流小区的降雨入渗、产流情况

继续用1.3.1中的降雨入渗、产流模型对不同土壤含水率的试验过程进行模拟，用F1-Obs、F2-Obs、F3-Obs和Q1-Obs、Q2-Obs、Q3-Obs分别代表初始土壤含水量为0.08,0.15,0.24 cm3/cm3时的累积入渗量和累积径流量实测值；用F1-Sim、F2-Sim、F3-Sim和Q1-Sim、Q2-Sim、Q3-Sim分别代表其模拟值。得到不同土壤初始含水率条件下，3个径流小区累积入渗量、径流量实测值与模拟值，结果见图4和图5。从图4、5可以看出，土壤初始含水率对降雨入渗、产流过程有重要影响。土壤初始含水率越大，产流开始时间越早，平均入渗率越小，趋于稳定入渗的时间也越短，相同时间内，累积产流量越大，根据实测径流值可知，Q3-Obs是Q2-Obs的1.65倍，是Q1-Obs的3.35倍。由图4、5还可知，本研究的降雨入渗、产流模型对不同初始土壤含水率径流小区降雨入渗、产流的模拟结果与实测值比较吻合，符合土壤实际入渗、产流的规律。

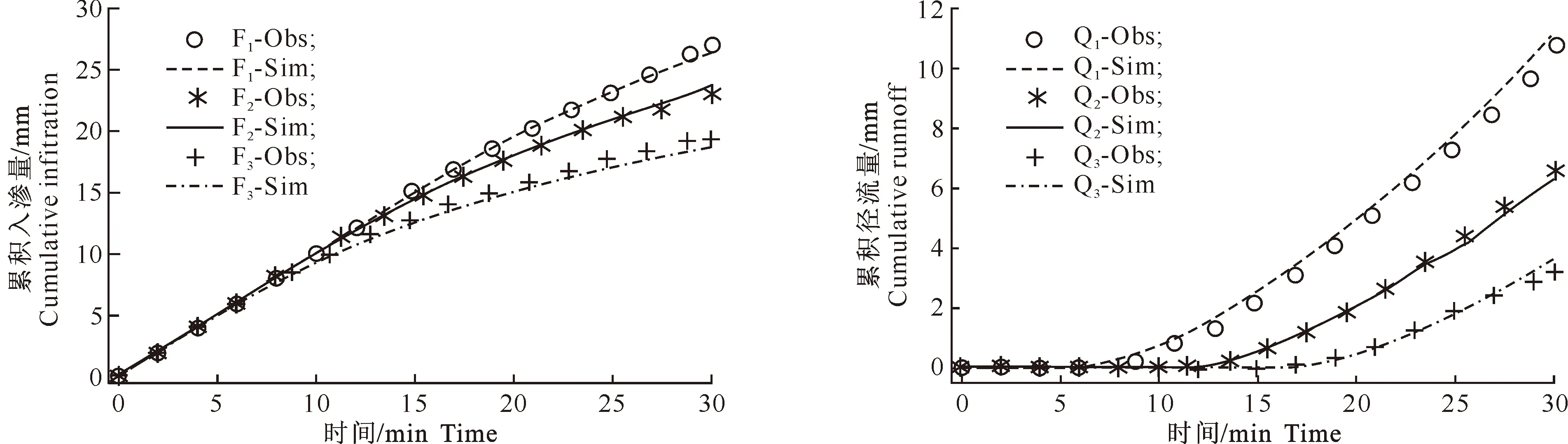
图4 不同初始土壤含水率条件下径流小区累积入渗量实测值与模拟值的比较

2.3 模型误差分析

由图2～5可知，本研究1.3.1中的降雨入渗产流模型对径流小区降雨入渗、产流数值的模拟结果与实测值比较吻合，均符合土壤实际入渗、产流的规律。为了定量分析该模型的模拟精度，对不同时刻入渗产流模拟值和实测值的误差进行分析，结果见表3。

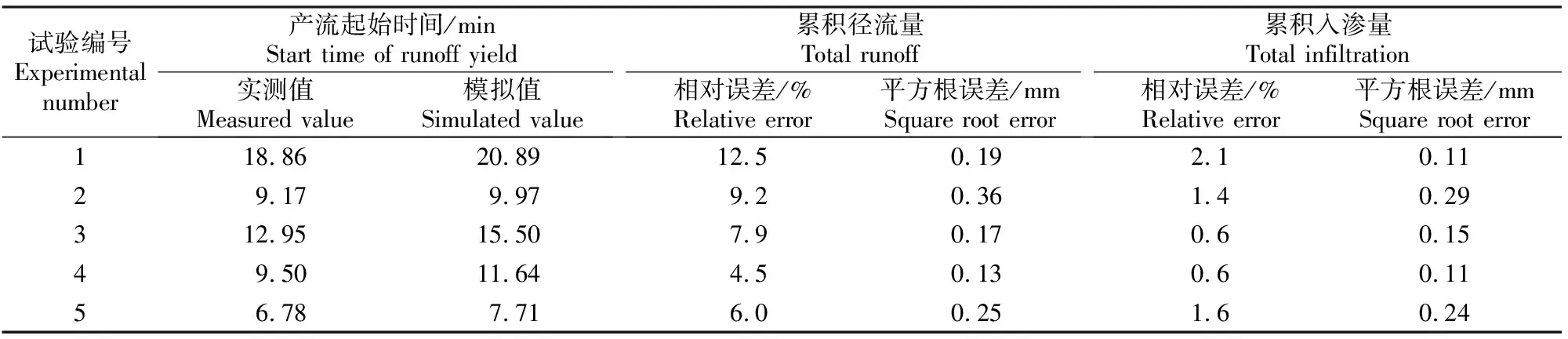
表 3 径流小区降雨入渗产流模拟值与实测值的误差分析

由表3可知，累积径流量模拟结果除试验1的相对误差为12.5%外，其余相对误差均在10%以内，所有试验的平方根误差均小于0.4 mm；累积入渗量相对误差均小于3%，平方根误差均小于0.3 mm，模拟结果比较理想。由表3还可以看出，产流起始时间的模拟值普遍滞后于实测值，滞后时间最少0.8 min，最多2.55 min，这是由坡面饱和导水率的空间变异性和降雨的不均匀性所致。由于自然界包气带土壤结构的复杂性，土壤表层体积质量以及大孔隙的空间差异都可能引起饱和导水率的不同，从而导致局部提前产流。另外，由于降雨的不均匀性，地表在雨强比较大的区域首先开始产流，这也是导致模拟产流起始时间滞后的原因之一。

3 小 结

本研究运用Richards入渗方程结合水量平衡方程模拟了黄土坡地不同降雨强度和不同土壤初始含水率条件下径流小区的降雨入渗、产流过程，通过与实测值的对比，表明该模型模拟结果合理，可作为该地区降雨入渗、产流的计算公式。

模拟产流起始时间普遍滞后于实测值，滞后时间最少0.8 min，最多2.55 min。这是由于坡面饱和导水率的空间变异性以及降雨的不均匀性引起的，关于这2种原因对产流起始时刻的具体影响规律还有待于进一步研究。

[参考文献]

[1] 王文焰，汪志荣，王全九，等．黄土中Green-Ampt入渗模型的改进和验证 [J].水利学报，2003，34(5)：30-34．

Wang W Y,Wang Z R,Wang Q J,et al.Improvement and evaluation of the Green-Ampt model in loess soil [J].Journal of Hydraulic Engineering,2003,34(5):30-34.(in Chinese)

[2] 毛丽丽，张心平，雷廷武，等．用水平土柱与Green-Ampt模型方法测量土壤入渗性能的原理与误差 [J].农业工程学报，2007，23(12)：64-68．

Mao L L,Zhang X P,Lei T W,et al.Principles and errors of measuring in-filtrability with horizontal soil column and Green-Ampt model [J].Transactions of the Chinese society of Agricultural Engineering,2007,23(12):64-68.(in Chinese)

[3] 李 毅，王全九，邵明安，等．Green-Ampt入渗模型及其应用 [J].西北农林科技大学学报：自然科学版，2007，35(2)：225-230．

Li Y,Wang Q J,Shao M A,et al.Green-Ampt model and its application [J].Journal of Northwest A&F University:Natural Science Edition,2007,35(2):225-230.(in Chinese)

[4] 梁海军，刘作新，王振营，等．地下渗灌土壤水分运动数值模拟 [J].农业工程学报，2008，24(10)：56-60．

Liang H J,Liu Z X,Wang Z Y,et al.Numerical simulation of soil water movement under infiltration irrigation [J].Transactions of the Chinese society of Agricultural Engineering,2008,24(10):56-60.(in Chinese).

[5] 王全九，来剑斌，李 毅．Green-Ampt模型与Philip入渗模型的对比分析 [J].农业工程学报，2002，18(2)：13-16．

Wang Q J,Lai J B,Li Y.Comparison of Green-Ampt model with Philip infiltration model [J].Transactions of the Chinese society of Agricultural Engineering,2002,18(2):13-16.(in Chinese).

[6] 邵明安，王全九，黄明斌．土壤物理学 [M].北京：高等教育出版社，2006：114-115．

Shao M A,Wang Q J,Huang M B. Soil physics [M].Beijing:Higher Education Press,2006:114-115.(in Chinese).

[7] Simunek J,van Genuchten M T,Sejna M.The HYDRUS-1D software package for simulating the movement of water,heat,and multiple solutes in variably saturated media,version 3.0,HYDRUS software series 1 [M].California,USA：[s.n.],2005:15-189.

[8] Van Dam J C,Groenendijk P,Hendriks R F A,et al.SWAP version 3.2：Theory description and user manual [M].Wageningen,Netherlands:Alterra,2008：11-203.

[9] Jacquesa D,J,Mallantsa D,et al.Modeling coupled water flow,solute transport and geochemical reactions affecting heavy metal migration in a podzol soil [J].Geoderma,2008,145(3/4):449-461.

[10] 周云成，何 娜，王 展，等．变水头边界条件下土壤水分运动数值模拟 [J].沈阳农业大学学报，2005,36(4):454-457．

Zhou Y C,He N,Wang Z,et al.Numerical simulation of movement of soil moisture under variable water head boundary [J].Journal of Shenyang Agricultural University,2005,36(4):454-457.(in Chinese)

[11] 李 毅，王全九，王文焰，等．入渗、再分布和蒸发条件下一维土壤水运动的数值模拟 [J].灌溉排水学报，2007，26(1)：5-8．

Li Y,Wang Q J,Wang W Y,et al.Mathematical simulation of soil water movement under infiltration,redistribution and evaporation [J].Journal of Irrigation and Drainage,2007,26(1):5-8.(in Chinese)

[12] 聂卫波，马孝义，王术礼．沟灌土壤水分运动数值模拟与入渗模型 [J].水科学进展，2009，20(5)：668-676．

Nie W B,Ma X Y, Wang S L.Infiltration model and numerical simulation of the soil water movement in furrow irrigation [J].Advances in Water Science,2009,20(5):668-676.(in Chinese)

[13] 吴梦喜．饱和-非饱和土中渗流Richards方程有限元算法 [J].水利学报，2009，40(10)：1274-1280．

Wu M X.Finite-element algorithm for Richards equation for saturated-unsaturated seepage flow [J].Journal of Hydraulic engineering,2009,40(10):1274-1280.(in Chinese)

[14] 郭向红，孙西欢，马娟娟．降雨灌溉蒸发条件下苹果园土壤水分动态数值模拟 [J].农业机械学报，2009，40(11)：68-73．

Guo X H,Sun X H,Ma J J.Numerical simulation for root zone soil moisture movement of apple orchard under rainfall-irrigation-evaporation [J].Transactions of the Chinese Society for Agricultural Machinery,2009,40(11):68-73.(in Chinese)

[15] Van Genuchten.A close-form equation for predicting the hydraulic conductivity of unsaturated soils [J].Soil Science,1980,44:892-898.

[16] Mualem Y.A new model for predicting the hydraulic conductivity of unsaturated porous media [J].Water Resource Research,1976,12(3):513-522.