激光外差干涉仪设计与实验研究

李莉君， 叶贤基， 杨 光

(华中科技大学 物理学院 物理实验中心， 湖北 武汉 430074)

精密测量主要用于机械制造、材料和器件的结构与性能测试、空间测距等方面[1]。运用光学方法实现精密测量是其中重要的方法之一，常见的有迈克耳孙干涉仪、法-珀干涉仪及激光外差干涉仪。前两种干涉法均采用正向入射方式, 测量精度约为100 nm[2]。目前，高精度的激光干涉仪大多为激光外差干涉仪，产生双频激光的方法主要是利用塞曼效应或声光移频器。塞曼效应受频差闭锁现象影响，产生的双频频差一般较小，通常最大频差不超过4 MHz。声光调制方法得到的频差通常较大，一些产品双频激光频差达到20 MHz以上[3-4]。

双频激光干涉仪是直接测量两个信号的相位差来决定位移的。这种位移(亦即光程差)信息载于两种频率光束干涉后产生的拍频信号中。因此，对由光强变化引起的直流电平变化不敏感，所以抗干扰能力强，常用于高精度直线度测量、平面度测量和小角度测量[5]。

本文的实验方案设计采用物理实验中常见的激光器、光学晶体及声光移频器，利用声光调制产生两束固定频差的激光，组建出一套构成简洁及方便调试的激光外差干涉仪。运用实验装置观察到了激光双频干涉现象，并进行了微小位移测量。

1 双频激光外差干涉仪的光路设计

实验中设计的双频激光外差干涉仪光路如图1所示。其测量原理：氦氖激光器输出的激光光束通过分光镜BS1分成两束，分别经过声光移频器AOM产生频率为f1和f2的光束。两束光再分别通过分光镜BS2和BS4各自分成两束，频率f1和f2的光束经过分光镜反射后产生干涉，形成参考光束，并通过光电探测器PD1接收干涉信号。另外，透过BS2和BS4的f1和f2的光束分别通过反射镜M1和M2，当位于测量臂上的反射镜M2移动时，测量臂(BS4到M2的距离)光程变化导致测量光束的相位发生变化，因而干涉后的拍频测量信号的相位也发生变化，此测量信号由光电探测器PD2接收[6]。

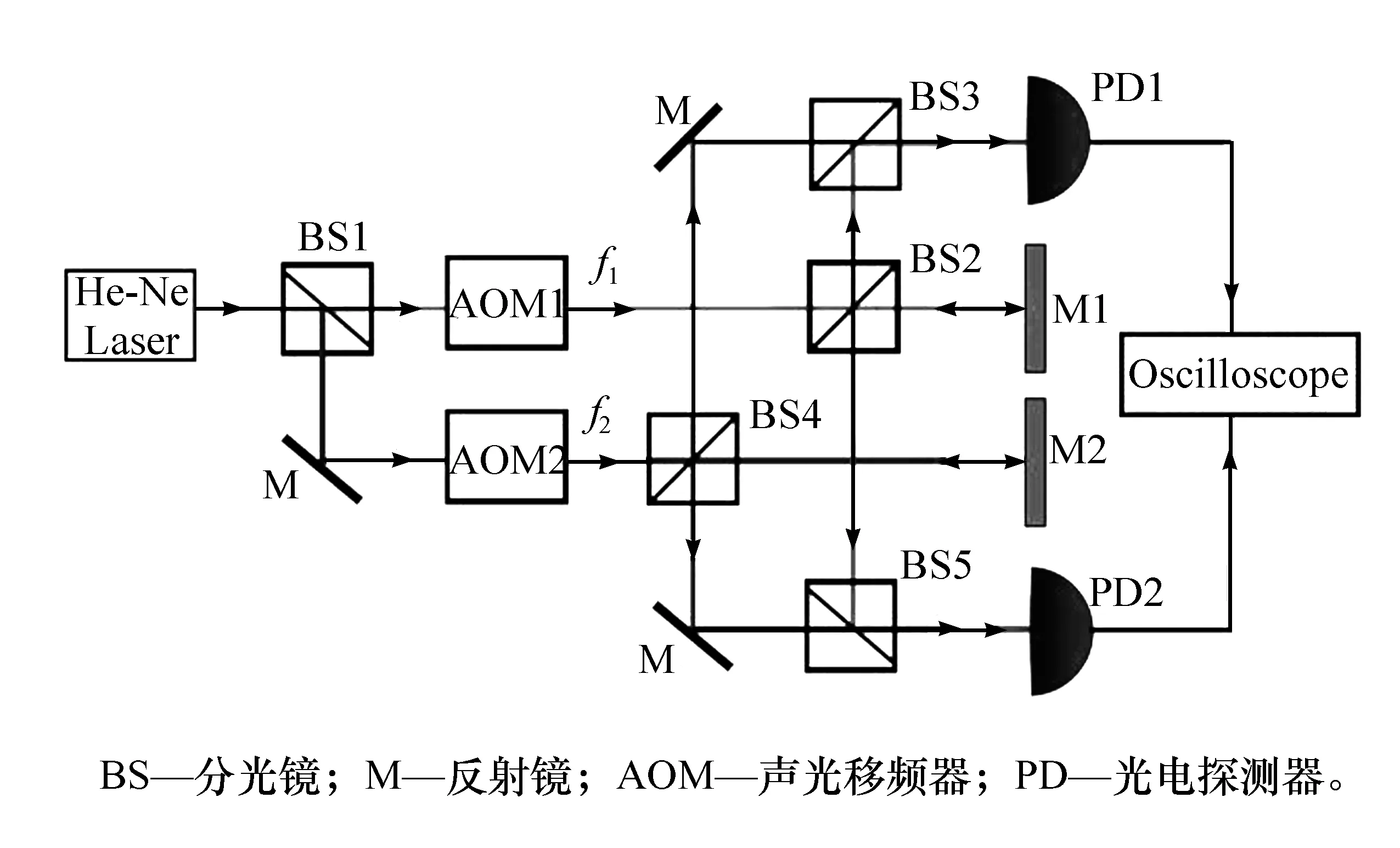
图1 非偏振双频激光外差干涉系统

在本实验系统中，给压电陶瓷施加直流电压以驱动M2运动，从而产生微小位移。通过示波器比较参考光束信号和测量光束信号的相位差，即可得出干涉仪两臂光程差的变化量和可动反射镜的位移量。

各个主要器件的参数为：

(1) He-Ne激光器作为光源，中心波长为632.8 nm，光功率为0.5 mW；

(2) 两声光移频器的输出频率分别为80 MHz和82 MHz，产生一级衍射后的两列光束的频率差为2 MHz左右；

(3) 压电陶瓷选用PI公司的P-885.10型号，外加100 V电压时，标称位移为6.5(1+0.2)m；

(4) 分光晶体的分光比为50%。

2 双频外差干涉仪的测量原理

利用单频光的光场来讨论双频外差干涉仪的测量原理。设He-Ne激光器的输出光为

E=E(t)sin[ω0t+φ(t)]

(1)

φ(t)为激光器的随机相位扰动函数，ω0为激光角频率，E(t)为激光幅度[7]。

对于参考光束，频率f1和f2的电场可表示为：

E1(t)=α1E(t)sin[ω0t+φ(t)+φ1+2πf1t]

(2)

E2(t)=α2E(t)sin[ω0t+φ(t)+φ2+2πf2t]

(3)

式中:φ1为光束经过分光镜BS1、AOM1、BS2和BS3后产生的相位变化；φ2为光束经过分光镜BS1、AOM2、BS4和BS3后产生的相位变化;α1和α2是与分光晶体的衍射效率等物理量有关的系数。

PD1探测到参考光束的光强IPD1为

IPD1=η|[E1(t)+E2(t)] [E1(t)+E2(t)]*|

=η[I1(f1)+I2(f2)+I3(f1+f2)+I4(f1-f2)]

(4)

η为PD的光电转换效率。

由于一般的光电探测器不能响应高频项f1、f2及f1+f2，因此这3个频率对应的光强I只能输出随时间的平均值，为直流量[8]。最后一项|f1-f2|为干涉项，是两束激光干涉形成的拍频信号，其被探测器接收的光强信号为

IPD1∝I0cos[2π(f2-f1)t+φ′]

(5)

式中φ′是两束激光在分光晶体等光学器件的产生相位差。

对于测量信号，反射镜M2的移动产生了光程变化，因此干涉信号便产生了额外的光程差，其光强为

IPD2∝I0cos[2π(f2-f1)t+φ1+Δφ]

(6)

当频率f1和f2相差不大时，可认为两束激光波长相等,12，比较参考信号和测量信号的相位，从而得出相位差为

(7)

实验中采用示波器比较参考信号和测量信号的相位差得出光程差，继而可以得出反射镜M2的移动量。

3 实验结果与分析

3.1 参考信号与测量信号

将2个声光移频器的输出频率分别设置为80 MHz和82 MHz，则参考信号频率应为2 MHz。由示波器显示的参考信号(图2中的上信号,1通道信号)的频率也在2 MHz左右，与理论符合。

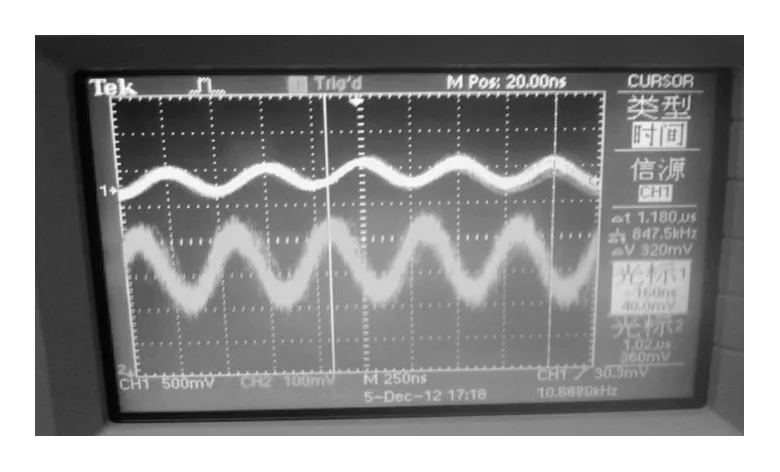
图2 参考信号(上)与测量信号(下)

由0 V开始,每隔2.5 V逐渐增加压电陶瓷上的驱动电压，记录测量信号(图2中2通道信号)与参考信号的相位差，由关系式(7)可以计算出不同电压值对应的压电陶瓷位移量。

3.2 压电陶瓷的压电系数测量

测得的位移与驱动电压的数据见表1,关系曲线见图3。

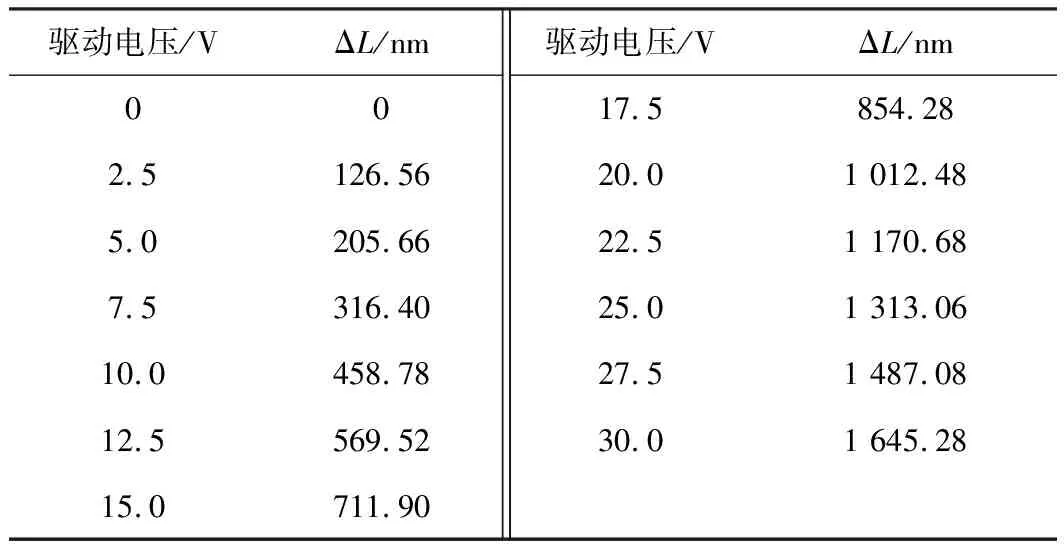
表1 驱动电压与位移的关系

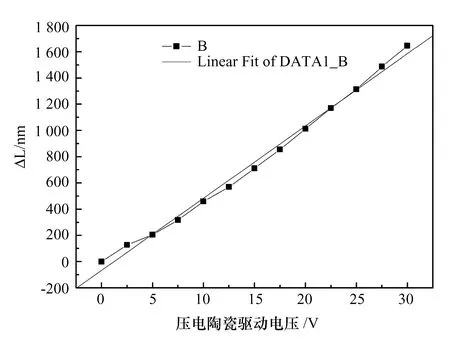
图3 压电陶瓷位移与驱动电压的关系曲线

经线性拟合得到位移与驱动电压的关系式为

4 结束语

介绍了激光双频干涉的实验原理，运用自行组建的实验装置观察了激光双频干涉现象，并利用压电陶瓷进行了微小位移的测量，在现有测量方案下测量精度在30 nm左右。将精密测量的实验应用于本科生的实验教学课程中，有助于培养学生的科学研究能力和良好的实验习惯[10]。从实验过程及测量结果来看，该激光双频干涉实验装置对外界环境影响，尤其是光学平台的震动比较敏感，实验周围环境的清洁、干燥、安静是提高测量精确度的有效途径[11-12]。此外，实验的误差方面还有诸多方面的问题有待深入研究。

[1] 张忠萍, 杨福民. 卫星激光测距的新进展[J]. 天文学的进展, 2001,19(2):283-288.

[2] 严雪飞,蔡晗,熊永红等.纳米级光纤位移传感器[J].物理实验,2011,31(6):17-21.

[3] 李醒飞,王驰,向红标，等.光学外差干涉法检测微弱超声振动[J].光学精密工程,2008, 16(7):1158-1162 .

[4] 赵洋,周挺,李达成.外差干涉仪中声光调制器特性对测量精度的影响[J].光学学报,1999,19(10):1368-1374.

[5] 尤政.光外差相位测量技术[J]. 计量技术,1995(5):78-83.

[6] 周小珊,李岩. 相位激光测距与外差干涉相结合的绝对距离测量研究[J].应用光学,2010,31(6):1013-1017.

[7] 周炳琨,高以智,陈家骅.激光原理[M].北京:清华大学出版社,1995.

[8] 姚建铨,于意仲.光电子技术[M].北京:高等教育出版社,2006.

[9] 汪友生,徐小平.相位法激光测距的实现[J].北京工业大学学报, 2003,29(4):424-427.

[10] 王永强,刘太刚.空间光调制器简介及其应用[J]. 焦作大学学报, 2007(3):230-232.

[11] 赵慧洁,张广军.影响激光外差高精度计量的几个关键因素[J].北京航空航天大学学报，2002,28(2):221-224.

[12] 郑义明,保铮. 一种改进的相位误差估计算法[J].西安电子科技大学学报, 2001,28(4):472-477.