鄂尔多斯盆地山西组二段煤层对下伏砂岩地震反射特征影响的数值模拟分析

赖生华,梁全胜,袁通路

(1.西安石油大学,陕西西安710065;2.陕西延长石油(集团)有限责任公司,陕西延安716000)

自Widess[1]基于砂岩楔状模型研究砂岩顶、底面地震反射波叠加干涉特征以来,如何利用地震反射信息预测薄层砂岩分布一直是学者们关注的研究课题。基于砂岩顶、底面反射系数相等且符号相反的假设条件,Widess[1]通过砂岩楔状模型的正演研究提出了薄层地震反射波叠加干涉理论,并给出了薄层(厚度小于λ/4,λ为地震波长)地震反射振幅与地层厚度关系的线性表达式。因此,利用薄层地震反射振幅与厚度基本具有线性关系的规律,可以预测薄层砂岩的厚度[1-2]。Kallweit等[3]总结了零相位子波特征后也认为,砂体厚度等于λ/4时,复合波的反射振幅达到最大值;随着砂体厚度减小,振幅也随之减弱。有的学者通过研究薄互层地震调谐作用,认为子波干涉后形成的单个复合波反射振幅与砂层累计厚度成正相关关系,而多个复合波反射振幅与砂层厚度不一定具有正相关性[4-6]。

由Widess[1]的理论可知,不同相位地震子波具有不同的叠加干涉特征,因而具有不同的地震反射特征。长期以来,零相位子波被认为是适用于地震解释的最佳子波。早在1961年,Sengbush等[7]就指出零相位子波的分辨率极限大约是主波长λ的1/4。Wood[8]总结了零相位子波的特征,讨论了用零相位子波代替震源子波的基本原理。Brown[9]则总结了零相位子波的许多优点,但是他同时也指出零相位子波优于其它子波的假设是建立在地震反射必须来自于单一界面,或者地震数据具有足够高的分辨率,可以分辨来自地层顶和底的单个反射的基础之上的。Yilmaz[10]进一步讨论了用零相位子波代替震源子波而不改变其振幅谱的子波处理方法的基本原理。黄军斌等[11]则研究了零相位地震子波旁瓣对薄砂岩识别的影响。

现今的地震岩性学解释研究多是基于Widess模型,提出了一系列的认识、技术和方法。但Widess提出的薄层地震反射波叠加干涉理论只适用于砂岩顶、底面反射系数相等且符号相反的理想假设情况,与实际地质情况相差甚远。在实际地下环境中,砂岩储层顶、底面反射系数有着明显的差异,研究来自薄储层的地震反射特征不仅要考虑薄层本身,而且要考虑上覆、下伏地层阻抗不同所产生的地震响应特征[1,12]。特别是在含煤岩系中,煤层对下伏砂岩地震干涉作用强,这对砂岩地震反射振幅、频率及极性都会产生强烈的影响,导致砂岩地震响应与地层岩性的对应关系更为复杂。但从已发表的研究资料来看,目前开展这方面研究的文献尚不多见。

我们针对鄂尔多斯盆地二叠系山西组二段(山2段)含煤岩系中煤层对下伏砂岩地震响应的强烈干涉作用,建立地质模型开展正演模拟分析,从理论上研究煤层的厚度和位置对下伏砂岩地震反射特征的影响,对Widess理论进行修正,得出含煤岩系中砂岩地震响应与地层岩性对应关系的规律性认识,为含煤岩系或相似地球物理环境的地震岩性解释提供理论基础。

1 正演模型建立与模拟分析方法

1.1 建模靶区地震地质概况

鄂尔多斯盆地二叠系山2段为浅水型三角洲下三角洲平原沉积环境[13-15],煤层发育,常形成“泥岩—煤层—砂岩—泥岩”或“泥岩—煤层—泥岩—砂岩—泥岩”沉积序列,砂岩中天然气储量丰富,为天然气主力产层。由于煤层声波传播速度低,与上、下砂岩或泥岩地层阻抗差异明显,常形成强振幅、高连续的地震反射同相轴。

早二叠世山西期,受满蒙洋壳向华北克拉通板块俯冲作用加剧的影响,鄂尔多斯盆地山西组发育了一套浅海陆棚基础上的三角洲沉积[14-17]。其下部主要为灰色、浅灰色薄层状砂岩与深灰、灰黑色泥岩不等厚互层,夹薄层状煤层;上部为灰色、深灰色泥岩与灰色砂岩、含砾粗砂岩以及少量细砾岩不等厚互层,偶夹炭质泥岩或煤层[17]。通过观察煤层在野外露头上的分布及井下煤层横向对比,山2段煤层虽然具有不同的空间分布样式,但总的说来可以归纳如下：煤层直接上覆于砂岩或煤层与砂岩相距一定距离,分别呈现为“泥岩—煤层—砂岩—泥岩”、“泥岩—煤层—泥岩—砂岩—泥岩”沉积序列(图1)。根据声波和密度测井资料统计分析,鄂尔多斯盆地二叠系山2段砂岩、泥岩及煤层的平均纵波传播速度分别为4347,4000,3100m/s。由于鄂尔多斯盆地山2段压实作用强烈,砂岩、泥岩的平均密度相近,为2.44g/cm3;煤层平均密度为1.66g/cm3。

含煤岩系中煤层对下伏砂岩地震干涉作用强,这对砂岩地震反射振幅、频率及极性都会产生强烈影响,地震反射同相轴的极性与地层岩性的对应关系更为复杂。山2段含煤岩系中的地震响应-地层岩性关系与基于Widess理论得出的认识有很大的区别。根据现今的认识,尚不能精确预测该地区厚度小于λ/4的薄层砂岩的空间展布。

1.2 正演地质模型设计与建立

根据鄂尔多斯盆地二叠系山2段煤层分布特征构建了两个地质模型,分别用于研究上覆煤层厚度变化和位置变化对下伏砂岩地震反射特征的影响。模型一共4层,楔状煤层(厚度0～10m)直接上覆于厚度30m的层状砂岩(图2a),第1层和第4层均为泥岩层,用于表征“泥岩—煤层—砂岩—泥岩”岩性结构。模型二共5层,稳定煤层与30m厚度的层状砂岩之间夹0～100m厚度渐变的泥岩层(图2b),第1层和第5层均为泥岩层,用于表征“泥岩—煤层—泥岩—砂岩—泥岩”岩性结构。模型中砂岩、泥岩及煤层的纵波速度和密度的取值见上节所述。

图1 鄂尔多斯盆地二叠系山2段煤层分布特征

1.3 正演模拟及分析方法

正演数值模拟选取主频为5～120Hz(频率变化步长为5Hz)的零相位Ricker子波,采用子波与反射系数褶积的理论模型,采样间隔为1ms,生成不同主频激发子波的模型一和模型二的二维合成地震剖面。

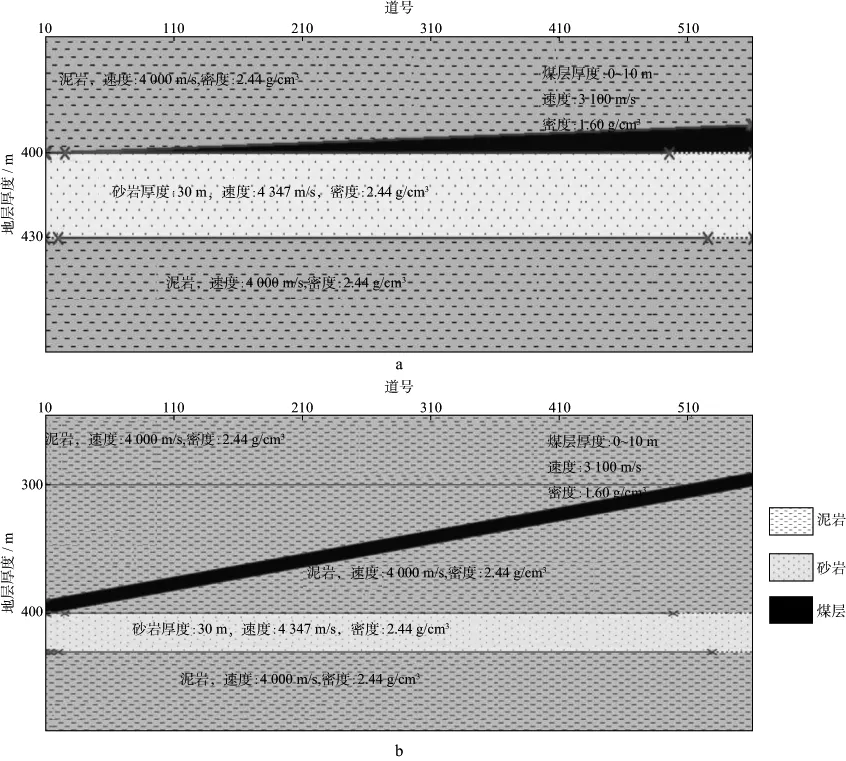
图2 正演地质模型一(a)和模型二(b)

Widess[1]采用基于砂岩顶、底面反射系数相等且符号相反假设条件的砂岩楔状模型,通过正演研究提出了薄层地震反射波叠加干涉理论：当地层厚度大于地震波长λ时,来自砂岩顶、底界面的反射子波在时间域内完全分离,这种记录反映了两个界面的最大可能信息。当地层厚度减薄至小于λ时,来自顶、底界面的地震反射子波逐渐产生叠加;当地层厚度为λ/ 4或更薄时,实际上留下的都是顶、底地震反射子波叠加产生的信息,即分辨不出单个顶、底界面反射的信息。基于地震反射特征,Widess定义地震意义上的薄层厚度d(双程时间厚度td)小于λ/4时,来自薄层的地震反射振幅为

(1)

式中：A为顶、底无干涉时的反射振幅。

我们通过提取模型一和模型二对应的合成地震记录中砂岩顶、底界面反射波振幅进行详细分析,并与Widess的理论认识进行比较,以分析不同厚度及不同位置的煤层对下伏层状砂岩地震反射极性及反射振幅的影响。

2 煤层厚度对砂岩地震反射特征的影响

利用模型一(图2a)可以分析煤层厚度变化对下伏砂岩地震反射特征的影响。图3是基于20Hz零相位Ricker子波得到的模型一的正演地震剖面。图4a给出了模型一中上覆煤层厚度稳定情况下,子波频率变化对砂岩顶、底界面反射振幅的影响;图4b则给出了子波频率稳定情况下,上覆煤层厚度变化对砂岩顶、底界面反射振幅的影响。模型一中自上而下3个界面反射系数分别为-0.326,0.363,-0.042;煤层尖灭处反射系数为0.042。煤/砂岩界面反射系数高于砂岩/泥岩界面反射系数,因此,煤/砂岩界面(砂岩顶面)地震反射强度较砂岩/泥岩界面(砂岩底面)地震反射强度大(图4)。

2.1 煤层厚度及子波频率对下伏砂岩顶面地震反射特征的影响

建模靶区山2段煤层平均厚度d约为1.2m(双程时间厚度为0.8ms),理论调谐频率为323Hz。若地震子波主频为5Hz,则主波长λ=620m(煤层纵波速度为3100m/s),d/λ=1/517;若地震子波主频增高至120Hz,则主波长降低至26m,d/λ=1/22。根据公式(1),1.2m厚煤层在5Hz主频零相位Ricker子波作用下产生的地震反射振幅大致为0.02A,而在120Hz主频零相位Ricker作用下产生的振幅大致为0.57A。这说明即使煤层很薄,在高频子波作用下,其所产生的振幅也较强。若煤层厚度为10m(双程时间厚度为6.6ms),则理论调谐频率为39Hz,在5Hz主频的零相位Ricker作用下产生的地震反射振幅约为0.2A。这说明厚煤层在低频子波作用下,也会产生一定程度的地震反射能量。

图3 模型一的20Hz零相位Ricker子波正演地震剖面

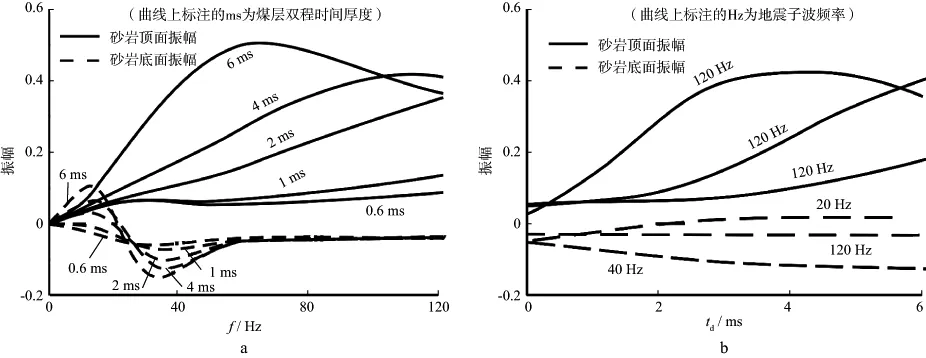
图4 子波频率f变化(a)和上覆煤层厚度(双程时间厚度td)变化(b)对模型一中砂岩顶、底界面反射振幅的影响

根据上述分析可以认为,在煤层较薄、地震子波频率较低的情况下,煤层顶、底面地震反射波形成相消干涉,煤层产生很弱的地震反射,对下伏砂岩顶面地震反射基本没有什么影响;但在子波频率较高时,薄煤层也会产生一定的地震反射强度,导致下伏砂岩顶面地震反射振幅增加。在煤层较厚、地震子波频率较高的情况下,煤层将会产生强烈的地震反射,这将会极大地增强砂岩顶面地震反射振幅;但在子波频率较低情况下,煤层也会产生一定的地震反射,在一定程度上增强下伏砂岩顶面地震反射(图4)。

当煤层厚度稳定时,砂岩顶面地震反射振幅随子波频率增加而增加,直至达到调谐频率(即调谐振幅对应的频率)(图4a)。而对于相同厚度的下伏砂岩来说,即使在相同子波频率条件下,其顶面地震反射振幅也会随煤层厚度增加而增加,直至达到砂层的调谐振幅(图4b)。但不论频率怎么变化,砂岩顶面反射始终位于波峰,不会产生极性反转。这说明在上覆煤层厚度发生变化时,不能用下伏砂岩顶面地震反射振幅来预测薄层砂岩厚度(图4b)。

2.2 煤层厚度及子波频率对下伏砂岩底面地震反射特征的影响

模型一中砂岩底面为砂岩/泥岩接触界面,由图4可以看出,煤层对砂岩底面地震反射特征的影响主要是由地震干涉作用导致的。相对砂岩顶面而言,上覆煤层对砂岩底面地震反射影响较弱。当子波频率高于55Hz时,不论上覆煤层厚度怎么变化,地震波能够分开砂岩顶、底面,煤层对砂岩底面地震反射基本没有影响(图4a)。

当煤层厚度薄于1.5m(双程时间厚度1.0ms)时,上覆煤层地震反射能量弱,煤层对砂岩底面地震反射基本不会产生影响。对于厚度大于3m(双程时间厚度2.0ms)的上覆煤层,低于55Hz的地震子波频率将会对砂岩底面地震反射产生强烈影响。特别是子波频率低于20Hz时,泥岩/煤、煤/砂岩及砂岩/泥岩界面地震反射产生相强干涉,并使砂岩底面形成波峰地震反射同相轴(极性发生反转)(图3)。当子波频率为20～55Hz时,虽然来自模型一的几个界面的地震反射波仍然产生强烈的干涉作用,对砂岩底面地震反射有较大影响,但振幅仍然为负值,不会导致极性反转(图4a)。

对于相同厚度的下伏砂岩,即使在相同子波频率条件下,砂岩底面地震反射振幅也会随煤层厚度增加而增加(绝对值),直至达到调谐振幅。这反映了在上覆煤层厚度发生变化时,也不能用下伏砂岩底面地震反射振幅来预测薄层砂岩厚度(图4),这与砂岩顶面情况一致。

综上所述,在煤层上覆于砂岩的情况下,煤层对砂岩顶面地震反射影响更强。不论煤层厚度和地震子波频率怎样变化,砂岩顶面始终位于地震波峰反射同相轴,这与前人的研究成果一致[12,18-20]。但是,当地震子波主频低于20Hz时,砂岩底面地震反射同相轴的极性可能发生反转(与上覆煤层厚度有关)。当上覆煤层厚度不稳定时,砂岩顶、底面地震反射振幅既不能反映薄层(小于λ/4)也不能反映厚层(大于λ/4)砂岩的厚度,即不能利用砂岩顶面地震反射振幅预测薄层(小于λ/4)砂岩厚度,这比基于Widess模型得出的认识更复杂。上覆煤层厚度不变时,利用砂岩顶、底面地震反射最佳频率(最厚砂岩的调谐频率)的振幅信息可以预测薄层砂岩的厚度。当上覆煤层厚度大于3m(双程时间厚度2.0ms)时,只能利用砂岩顶面地震反射振幅来预测砂岩厚度,但当煤层厚度薄于3m时,也可以利用砂岩底面地震反射振幅信息来预测薄层砂岩的厚度(图4)。

3 煤层位置对砂岩地震反射特征的影响

利用模型二可以分析煤层位置对砂岩反射特征的影响。模型二(图2b)中,10m厚度煤层上覆于30m厚度的砂岩之上;煤层与砂岩之间夹0～100m厚度渐变的泥岩,表征煤层距砂岩的位置逐渐变化。模型中自上而下4个界面反射系数分别为-0.326,0.326,0.042,-0.042;泥岩尖灭处反射系数为0.363。图5a是45Hz零相位Ricker子波得到的模型二的正演地震剖面;图5b是10Hz零相位Ricker子波得到的模型二的正演地震剖面。图6a给出了上覆煤层与层状砂岩间距离稳定(泥岩夹层厚度不变化)情况下,子波频率变化对砂岩顶、底界面反射振幅的影响;图6b则给出了子波频率稳定情况下,上覆煤层与层状砂岩间距离变化对砂岩顶、底界面反射振幅的影响。

图5 模型二的45Hz(a)和10Hz(b)零相位Ricker子波正演地震剖面

图6 子波频率变化(a)和上覆煤层与层状砂岩间距离变化(b)对模型二中砂岩顶、底界面反射振幅的影响

当稳定煤层与下伏砂岩之间的距离逐渐变化时(煤层与砂岩间夹楔状泥岩),实际上就反应了煤层相对于下伏砂岩的位置不断发生变化。由于煤层对砂岩顶、底面地震反射特征的影响不一致,砂岩顶、底面地震反射振幅曲线出现严重的不对称(图6)。与不含煤层的情况及Zeng等[21-22]的研究成果比较,该模型揭示了地层岩性与地震反射同相轴极性之间具有更复杂的关系。

3.1 煤层位置及子波频率对下伏砂岩顶面地震反射特征的影响

当煤层向砂岩靠近,与砂岩之间的间距小于20m(双程时间厚度10.0ms)时,煤层主要使砂岩顶面地震反射振幅增强(绝对值)。但当煤层远离砂岩,与砂岩之间的间距大于50m(双程时间厚度25.0ms),并且地震子波频率高于40Hz时,泥岩顶、底面地震反射波不会产生干涉作用,煤层对砂岩顶面地震反射没有影响(图6a)。

随着煤层越来越靠近砂岩(煤层与砂岩之间的泥岩夹层变薄),地震波在泥岩夹层中的旅行时间逐渐缩短,下伏砂岩的调谐频率逐渐升高(图6)。在该模型中,要使煤层顶、底面地震反射波不叠加产生干涉作用,地震子波频率必须高于155Hz,即在模拟频率区间内(低于120Hz),煤层顶、底面地震反射波始终存在干涉现象。根据模型二估算不同调谐频率下薄砂层的地震反射振幅(表1),可见砂岩调谐频率均低于对应上覆泥岩调谐频率。在砂岩达到调谐频率时,泥岩顶、底面地震反射波仍会产生叠加干涉,即相对于砂岩的调谐频率(即砂岩调谐振幅对应的频率),上覆煤层和泥岩都是地震意义上的薄层。这说明,在低于砂岩调谐频率时,地震波不能有效分辨煤层、泥岩夹层和砂岩顶、底面,即在达到砂岩调谐频率时,砂岩顶面振幅也包含有上覆煤层及泥岩的振幅信息。根据Widess公式,可以近似估算达到砂岩调谐频率时,薄砂层的地震反射振幅。结果表明,随着煤层距砂岩顶面越近,砂岩调谐振幅越来越强(表1,图6)。

在相同的地震子波频率条件下,当上覆煤层距砂岩的位置发生变化时,砂岩顶面地震反射同相轴可能会发生极性反转(图6)。比如在地震子波频率为35～65Hz的情况下,当煤层与砂岩相距20m(双程时间厚度10.0ms)左右时,泥岩顶、底面地震反射波波谷旁瓣发生叠加,形成一个复合波谷,表现为砂岩顶面地震反射同相轴极性发生反转(图5a)。随着地震子波频率增高,在煤层越靠近砂岩(上覆泥岩越薄)的地方的砂岩顶面发生地震同相轴极性反转。如当子波频率为10Hz时,在上覆泥岩厚度约为60m(双程时间厚度30.0ms)的砂岩顶面产生地震同相轴极性反转(图5b);而当子波频率增加到95Hz时,则在煤层更加靠近砂岩,上覆泥岩厚度薄于6m(双程时间厚度3.0ms)的砂岩顶面产生地震同相轴极性反转。

表1 依据模型二估算的不同调谐频率下薄砂层的地震反射振幅

注：A为地层顶、底面无干涉时的反射振幅。

3.2 煤层位置及子波频率对下伏砂岩底面地震反射特征的影响

与砂岩顶面比较,模型二中上覆煤层对砂岩底面地震反射影响相对较弱。当子波频率超过55Hz时,不论煤层位置(泥岩夹层厚度)怎么变化,上覆煤层对砂岩底面地震反射基本没有影响(图6)。地震子波频率为20～55Hz时,砂岩底面地震反射增强,但不会导致地震反射同相轴极性发生反转(图5b)。当地震子波频率低于20Hz,由于煤层位置(泥岩夹层厚度)的变化,上覆煤层可能使砂岩底面地震反射减弱、增强或导致砂岩底面反射同相轴发生极性反转(图6)。如在地震子波频率为14Hz时,当泥岩夹层厚度约为20m(双程时间厚度10.0ms)时,该模型中砂岩底面地震反射振幅比Widess模型中砂岩底面地震反射振幅降低了30%(绝对值);但当煤层向砂岩靠近,上覆泥岩厚度薄于10m(双程时间厚度5.0ms)时,则砂岩底面位于地震反射波峰同相轴,发生极性反转。模拟结果表明,当煤层远离砂岩,与砂岩之间的距离超过80m(双程时间厚度40.0ms)时,上覆煤层对砂岩底面地震反射基本不会产生影响(图6)。

综上所述,当煤层距砂岩的位置发生变化时,砂岩顶、底面地震反射振幅不能反映砂岩厚度变化。在上覆泥岩夹层厚度不变的情况下,当上覆煤层与砂岩之间的距离小于20m(双程时间厚度10.0ms)时,应利用砂岩顶面地震反射最佳频率的振幅信息来预测薄层砂岩厚度;当上覆煤层与砂岩之间的距离大于80m(双程时间厚度40.0ms)时,应利用砂岩底面地震反射最佳频率的振幅信息来预测薄层砂岩厚度(图5,图6)。

4 结论与认识

基于鄂尔多斯盆地二叠系山2段含煤岩系实际地质情况所建立的地质模型的正演模拟分析,从理论上研究了上覆煤层的厚度和位置对下伏砂岩地震反射特征的影响,得出了含煤岩系中砂岩地震响应与地层岩性对应关系的规律性认识。

1) 不论煤层厚度和地震子波频率怎样变化,砂岩顶面始终位于地震波峰反射同相轴,不会使得地震反射同相轴极性发生反转。但是,当地震子波频率低于20Hz时,砂岩底面地震反射同相轴的极性可能发生反转(与上覆煤层厚度有关)。

2) 当煤层靠近砂岩,与砂岩之间的间距小于20m(双程时间厚度10.0ms)时,煤层使砂岩顶面地震反射增强。但当煤层远离砂岩,与砂岩之间的间距大于50m(双程时间厚度25.0ms),在地震子波频率高于40Hz时,煤层对砂岩顶面地震反射没有影响。煤层位置变化可以使砂岩顶面地震反射同相轴可能会发生极性反转。随着地震子波频率增高,则在上覆泥岩越薄的地方(煤层距砂岩越近的地方)的砂岩顶面发生地震反射同相轴极性反转。

3) 当地震子波频率超过55Hz左右时,不论煤层位置怎么变化,煤层对砂岩底面地震反射基本没有影响;地震子波频率为20～55Hz时,煤层使砂岩底面地震反射增强,但不会导致地震反射同相轴产生极性反转;当地震子波频率低于20Hz时,随着煤层距砂岩的位置发生变化,上覆煤层可能使砂岩底面地震反射减弱、增强或导致砂岩底面地震反射同相轴发生极性反转。当煤层远离砂岩,与砂岩之间的距离超过80m(双程时间厚度40.0ms)时,上覆煤层对砂岩底面地震反射不会产生影响。

4) 当上覆煤层厚度及位置发生变化时,砂岩顶、底面地震反射振幅不能反映砂岩厚度变化,不能利用砂岩顶、底面地震反射振幅预测薄层(d<λ/4)砂岩厚度。但当上覆煤层厚度及位置保持不变时,利用砂岩顶、底面地震反射最佳频率(最厚砂岩的调谐频率)的振幅信息可以预测薄层砂岩的厚度。

参 考 文 献

[1] Widess M B.How thin is a thin bed?[J].Geophysics,1973,38(6):1176-1180

[2] 凌云研究组.应用振幅的调谐作用探测地层厚度小于1/4波长地质目标[J].石油地球物理勘探,2003,38(3):268-274

Lingyun Group.Application of amplitude tuning in surveying geologic target thickness less than 1/4 wavelength[J].Oil Geophysical Prospecting,2003,38(3):268-274

[3] Kallweit R S,Wood L C.The limits of resolution of zero-phase wavelets[J].Geophysics,1982,47(7):1035-1046

[4] 黄文锋,姚逢昌,李宏宾.薄互层调谐规律研究与净厚度估算[J].石油地球物理探,2012,47(4):584-591

Huang W F,Yao F C,Li H B.Regularities of tuning effects of thin interbedded layers and their net thickness determination[J].Oil Geophysical Prospecting,2012,47(4):584-591

[5] 李国发,岳英,熊金良,等.基于三维模型的薄互层振幅属性实验研究[J].石油地球物理勘探,2011,46(1):115-120

Li G F,Yue Y,Xiong J L,et al.Experimental study on seismic amplitude attribute of their interbed based on 3D model[J].Oil Geophysical Prospecting,2011,46(1):115-120

[6] 李国发,岳英,国春香,等.基于模型的薄互层地震属性分析及其应用[J].石油物探,2011,50(2):144-149

Li G F,Yue Y,Guo C X,et al.Seismic attributes analysis based on model in interbedded layers and its application[J].Geophysical Prospecting for Petroleum,2011,50(2):144-149

[7] Sengbush R L,Lawrence P L,McDonald F J.Interpretation of synthetic seismograms[J].Geophysics,1961,26(2),138-157

[8] Wood L C.Imaging the subsurface[C]∥Jain K C,deFigueiredo R J P.Concepts and techniques in oil and gas exploration.Tulsa:Society of Exploration Geophysicists,1982:45-90

[9] Brown A R.Interpretation of three-dimensional seismic data[M].3rd ed.USA:American Association of Petroleum Geologists,1991:1-341

[10] Yilmaz O.Seismic data analysis[M].2nd ed.Tulsa:Society of Exploration Geophysicists,2001:1-1000

[11] 黄军斌,高利军,高勇,等.辫状河流相薄砂体地震子波效应和识别方法[J].石油与天然气地质,2010,31(2):225-231

Huang J B,Gao L J,Gao Y,et al.Wavelet effect and recognition methods of thin sand bodies in braided river facies[J].Oil & Gas Geology,2010,31(2):225-231

[12] Zeng H L,Backus M M.Interpretive advantages of 90°-phase wavelets,part I:modeling[J].Geophysics,2005,70(3),C7-C15

[13] 刘锐娥,李文厚,陈孟晋,等.鄂尔多斯东部下二叠统山西组2段储层评价及勘探前景[J].古地理学报,2006,8(4):531-538

Liu R E,Li W H,Chen M J,et al.Reservoir evaluation and exploration prospect of the Member 2 of Shanxi formation of lower permian in eastern Ordos[J].Journal of Palaeogeography,2006,8(4):531-538

[14] 王超勇,陈孟晋,汪泽成,等.鄂尔多斯盆地南部二叠系山西组及下石盒子组盒段沉积相[J].古地理学报,2007,9(4):369-378

Wang C Y,Chen M J,Wang Z C,et al.Sedimentary facies of the Shanxi formation and Member 8 of Xiashihezi formation of permian in southern Ordos basin[J].Journal of Palaeogeography,2007,9(4):369-378

[15] 叶黎明,齐天俊,彭海燕.鄂尔多斯盆地东部山西组海相沉积环境分析[J].沉积学报,2008,26(2):202-210

Ye L M,Qi T J,Peng H Y.Depositional environment analysis of Shanxi formation in eastern Ordos basin[J].Acta Sedmentologoica Sinica,2008,26(2):202-210

[16] Hatherly P.Overview on the application of geophysics in coal mining[J].International Journal of Coal Geology,2013,23(2):190-198

[17] Hongtao Z,Kaiyuan C,Keyu L,et al.A sequence stratigraphic model for reservoir sand-body distribution in the Lower Permian Shanxi Formation in the Ordos Basin,northern China[J].Marine and Petroleum Geology,2008,25(5):731-743

[18] Zeng H L,Backus M M,Barrow K T,et al.Stratal slicing:Part I,Realistic 3-D seismic model[J].Geophysics,1998,63(2):502-513

[19] Zeng H L,Henry S C,Riola J P.Stratal slicing:PartII,Realseismicdata[J].Geophysics,1998,63(2):514-522

[20] Zeng H L,Backus M M.Interpretive advantages of 90°-phase wavelets,part II:seismic applications[J].Geophysics,2005,70(3):C17-C24

[21] Zeng H L,Hentz T F,Wood L J.Stratal slicing of Miocene-Pliocene sediments in Vermilion Block 50-Tiger Shoal area,offshore Louisiana[J].The Leading Edge,2001,20(2):408-418

[22] Zeng H L,Hentz T F.High-frequency sequence stratigraphy from seismic sedimentology:applied to Miocene,Vermilion Block 50,Tiger Shoal area,offshore Louisiana[J].AAPG Bulletin,2004,88(2):153-174