基于各向异性岩石物理模型的页岩气储层横波速度预测

胡 起，陈小宏，李景叶

(1.中国石油大学(北京)油气资源与探测国家重点实验室，北京102249;2.中国石油大学(北京)CNPC物探重点实验室，北京102249)

地震勘探在非常规油气资源探测中扮演着不可替代的角色。随着地震勘探技术的不断创新与进步，叠前地震资料反演可以提供与地层岩性、物性以及含油气性有关的预测信息。横波速度在叠前地震资料反演以及AVO属性分析中具有非常重要的作用，联合纵波和横波信息有助于降低储层预测的不确定性，提高流体识别的精度。尽管如此，横波测井因其成本高，解释难度大等原因，在实际生产中仍较少被采用[1]。

基于岩石物理理论的方法是预测横波速度的主要手段，很多学者通过岩石物理测量，试图建立纵、横波速度间的经验关系，或者借助岩石物理模型由已知纵波速度和其它储层参数，如泥质含量、孔隙度等来估算横波速度。例如，Castagna等[2]给出了含水碎屑硅酸盐岩中纵波速度与横波速度的经验关系，包括著名的“泥岩线”公式;Han[3]在不同压力下测量了75块砂岩样品，得到了纵、横波速度间的线性回归方程;Nur等[4]提出了临界孔隙度模型，假设干岩石弹性模量与岩石孔隙度线性相关，进而预测横波速度;Xu等[5]结合Kuster-Toksoz模型[6]，微分等效介质理论和Gassmann方程[7]，建立了针对含泥砂岩的等效介质模型，也被称作Xu-White模型;Xu等[8]把Xu-White模型中的砂岩孔隙和泥岩孔隙替换为砂岩孔、泥岩孔、粒间孔和微裂缝四种类型，成功将该模型引入碳酸盐岩横波速度预测中。国内也有一些学者进行了横波预测的相关研究，李宏兵等[9]通过融合Gassmann方程和由微分等效介质理论建立的干岩石骨架模型——DEM解析模型，提出基于非线性模拟退火法反演岩石等效孔隙纵横比进行储层孔隙结构评价和横波速度预测的方法;刘欣欣等[10]提出基于自适应遗传算法反演岩石矿物组分的体积模量和剪切模量，进而确定碳酸盐岩储层岩性参数的方法。

然而，上述经验公式和理论模型均是针对常规碎屑岩和碳酸盐岩地层提出的，对页岩气储层并不适用。针对页岩气储层岩石物理建模及其横波速度预测的研究较少，最新进展来自Ruiz[11]，其采用各向同性自相容近似(self-consistent approximation,SCA)模型对Barnett页岩的两口井资料进行分析，预测出的纵波或横波速度与测井资料匹配较好。但页岩气藏因其各向异性程度高，对其采用各向同性近似并不合理，很可能带来不准确的预测结果。因此，通过建立一个适用性强的各向异性岩石物理模型来对页岩气储层进行横波预测有着较大的理论和实用价值。

基于各向异性微分等效介质(DEM)理论和Brown-Korringa各向异性流体替换模型，我们建立了有机页岩的各向异性岩石物理模型，提出了根据纵波速度反演岩石等效孔隙纵横比进行页岩气储层横波速度预测的方法。针对Bazhenov页岩样品实验室测量数据的应用试验结果表明，将岩石孔隙等效为具有单一孔隙纵横比的理想椭球孔，基于有机页岩各向异性岩石物理模型反演得到的等效孔隙纵横比能有效预测页岩气储层横波速度。

1 有机页岩岩石物理建模

我们针对有机页岩岩石物理建模的思路是:把有机页岩的基质看作是有机成分干酪根和非有机成分“粘土”矿物组成的两相混合物，通过各向异性DEM模型构建其等效弹性张量与孔隙度、流体饱和度及孔隙纵横比的关系式;将岩石孔隙等效为具有单一纵横比的椭球体，采用各向异性DEM模型将干燥的孔隙包含物加入到有机页岩基质中，得到孔隙介质干岩石的等效弹性张量关系式;采用Brown-Korringa各向异性流体替换理论，由干岩石等效弹性张量得到流体饱和岩石等效弹性张量，从而建立起有机页岩各向异性岩石物理模型。

1.1 干酪根—粘土混合物等效弹性张量的计算

微分等效介质理论可用来模拟双相混合物，其首先假设有一体积为V0的固体矿物相作为岩石基质，往其中加入体积为ΔV的包含物相，并替换掉相同体积(ΔV)的矿物相，用新产生的复合材料的等效弹性模量形成的均匀介质代替原来的岩石基质，重复上述过程，直到满足固体矿物相与包含物相的体积比率[12-13]。Hornby[14]给出了各向异性DEM的表达式：

(1)

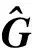
DEM方法的两个准则是：①如果某一相是连续的，采用DEM模型往其中加入另一相后依然能保证它是连续的;②如果某一相是不存在的，或存在但不连续，通过DEM模型得到的等效介质中其依然是不连续的。因此，DEM模型模拟的岩石内部结构是包含物相离散分布在连续的矿物初始相中。将相1看作初始相逐渐加入相2，与将相2看作初始相逐渐加入相1至同等比例，所得等效介质性质是不同的[12]。同样，对有机页岩而言，将其看作VTI介质时，不同的干酪根分布形式会带来不同的DEM模型计算结果(图1和图2)。在很多富含有机质页岩中，扫描电子显微镜(SEM)显示出斑块状的干酪根颗粒离散分布在由非有机物形成的岩石基质中[15-17];对于其它页岩，也有学者通过SEM分析认为应将干酪根看作岩石基质而非离散分布的包含物[18-19]。因此，确定干酪根的分布形式应借助于实际岩样的电学观测资料。

图1和图2显示了两种不同的干酪根分布形式下干酪根—粘土两相混合物的等效刚度系数C11，C33，C44和C66随干酪根含量的变化趋势，其中C11和C33分别表示介质在平行层面和垂直层面方向的抗压缩能力；C44和C66分别表示介质在平行层面和垂直层面方向的抗剪切能力。图1是干酪根颗粒作为椭球形包含物离散分布在连续的粘土基质中;图2是粘土颗粒作为椭球形包含物离散分布在连续的干酪根基质中。其中包含物的纵横比α依次取为0.1，0.2，0.5和1.0。模型中假设干酪根和粘土矿物均为各向同性的，它们的体积模量K和剪切模量G分别为：干酪根K=2.9GPa,G=2.7GPa[12];粘土K=22.9GPa，G=10.6GPa[14]。

从图1和图2中可以看出，尽管模型的输入两相都是各向同性的，非球形的包含物形状使得等效介质表现出各向异性特征。干酪根含量一定时，包含物变“瘦”会使平行层面方向的刚度系数C11和C66增大，垂直层面方向的刚度系数C33和C44减小。当包含物纵横比为1时，C11与C33，C44与C66两条曲线彼此重合(图1和图2中曲线簇中间的一根紫红色曲线),等效介质表现出各向同性。

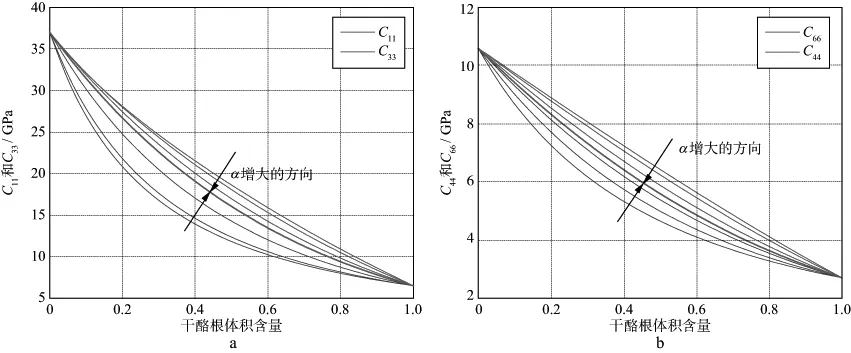
图1 干酪根作为包含物时，干酪根—粘土两相混合物纵波等效刚度系数(a)和横波等效刚度系数(b)随干酪根含量的变化特征(箭头指向包含物纵横比α增大的方向)

图2 干酪根作为岩石基质时，干酪根—粘土两相混合物纵波等效刚度系数(a)和横波等效刚度系数(b)随干酪根含量的变化特征(箭头指向包含物纵横比α增大的方向)

图3 干酪根分别作为包含物(情形Ⅰ)和作为岩石基质(情形Ⅱ)，α=0.1时干酪根—粘土两相混合物的纵波等效刚度系数(a)和横波等效刚度系数(b)

另外，当模型两相的体积含量以及包含物的纵横比一定时，将干酪根看作包含物时求得的各刚度系数都要大于干酪根作为岩石基质时的情形，即模拟得到的等效介质更坚硬(见图3，以α=0.1为例)。图3给出了干酪根分别作为包含物(情形Ⅰ，图中实线)和作为岩石基质(情形Ⅱ，图中虚线)时，在α=0.1时干酪根—粘土两相混合物的纵波等效刚度系数(图3a)和横波等效刚度系数(图3b)。

1.2 干岩石等效弹性张量的计算

考虑干酪根作为岩石基质时的情形。同样，我们采用各向异性DEM模型往干酪根—粘土混合物中加入单一纵横比的空孔隙包含物，模型中的初始相取干酪根含量为20%时干酪根与粘土的混合物，粘土矿物纵横比同样依次取值0.1，0.2，0.5和1.0，得到干岩石的等效刚度张量随孔隙度的变化特征如图4所示。

由图4可以看到，等效干岩石的硬度会随着孔隙度的增大而降低，孔隙纵横比对干岩石刚度系数的影响同上节所述包含物纵横比对两相混合物弹性性质的影响一样;不同的是，由于模型初始相是各向异性的，即使孔隙纵横比为1时，干岩石依然表现出各向异性特征。

图4 干岩石纵波等效刚度系数(a)和横波等效刚度系数(b)随孔隙度变化特征

1.3 流体饱和岩石等效弹性张量的计算

Brown-Korringa模型[20]描述了各向异性干岩石的有效弹性张量与流体饱和岩石的有效弹性张量之间的关系，通常被视为各向异性Gassmann模型：

(2)

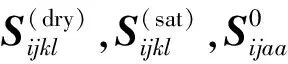
我们采用Brown-Korringa模型计算盐水饱和情况下有机页岩的等效弹性张量，模型中干岩石的弹性性质取孔隙纵横比为0.1时的情形，盐水弹性模量为K=2.2GPa和G=0，计算结果如图5所示。从图5中可以看到，流体(盐水)的加入会增大干岩石的纵波刚度系数C11和C33(图5a)，但对横波刚度系数C44和C66没有影响(图5b)。

图5 流体(盐水)对干岩石纵波刚度系数(a)和横波刚度系数(b)的影响

1.4 有机页岩各向异性岩石物理建模流程

我们建立了有机页岩各向异性岩石物理建模流程(图6)。

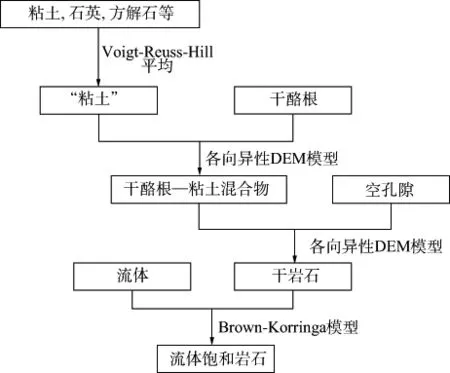
图6 有机页岩各向异性岩石物理建模流程

2 横波速度预测原理

基于上述建立的各向异性岩石物理模型，根据各向异性介质纵、横波速度与其刚度系数的关系式，将流体饱和岩石的等效弹性张量转化为速度;由岩石的纵波(或横波)速度可以反演出等效孔隙纵横比;将反演得到的等效孔隙纵横比再代入到流体饱和岩石的等效刚度张量计算式中，便可预测出有机页岩的横波(或纵波)速度。

Thomsen(1986)给出了横向各向同性介质中沿对称轴方向的纵、横波速度与其刚度张量之间的关系：

其中：C33和C44分别表示介质沿对称轴方向的纵波和横波刚度系数;ρ是密度。

(1)式和(2)式表明，流体饱和岩石的弹性张量不仅是矿物颗粒的弹性张量和孔隙度的函数，而且与岩石的孔隙纵横比密切相关。把(1)式和(2)式代入(3)式和(4)式中，我们就建立了纵、横波速度与孔隙纵横比之间的非线性关系式。利用这样的关系式，我们既可以根据岩石基质矿物组分的弹性张量，以及孔隙度、流体饱和度和孔隙纵横比，正演得到岩石的纵、横波速度;也可以根据岩石的纵波(或横波)速度来反演等效孔隙纵横比。

为了利用纵波速度来反演岩石孔隙的纵横比，进而预测横波速度，这里我们把岩石的孔隙简单等效为具有单一纵横比的理想椭球孔，反演中采用的目标函数为

(5)

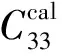
3 岩样数据应用试验

Vernic等[18]通过X射线衍射法(XRD)给出了Bazhenov页岩8块岩样的平均矿物含量。这些样品都取自西西伯利亚盆地东北部的一口井中，取样深度在3784～3842m。文献[18]中进一步提供了这8块岩样在干燥情况下和其中5块岩样在流体饱和情况下的超声波速度。表1显示了目标页岩除干酪根以外的4种主要矿物成分以及它们的相对体积含量。其中粘土的弹性模量K和G取自Hornby[14];其他矿物的弹性模量K和G取自Mavko[12]。我们将表1中4种矿物的混合物称为“粘土”矿物，利用Voigt-Reuss-Hill平均可求得此“粘土”矿物的弹性模量为：K=32.08GPa，G=23.92GPa。

为了解Bazhenov页岩的内部结构，文献[18]中给出了使用光学显微镜和扫描电镜(SEM)的分析结果。光学显微照片(图7)显示，白色的“粘土”矿物和黑色的干酪根颗粒水平定向排列程度较强，页理构造明显，岩石可等效为具有垂直对称轴的横向各向同性介质。而扫描电镜图片显示，富含有机质页岩中的干酪根将“粘土”矿物彼此分离开来，干酪根在岩石中形成一个连续的背景骨架，被分离开来的非有机成分呈透镜体形状排列。

图7 Bazhenov页岩(3824m处岩心)的光学显微照片(白色部分是“粘土”矿物，黑色部分为干酪根)

因此，利用(1)式计算粘土—干酪根两相混合物的弹性性质时，我们将干酪根看作岩石基质，然后逐渐加入“粘土”矿物包含物至相应含量，得到“粘土”矿物离散分布在连续的干酪根背景基质时两相混合物的等效刚度张量。接着继续使用各向异性DEM模型将孔隙包含物加入两相混合物中，得到干岩石的等效刚度张量并代入(3)式和(4)式中，可求出干岩石垂直层面方向的纵波和横波速度。利用(2)式可计算出饱含水时岩石的等效刚度张量，进而求出饱含水时岩石的纵波和横波速度。在计算过程中，对某一深度处岩样，将其等效孔隙纵横比看作唯一的变量，预测出的纵波和横波速度是孔隙纵横比的函数。采用以上第2章所述的横波速度预测原理，通过拟合预测纵波速度和实测纵波速度，反演出各个深度最佳的等效孔隙纵横比，进而求出相应的横波速度。

实际页岩中由于孔隙流体与岩石骨架发生化学作用，可使岩石膨胀软化。当页岩中存在蒙脱石矿物时，软化作用尤其强烈，容易模糊流体对干岩石刚度的增强作用。Vernik等[21]对不含蒙脱石的Bakken页岩3428m处岩心和蒙脱石含量为6%的Bazhenov页岩3488m处岩心进行了对比分析，发现在70MPa围压下，往干岩石中注入盐水后，两者的纵波速度仅增大了1%左右，并且前者的横波速度几乎不变，但后者的横波速度减小10%。由于两处岩心的孔隙度均小于5%，盐水对其产生的硬化作用很小，可见，蒙脱石带来的化学软化作用主要是影响横波速度。因此，在利用有机页岩岩石物理模型对Bazhenov页岩的流体饱和岩样进行横波速度预测之前，我们采用10%这一比例对各岩样横波速度进行了补偿。

图8为Bazhenov页岩8组干燥岩样和其中5组盐水饱和岩样的纵波速度拟合情况以及预测横波速度与实测横波速度的对比(粘土包含物纵横比仍取0.1)。从图8中可以看出，在预测纵波速度与实测纵波速度几乎重合的情况下，预测横波速度与实测横波速度吻合较好，平均相对误差仅为0.0023，说明本文方法可有效预测有机页岩的横波速度。另外，流体饱和岩样普遍比干燥岩样的横波速度预测误差大，这可能与我们采用相同比例系数对蒙脱石的软化作用进行补偿有关。当岩石中不含蒙脱石矿物，或孔隙流体与岩石骨架之间的化学作用可忽略不计时，该方法可能具有更高的预测精度。

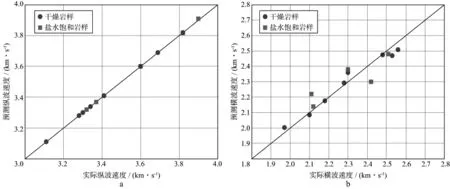
图8 Bazhenov页岩的纵波速度拟合情况(a)和横波速度预测效果(b)

4 结论与讨论

本文基于各向异性微分等效介质理论(DEM)和Brown-Korringa各向异性流体替换模型，建立了有机页岩各向异性岩石物理模型，提出一种基于单孔隙纵横比模型的有机页岩横波速度预测方法。通过各向异性DEM模型计算有机成分干酪根和非有机成分“粘土”矿物组成的两相混合物的等效弹性张量;将岩石孔隙等效为具有单一纵横比的椭球体，采用各向异性DEM模型将干燥的孔隙包含物加入岩石基质中，得到干岩石的等效弹性张量;采用Brown-Korringa各向异性流体替换模型，由干岩石等效弹性张量得到流体饱和岩石等效弹性张量，从而建立起有机页岩各向异性岩石物理模型。根据各向异性介质纵、横波速度与其刚度系数的关系式，将流体饱和岩石的等效弹性张量转化为速度;拟合模型预测的纵波速度与实测纵波速度，反演出各个深度最佳的等效孔隙纵横比;将反演结果代入到有机页岩岩石物理模型中，即可有效进行横波速度预测。

需要指出的是，本文应用试验中在利用Voigt-Reuss-Hill模型计算粘土矿物的等效弹性模量时，采用的是Bazhenov页岩8组岩样的平均矿物含量，这会影响到横波预测结果的精度，更精确的预测结果有赖于借助实验室X射线衍射(XRD)的方法来分析各个岩样的矿物组分。另外，本文将岩石孔隙等效为具有单一纵横比的理想椭球孔，比较适合于实际储层类型为单一的孔隙型或裂缝型储层。当然，对于多重孔隙类型的复杂储层，依然可以利用本文的方法反演得到一个等效的孔隙纵横比用于横波预测。至于如何从声波数据中反演出多重孔隙各自的纵横比进行储层孔隙评价将是下一步有待研究解决的问题。

参 考 文 献

[1] 孙福利,杨长春,麻三怀，等.横波速度预测方法[J].地球物理学进展,2008,23(2):470-474

Sun F L,Yang C C,Ma S H,et al.An S-wave velocity predicted method[J].Progress in Geophysics,2008,23(2):470-474

[2] Castagna J P,Batzle M L,Eastwood R L.Relationships between compressional-wave and shear-wave velocities in clastic silicate rocks[J].Geophysics,1985,50(4):571-581

[3] Han D H,Nur A,Morgan D.Effects of porosity and clay content on wave velocities in sandstones[J].Geophysics,1986,51(11):2093-2107

[4] Nur A,Mavko G,Dvorkin J,et al.Critical porosity:a key to relating physical properties to porosity in rocks[J].The Leading Edge,1998,17(3):357-362

[5] Xu S,White R E.A new velocity model for clay-sand mixtures[J].Geophysical Prospecting,1995,43(1):91-118

[6] Kuster G T,Toksöz M N.Velocity and attenuation of seismic waves in two-phase media[J].Geophysics,1974,39(5):587-618

[7] Gassmann F.Über die elastizität poröser medien[J].Vier der Natur Gesellschaft in Zürich,1951,96:1-23

[8] Xu S,Payne M A.Modeling elastic properties in carbonate rocks[J].The Leading Edge,2009,28(1)：66-74

[9] 李宏兵,张佳佳,姚逢昌.岩石的等效孔隙纵横比反演及其应用[J].地球物理学报,2013,56(2):608-615

Li H B,Zhang J J,Yao F C.Inversion of effective pore aspect ratios for porous rocks and its applications[J].Chinese Journal of Geophysics,2013,56(2):608-615

[10] 刘欣欣,印光耀,张峰.一种碳酸盐岩储层横波速度估算方法[J].中国石油大学学报(自然科学版),2013,37(1):42-49

Liu X X,Yin G Y,Zhang F.S-wave velocity estimation method in carbonate reservoir[J].Journal of China University of Petroleum,2013,37(1):42-49

[11] Ruiz F,Azizov I.Tight shale elastic properties using the soft-porosity and single aspect ratio models[J].Expanded Abstracts of 81stAnnual International SEG Meeting,2011,2241-2245

[12] Mavko G,Mukerji T,Dvorkin J.The rock physics handbook[M].London:Cambridge University Press,2009,1-522

[13] Ruiz F，Dvorkin J.Predicting elasticity in nonclastic rocks with a differential effective medium DEM model[J].Geophysics,2010,75(1):E41-E53

[14] Hornby B E,Schwartz L M,Hudson J A.Anisotropic effective-medium modeling of the elastic properties of shales[J].Geophysics,1994,59(10):1570-1583

[15] Loucks R G,Reed R M,Ruppel S C,et al.Morphology,genesis,and distribution of nanometer scale pores in siliceous mudstones of the mississipian Barnett Shale[J].Journal of Sedimentary Research,2009,79(12):848-861

[16] Curtis M E,Sondergeld C H,Ambrose R J,et al.Microstructural investigation of gas shales in two and three dimensions using nanometer-scale resolution imaging[J].AAPG Bulletin,2012,96(4):665-677

[17] Sondergeld C H,Rai C S.Elastic anisotropy of shales[J].The Leading Edge,2011,30(3),234-331

[18] Vernik L,Landis C.Elastic anisotropy of source rocks:implications for hydrocarbon generation and primary migration[J].AAPG Bulletin,1996,80(4):531-544

[19] Bayuk I O,Ammerman M,Chesnokov E M.Upscaling of elastic properties of anisotropic sedimentary rocks[J].Geophysical Journal International,2008,172(2):842-860

[20] Brown R,Korringa J.On the dependence of the elastic properties of a porous rock on the compressibility of the pore fluids[J].Geophysics,1975,40(4):608-616

[21] Vernik L,Liu X.Velocity anisotropy in shales:a petrophysical study[J].Geophysics,1997,62(2):521-532