页岩干酪根吸附规律的分子模拟研究

2022-06-23李晶辉黄思婧余洋阳强贤宇顾康福侯大力2

油气藏评价与开发 2022年3期

李晶辉，韩鑫，黄思婧，余洋阳，强贤宇，顾康福，侯大力2,

（1.中国石化西北油田分公司石油工程技术研究院，新疆乌鲁木齐 830011；2.成都理工大学油气藏地质及开发工程国家重点实验室，四川成都 610059；3.成都理工大学能源学院，四川成都 610059）

页岩气是指赋存于富有机质页岩的非常规天然气[1-3]，其中吸附气占比介于20 %～85 %[4]。页岩气后期稳产主要依赖于吸附气解吸，但目前我国页岩气吸附特征和机理仍然缺乏研究，因为吸附气主要赋存于页岩气干酪根内部的微纳米孔隙中，实验室无法模拟页岩气藏低孔低渗、高温高压的环境，无法对页岩气微观的吸附机理进行研究。而通过分子模拟的方法，可以从微观角度研究页岩气在干酪根中的吸附机理，分析压力、温度和孔径对页岩气吸附行为的影响。目前已有国内外学者使用分子模拟技术研究CH4在干酪根表面的吸附[5-7]。

AMBROSE 等[8]发现页岩孔隙体积与自由气体体积不是相同的，并认为页岩气吸附符合Langmuir 理论（单分子吸附理论）。刘冰等[9]以石墨狭缝结构代替页岩孔隙，研究CH4气体在页岩孔隙中的吸附现象，分析了不同尺寸的狭缝和不同温度下CH4的密度分布，但温度对吸附影响的原因并未做出解释，对于吸附量只是用密度进行表征，并没有定量表示。陈磊等[10]在研究温度变化的基础上，新增研究压力变化及孔径表面的水对CH4吸附的影响，发现狭缝表面有水会减弱吸附效果，但是文章也并没有对吸附量进行定量表示，只是以密度来描述吸附强弱。田守嶒等[11]认为页岩干酪根并不能简单地用石墨来表征，根据干酪根的元素含量、分子结构建立了复杂的干酪根分子模型，并研究了温度、地温梯度、干酪根分子组成、比表面积对页岩吸附CH4的影响。卢双舫等[12]发现分子模拟得到的超额吸附量比实验得到的吸附量高出一个数量级，因为影响吸附能力的是表面积不是体积，将吸附量单位转变为表面积单位，发现实验与分子模拟结果拟合程度较好。唐鑫等[13]通过实验发现页岩中孔容比和比表面积的主要由2 nm以下的孔径贡献；通过模拟得出CH4吸附伊利石符合Langmuir 吸附理论模型。XIONG 等[14]通过实验和分子模拟发现干酪根对CH4的吸附能力大于矿物，即CH4的吸附能力下降依次为：有机孔隙，黏土矿物，石英孔隙，并发现比表面积是影响CH4吸附能力的主要因素。HAMZA 等[15]通过实验测试了页岩对天然气中不同组分的吸附优先性。发现氮气驱是一种不成功的气体提高采收率技术，这是因为CH4的优先吸附性在N2之上，所以很难置换CH4；而CO2的吸附能力在CH4之上，这也说明CO2可以提高页岩气的采收率。KATTI 等[16]构建了比较复杂且完整的三维干酪根模型，该分子模型由7 个二维结构组成。许晨曦等[17]通过分子模拟发现不同矿物其吸附能力：干酪根大于黏土矿物、大于石英，原因是气体在矿物表面吸附位特征（吸附质密度和吸附强度）的不同。

结合近几年国内外研究发现：在石油领域分子模拟技术处于初步发展阶段，但分子模拟从微观角度分析吸附，具有宏观无法替代的技术优势。利用真实的Ⅱ型干酪根分子建立干酪根狭缝模型，比起石墨模型更加接近页岩真实构造；采用分子动力学模拟方法，探索吸附规律和机理；并对真实干酪根模型进行全面敏感性分析，包括孔径大小、温度、压力对CH4吸附的影响；通过径向分布函数和吸附热的规律，探究甲烷在干酪根上吸附的原因。

1 模拟方法

1.1 模型建立

页岩中有机质成分主要为干酪根，其成分复杂，怎么样准确地描述分子尺度上的干酪根仍然是目前的热点问题。干酪根类型可以分为3类：Ⅰ型为腐泥型干酪根，来自藻类物质的聚集；Ⅱ型为混合型干酪根，来源于浮游生物；Ⅲ型为腐殖型干酪根，来源以陆地高等植物为主。中国四川龙马溪组海相页岩是目前页岩气开发的主力军，龙马溪组页岩TOC（总有机碳含量）介于2.0～4.0 ，页岩干酪根类型主要为Ⅰ-Ⅱ型，以Ⅱ型为主，和美国Barnett 页岩干酪根一样[18]。研究将构建Ⅱ型干酪根分子模型，并用Barnett 页岩进行验证。UNGERER 等[19]通过实验数据构建了真实的干酪根分子，如图1 所示，分子式为C252H294O24N6S3，具体的模型参数见表1。选取16 个干酪根分子构建密度为1.0 g/cm3的Ⅱ型干酪根骨架结构，结构构型见图2 和图3。图2 中孔径H为构成孔径上下两层干酪根表面的距离；图3中Lx与Ly为模拟盒子的x和y方向的长度，其中Lx为4.011 nm，Ly为4.011 nm。CH4分子模型见图4，其键长为0.109 1 nm，键角为109.470°。

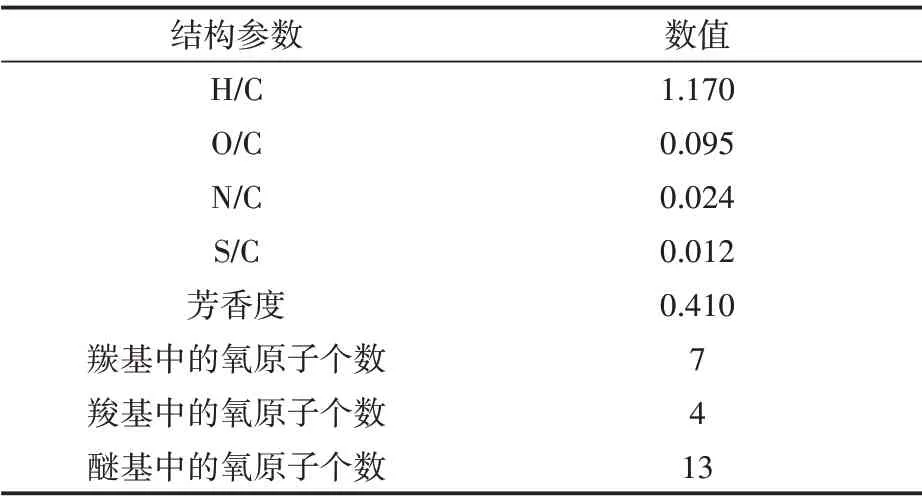
表1 干酪根模型参数Table 1 Physical characteristics of kerogen

图1 Ⅱ型干酪根分子模型Fig.1 Molecular model of type Ⅱkerogen

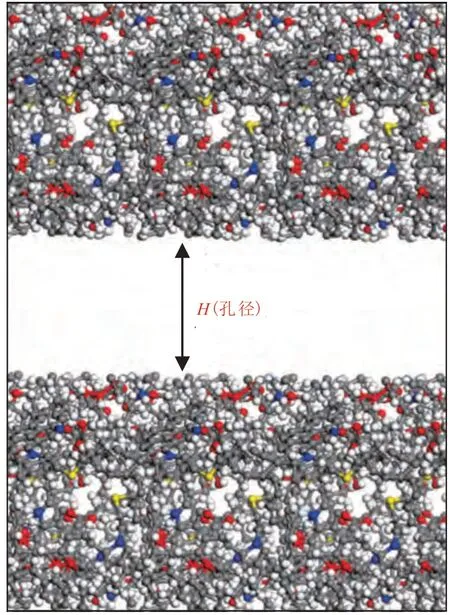
图2 Ⅱ型干酪根模型孔径结构构型Fig.2 Pore size configuration of type Ⅱkerogen model

图3 Ⅱ型干酪根模型x×y方向截面Fig.3 Cross section of kerogen model in direction of x×y

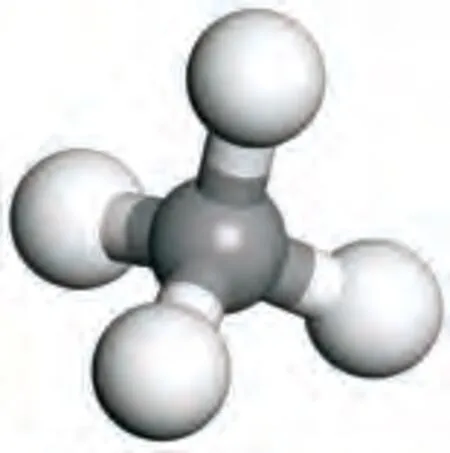
图4 CH4分子模型Fig.4 Molecular model of CH4

1.2 势能模型与参数

构建的页岩干酪根模型，CH4分子均保持电中性，可采用L-J 势函数进行表征，表2 为模拟中出现的L-J 势能参数。模拟中假定干酪根和CH4为刚性体，由于CH4分子的原子不带电荷，与干酪根的相互作用不需要考虑库仑力，只需要考虑短程范德华力的相互作用[5]。L-J势函数的描述如下：

表2 模拟中出现的L-J势能参数Table 2 L-J potential parameters in simulation

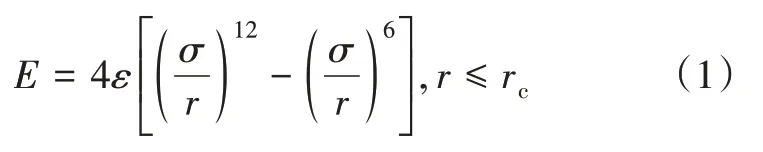
式中：E为两个原子或两个分子间的相互作用能，kcal/mol；ε为势井深度，kcal/mol；σ为相互作用的势能等于0 时原子间的距离，nm；r为原子间的距离，nm；rc为截断距离，nm。

1.3 模拟条件

主要研究不同温度、不同压力、不同孔径的影响因素对CH4在干酪根中吸附能力的影响。其中，模拟的温度设置5 个模拟点，温度介于298 ～378 K；模拟的压力设置6 个模拟点，压力介于5～30 MPa；模拟的孔径设置分别为1，2，3，4，5，10，15，20 nm。

主要采用蒙特卡洛方法和分子模拟方法研究CH4在干酪根中的吸附行为。利用Materials Studio（美国Accelrys 公司开发的分子模拟软件）的Sorption吸附版块完成CH4在干酪根中的吸附模拟任务，模拟中使用正则系综，模拟体系采用周期性边界条件，为使体系逸度达到平衡，对体系进行1×105步的平衡模拟，之后对体系进行1×106步的过程模拟，结果数据主要收集后1×106步。模拟过程中干酪根分子固定不动。

分子模拟的实验条件都超过了CH4的临界条件（T=190.55 K，p=4.59 MPa），CH4处于超临界状态[20]。在超临界状态下，绝对吸附量和超额吸附量结果会出现明显的差距。因此，有必要将绝对吸附量转化为超额吸附量。根据前人得到的结论[21-22]，转化公式如下：

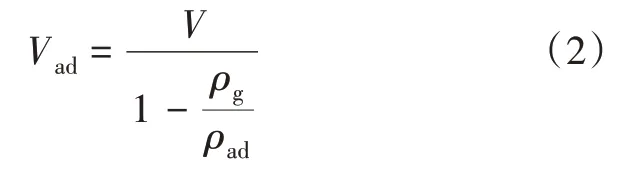
式中：Vad为绝对吸附量，mmol/m2；V为超额吸附量，mmol/m2；ρg为气相密度，g/cm3；ρad为吸附相密度，g/cm3。

1.4 模型验证

首先将模拟结果与CH4在干酪根中吸附的实验结果[23]进行对比，图5 为模拟结果（T=338 K）和Barnett 页岩（T=338 K）对比图，Barnett 页岩干酪根以Ⅱ型干酪根为主，可以发现模拟结果与实验结果有一定误差，误差控制在10 %以内。这是由于实际模型孔隙复杂，与模拟的干酪根模型有一定差别。

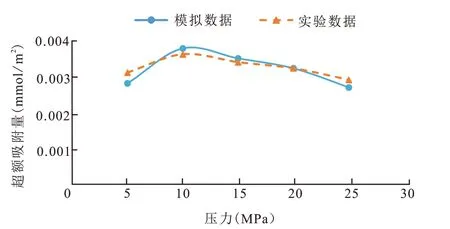
图5 模拟值与实验值的超额吸附量对比（T=338 K）Fig.5 Comparison of excess adsorption capacity between simulated and experimental values（T=338 K）

2 模拟结果

2.1 不同孔径、压力对CH4在干酪根中吸附的影响

图6 为不同孔径下CH4分子在干酪根狭缝孔吸附的微观结构。可以发现随着孔径的增加，吸附在干酪根壁面的CH4分子有明显增多，这是由于来自干酪根的吸引力大于来自甲烷整体的吸引力，形成势陷，导致界面附近CH4密度高于体相CH4密度。而且从截面图明显看出孔径小于1 nm 时，孔隙中没有游离态CH4分子；当孔径大于1 nm 时，孔径中存在了少量的游离态CH4分子，说明在不同孔径中CH4分子的赋存状态存在差异。图7 为不同孔径下CH4吸附干酪根的绝对吸附量和超额吸附量曲线图，可以发现：绝对吸附量随着压力的升高而增大；而超额吸附量在压力升高到某个值后，达到一个最大值，最大压力分布在10 MPa左右，随着压力的继续升高，吸附量呈现下降趋势。这是因为随着压力的升高，CH4的体相密度变大，使得CH4体相对界面附近的甲烷吸引力增加，反而使得干酪根对界面附近的CH4吸附作用减弱，即压力在10 MPa之上时，吸附量反而减少。

图6 不同孔径下CH4分子在干酪根狭缝孔吸附的微观结构Fig.6 Microstructure of adsorption of CH4 in kerogen slit pores at different pore sizes

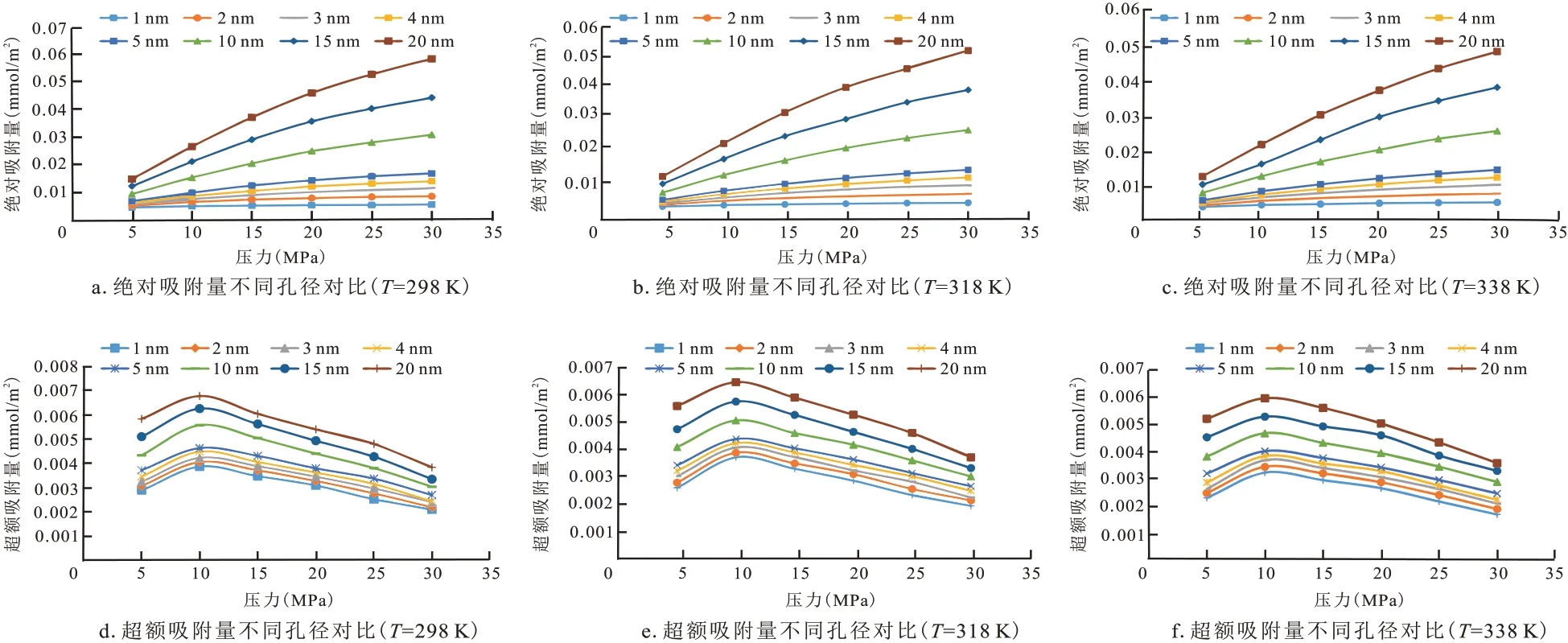
图7 不同孔径下的绝对吸附量和超额吸附量对比曲线Fig.7 Comparison curves of absolute and excess adsorption capacity at different pore sizes

2.2 不同温度、压力对CH4在干酪根中吸附的影响

图8 为不同温度下的绝对吸附量和超额吸附量的曲线图。以1 nm 为例，不同温度的超额吸附量最大值所在的最大压力均为10 MPa 左右，并且随着温度的升高而降低，其温度为298，338，378 K 的超额吸附量的最大值分别为0.004 351，0.003 813，0.003 295 mmol/m2；CH4的绝对吸附量随着压力的增加均呈现出了上升趋势变缓慢的现象，并且也随着温度的升高而下降。以上结果说明在压力一定的情况下，温度越高越不利于干酪根吸附CH4分子，这是由于高温时分子热运动增强，动能增大，导致CH4分子在干酪根表面吸附概率降低，吸附量减小。

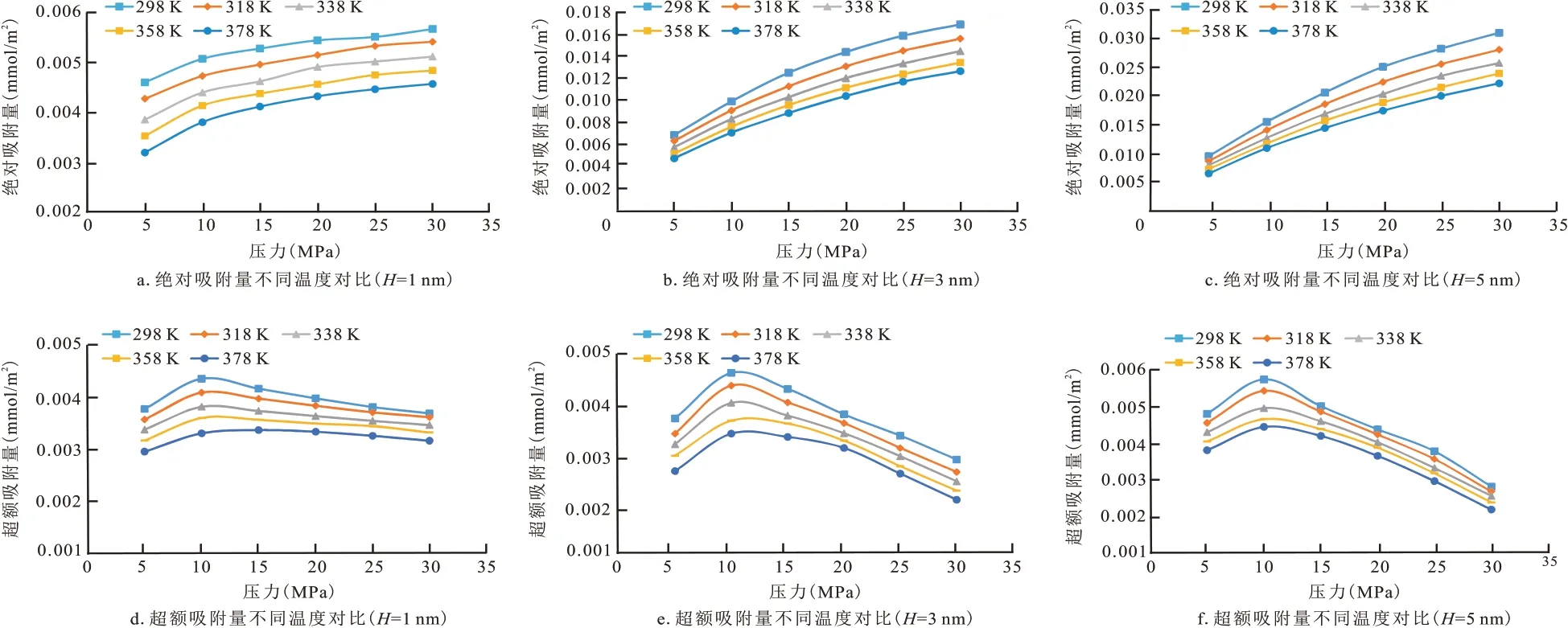
图8 不同温度下的绝对吸附量和超额吸附量对比曲线Fig.8 Graphs of absolute and excess adsorption at different temperatures

2.3 径向分布函数

为了研究干酪根各元素对CH4吸附影响的大小，利用径向分布函数分析CH4中C 原子与干酪根中C、O、N、S 的相关性。径向分布函数是两个原子互相占据空间的概率[24]。图9 为CH4与干酪根各原子间的径向分布函数。CH4与干酪根中的C 原子的函数峰值大于CH4与O、N 和S 原子的函数峰值，这是由于C原子容易形成电负性，相较O、N 和S 原子而言，CH4分子与干酪根中的C 原子有较强的相互作用。图9中CH4分子与干酪根各原子间的径向分布函数的规律可适用于所有干酪根类型。

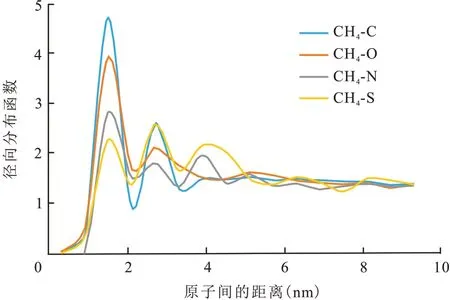
图9 CH4与干酪根各原子间的径向分布函数Fig.9 Radial distribution functions between atoms of CH4 and kerogen

2.4 吸附热

图10 是不同孔径中CH4在干酪根吸附的等量吸附热，随着孔径H的增加，CH4的等量吸附热逐渐下降，并且下降趋势趋于平缓。当孔径为1 nm时，干酪根的CH4平均等量吸附热为22.61 kJ/mol；当孔径为20 nm时，干酪根的CH4平均等量吸附热为7.74 kJ/mol。可以发现干酪根的CH4平均等量吸附热均小于40 kJ/mol，物理吸附的吸附热是吸附质的凝缩热与湿润热之和，最大不会超过40 kJ/mol，说明CH4在页岩干酪根上的吸附属于物理吸附。

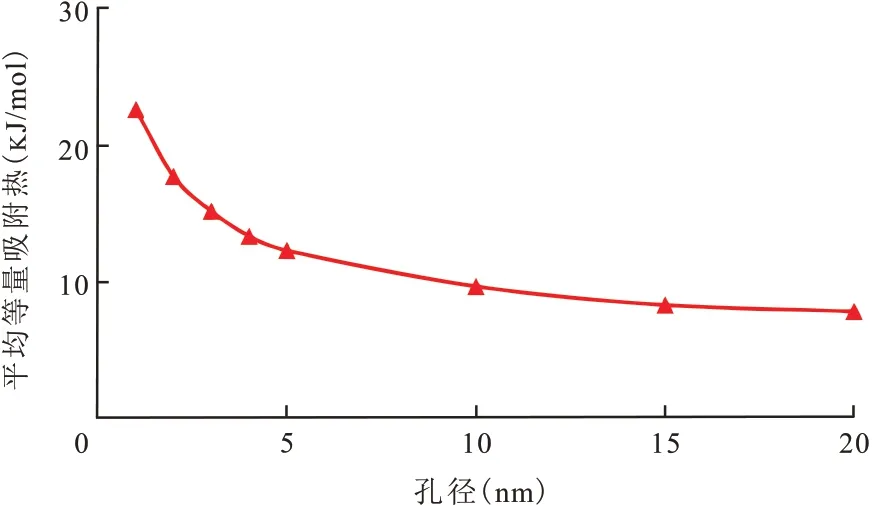
图10 CH4在干酪根不同孔径中的平均等量吸附热Fig.10 Average heat of adsorption of CH4 in kerogen with different pore sizes

2.5 密度分布

图11 为不同孔径中压力为20 MPa 的局部密度（T=338 K），局部密度按照狭缝孔显示方向进行统计，可以发现在不同孔径的干酪根孔隙中，在干酪根孔隙两侧壁面有明显的CH4分子聚集，并呈现轴对称现象，这与两侧干酪根原子的排列对称有关。在不同孔径的干酪根中，在靠近两侧孔壁面的位置出现明显的密度峰值，并且孔径在1 nm 时，只有1 个密度峰值。随着孔径的增加，曲线密度峰值也逐渐增多，这表明1 nm 时孔隙中只存在吸附气。当孔径大于1 nm 时，干酪根孔中出现游离气，随着孔径的增加，孔隙中将同时共存游离气和吸附气。

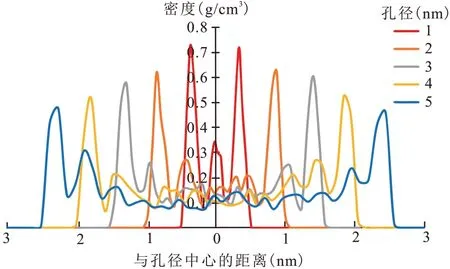
图11 CH4在干酪根不同孔径中的密度分布（T=338 K，p=20 MPa）Fig.11 Density distribution of CH4 in kerogen with different pore sizes（T=338 K,p=20 MPa）

3 讨论

通过分子模拟研究页岩吸附可以弥补实验在微观研究的不足，其不仅可以实现对实验温度、压力范围的扩展，还能够基于原子细节揭示受限空间页岩气的动力学行为及其与干酪根表面的微观相互作用机理。页岩吸附气的动用程度与压力有密切关联，通过最大超额吸附量来确定临界解吸压力，可用于评价页岩吸附气的动用程度，能为提高页岩气的采收率提供更加准确的借鉴和帮助。