奇异值谱分析在绕射波分离及成像中的应用
2014-03-25刘太臣胡江涛王华忠王西文刘文卿
刘太臣,胡江涛,王华忠,王西文,刘文卿
(1.同济大学海洋与地球科学学院波现象与反演成像研究组,上海200092;2.中国石油天然气股份有限公司勘探开发研究院西北分院,甘肃兰州730020)
地层中存在有很多小尺度的地质构造,如断层、裂隙(缝)、孔洞等,它们的地震响应为地震记录中弱能量的绕射波[1]。这些小尺度的地质目标体是常见的油气运移通道和储集体,使得弱能量的绕射波成像具有较高的研究和实用价值。这些地震异常体在常规流程处理的成像结果中会被强能量的反射体所掩盖。为了在地震成像剖面上有效识别这些小尺度异常体,可进行反射波场和绕射波场的分离,然后对绕射波场进行成像,以实现加强绕射体的目标成像。
反射波和绕射波的分离是基于二者在动力学和运动学两方面的特征差异[2],传统的分离方法主要基于二者的运动学特征差异。在20世纪80年代,人们就提出利用绕射波时距曲线构建绕射时间剖面(D-Section)的方法来实现绕射波叠加,从而分离绕射波场和反射波场[2-3]。近年来,Khaidukov等[4]提出利用反射波时距曲线,将反射波聚焦于其成像点上,然后去掉聚焦的反射波场来得到绕射波场;Taner等[5]和孔雪等[6]在平面波域利用平面波滤波[7]实现线性特征的反射波和双曲特征的绕射波分离;Reshef等[8]和Landa等[9]提出在Dip-angle成像道集中利用平面波滤波分离绕射波和反射波,二者在成像域Dip-angle道集上的不同特征为:偏移速度正确的情况下,地下层状反射界面产生的反射波为双曲特征,而散射点产生的绕射波为线性特征;由于反射波和绕射波旅行时场的计算参数不同,时间偏移中的CRS技术[10]和多聚焦技术[11]也被应用到绕射波的分离与成像中。
我们首先分析反射波和绕射波的运动学和动力学特征差异,然后同时利用这两种差异,采用f-x域奇异值谱分析(SSA)方法,压制共偏移距道集中具有强能量和线性特征的反射波场,以达到突出并分离绕射波场的目的,进而实现绕射体的目标成像,使得小尺度异常体在成像结果中更易于识别。模型数据和实际数据的测试结果证明了该方法的有效性。
1 理论与方法
1.1 反射波场与绕射波场的区别
反射波与绕射波的分离需要分析二者的特征差异。Landa等[2]指出:大多数情况下,共偏移距道集上的绕射波和反射波的旅行时曲线(运动学方面)具有较大差异。根据图1a所示的几何观测系统,可写出反射波和绕射波的旅行时曲线方程:
式中:h为半偏移距;zr为反射界面的深度;zd为绕射体的深度;ξ为绕射点在地表投影点xd与中心点xcmp的距离。在共偏移距道集上,半偏移距h一定,反射波旅行时曲线和地下连续反射界面的形状相似,且在大多数地质情况下为局部线性的;而绕射波的旅行时曲线类似于双曲线,如图1b所示。因此,在运动学方面,共偏移距道集上反射波和绕射波旅行时曲线形态的明显差异为两者的分离提供了可能性。

图1 几何观测系统(a)和共偏移距道集上的反射波及绕射波旅行时曲线(b)
1.2 奇异值谱分析理论
奇异值谱分析(SSA)[13]或Cadzow滤波[14]基于线性信号模型来实现线性信号的预测,在地震勘探领域常被用于增强线性信号,压制随机噪声[15]。奇异值谱分析方法的实现步骤主要为:①将数据由时间-空间域变换至频率-空间域;②将频率-空间域信号沿着空间维度转换为Hankel矩阵;③对Hankel矩阵进行SVD分解得到奇异值谱;④根据需要对奇异值谱进行滤波,该滤波处理也称为矩阵降秩处理[16-17]。
基于反射波和绕射波的运动学和动力学特征差异,奇异值谱分析方法可实现绕射波场的分离。连续界面产生的反射波在共偏移距道集上表现为线性特征,如图2a所示。在频率-空间域中,线性信号可以用基函数eiωpx来表达,在规则采样的情况下,第n道信号可以表示为
(3)
式中:L(ω,x1)是频率空间域的参考道信号;ω代表圆频率;p代表射线参数;dx表示道间距。

图2 线性信号模型(a)及其主频对应的Hankel矩阵奇异值分布(b)
地下小尺度地质体产生的绕射波在共偏移距道集上是非线性的,类似于双曲线,如图3a所示。非线性的双曲信号在频率-空间域可以用基函数eiω′p2x2来表达,同样的,在规则采样的情况下,第n道信号可以表示为
(4)
式中:H(ω,xn)是频率-空间域中参考道信号;ω′为时间拉伸后的圆频率[18]。
以5道地震数据模型的Hankel矩阵来说明反射波和绕射波在奇异值谱上的差异,其Hankel矩阵为
(5)
分别将(3)式和(4)式代入(5)式,得到线性信号和非线性信号的Hankel矩阵从(6)式和(7)式可以看出,利用单个线性同相轴构建的Hankel矩阵,其秩为1并且奇异值集中于一点,如图2b所示,同理可以得出线性信号构造的Hankel矩阵,其秩是等于线性同相轴的方向个数[13];利用一个非线性同相轴构造的Hankel矩阵,其秩不为1并且奇异值均匀分布(图3b)。绕射波和反射波运动学特征的不同,使得它们在奇异值谱中具有明显的差异,因此可利用这一特征来进行绕射波和反射波分离。
由SVD理论可知,奇异值谱分析中谱能量是与信号能量强度相关的。强能量的信号有更大的奇异值,并且集中于奇异值谱的第一部分。反射波的能量一般远远强于绕射波的能量,所以它们的奇异值相对更大;绕射波能量相对较小,其奇异值谱值通常集中于谱的中间部分;而随机噪声的谱值通常更小且均匀分布在整个谱上。利用绕射波和反射波动力学特征在奇异值谱上的差异也可实现二者的分离。
数学思维是开启科学大门的钥匙,能为学生的发展指向。在数学教学中,教师要以问题为载体,引领学生发现问题、解决问题,对现实世界中的数量关系、空间形式形成一定的认识。教师要精心设计教学情境,创设教学悬念,引发学生的求知欲望,让学生在分享知识、碰撞智慧中获得发展。
三维情况下,Hankel矩阵M的构建需要y方向的信息,可以表示为
(8)

图3 双曲性信号模型(a)及其主频对应的Hankel矩阵奇异值分布(b)
式中:Ny为y方向线数,分块矩阵M中的子矩阵Mi的构建和二维情况一致。对分块矩阵M进行奇异值谱分析,就可以实现三维情况下绕射波的分离与成像。
1.3 SSA绕射波分离方法的实现
综上所述,在奇异值谱上可以同时基于反射波和绕射波的运动学及动力学特征差异进行二者的分离。类似于奇异值谱分析方法的实现步骤,奇异值谱分析绕射波分离方法的实现过程为:①抽取地震数据转换至共偏移距域;②将同一偏移距内的地震数据转换至频率-空间域,并沿空间维度构建Hankel矩阵,充分表达和突出线性同相轴强能量的反射波;③分别对构建的每一个Hankel矩阵进行SVD分解,得到其奇异值谱;④为实现突出绕射波的目的,去除每一个奇异值谱中较大值的部分,以此来压制全波场中的反射波,进而实现绕射波的分离成像。
必须指出的是,由于奇异值谱各部分并没有完全独立,导致各部分之间存在一定程度上的能量泄露[19],数据试验也说明了该问题。
在实际情况中共偏移距道集中的绕射波难以辨别,而且在复杂地质情况下,反射界面的线性特征也会受到影响,因为奇异值谱的分布与反射波的线性特征关系密切,为此处理时需要考虑在共偏移距道集上加入时窗。时窗的选择需要考虑两个因素:一是共偏移距道集中反射波同相轴的局部线性特征;二是要根据绕射体的深度位置、平均速度、观测系统分布和绕射波时距关系,估算出绕射波在共偏移距道集上非线性同相轴的分布范围。将同一偏移距且同一时窗范围内的地震数据转换至频率-空间域,构建Hankel矩阵,以此适用于实际地质情况。
2 模型数据测试
为验证奇异值谱分析方法应用于绕射波分离和成像的可行性与有效性,首先对模型数据进行测试。图4是模型试验采用的速度模型,其中存在一些孤立的高速绕射体、断层和速度网格化引起的凸点,它们产生弱能量的绕射波。

图4 模型试验采用的速度模型
图5a和图5b分别为分离前的模型数据某原始单炮道集和原始零偏移距道集。图6a和图6b分别为分离后的零偏移距道集和单炮道集。从分离后的零偏移距道集和炮集上可以看到,尽管存在因为奇异值谱部分没有完全分离而产生的能量泄露,但是弱能量的绕射波被明显加强。图7a和图7b 分别为模型数据全波场偏移结果和分离后的绕射波场偏移结果,对比可见,绕射波场偏移结果(图7b)上孤立的高速绕射体、断层以及速度网格化引起的速度变化凸点等绕射体都得到了很好的加强,这将有利于这类小规模地质异常体的识别和定位。
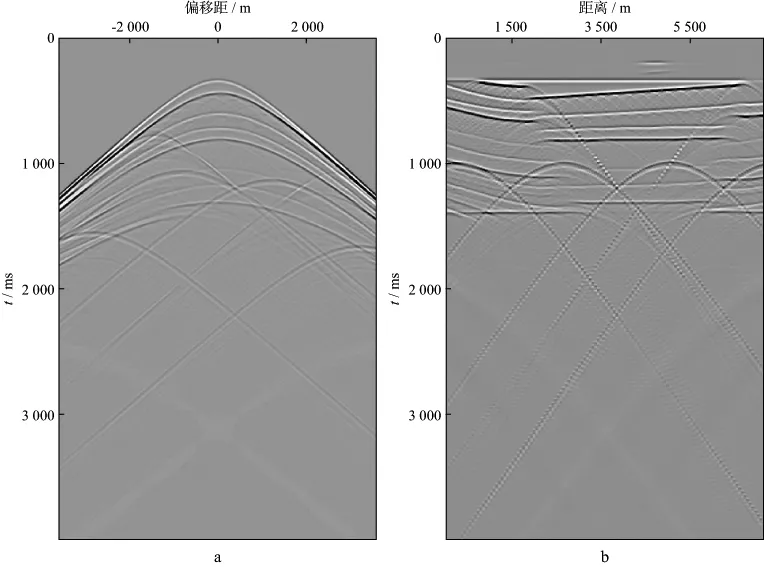
图5 模型数据分离前的原始单炮道集(a)和原始零偏移距道集(b)

图6 模型数据分离后的零偏移距道集(a)和单炮道集(b)

图7 模型数据全波场偏移结果(a)和分离后的绕射波场偏移结果(b)
3 实际资料试验
为了验证奇异值谱分析绕射波分离方法的实际应用能力,采用中国北方某地区实际地震资料进行测试。该地区发育有大量的缝洞型地质构造,传统的成像处理流程难以对这些小地质目标体进行精确成像,为此,利用奇异值谱分析方法对某测线的原始数据进行了反射波和绕射波的分离,然后对绕射波场进行成像。
根据常规处理流程获得的实际资料成像结果,确定出在深度6~7km处存在孤立的缝洞绕射体,根据速度模型确定平均速度为3232m/s,炮道集的接收时间为6s;按观测系统的分布确定绕射点在地表投影点与中心点距离,利用绕射波时距关系式,确定共偏移距道集上炮点在1km范围内满足绕射波非线性同相轴的分布。据此,在共偏移距道集的基础上加入时窗进行实际资料的奇异值谱分析绕射波分离与成像处理。
图8a和图8b分别为分离前实际地震数据的一个原始单炮道集和小偏移距道集。图9a和图9b分别为分离后的单炮道集和小偏移距道集。从分离后的单炮道集(图9a)上可以看到,强能量的反射同相轴被明显压制;在分离后的小偏移距道集(图9b)上,尽管看不到明显的绕射波双曲线,但是强能量的线性反射同相轴被明显减弱。
图10a和图10b分别为该测线原始地震数据全波场偏移结果和分离后的绕射波数据偏移结果(3~8km)。从绕射波场的偏移结果(图10b)上可以清楚地看出,深度在5km左右处的裂缝性绕射体以及6~7km间孤立的缝洞型绕射体的成像结果都被很好地加强。图11为图10中红框部分的局部放大图。对比图11a(图10a的局部放大)和图11b(图10b 的局部放大)中箭头标识处可以看到,经过奇异值谱分析方法的处理,绕射体的成像结果被明显突出,适用于对此类绕射体进行识别和精确定位。
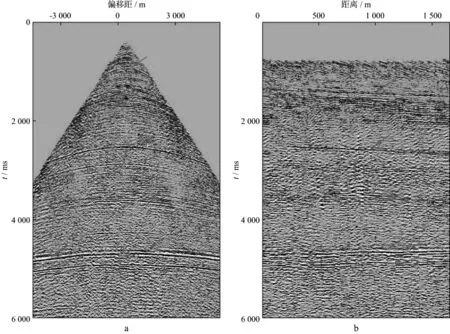
图8 实际地震数据的一个原始单炮道集(a)和小偏移距道集(b)

图9 实际地震数据分离后的单炮道集(a)和小偏移距道集(b)

图10 实际地震数据全波场偏移结果(a)和分离后的绕射波场偏移结果(b)

图11 图10a的局部放大(a)和图10b的局部放大(b)显示结果
4 结论与认识
基于奇异值谱分析的绕射波分离方法同时利用了绕射波和反射波的运动学和动力学特征差异。反射波和绕射波的运动学特征差异表现在共偏移距道集中反射波为线性,而绕射波为非线性;反射波和绕射波的动力学差异表现为前者能量强而后者的能量弱。这些差异导致反射波集中于奇异值谱的第一部分,而绕射波均匀分布于奇异值谱的中部,采用奇异值谱分析的方法可进行反射波和绕射波的分离,进而实现绕射体的目标成像。理论数据和实际资料的测试结果表明,奇异值谱分析绕射波分离方法能够有效突出绕射体的成像。
然而,奇异值谱的分布与反射波的线性特征关系密切,而反射波的线性特征与地下构造的复杂程度有关。奇异值谱分析绕射波分离方法根据等效速度和时距曲线关系,估算绕射波在共偏移距道集上非线性同相轴的分布范围,如何准确把握这之间的关系还需要进一步研究。
致谢:感谢中国石油天然气股份有限公司勘探开发研究院西北分院对本项研究提供的支持。
参 考 文 献
[1] 撒利明,姚逢昌,狄帮让,等.缝洞型储层地震识别理论与方法[M].北京:石油工业出版社,2009:1-212
Sa L M,Yao F C,Di B R,et al.Seismic recognition theory and method of fracture-cave reservoir[M].Beijing:Petroleum Industry Press,2009:1-212
[2] Landa E,Shtivelman V,Gelchinsky B.A method for detection of diffracted waves on common-offset sections[J].Geophysical Prospecting,1987,35(4):359-373
[3] Kanasewich E R,Phadke S M.Imaging discontinuities on seismic sections[J].Geophysics,1988,53(3):334-345
[4] Khaidukov V,Landa E,Moser T J.Diffraction imaging by focusing-defocusing:an outlook on seismic superresolution[J].Geophysics,2004,69(6):1478-1490
[5] Taner M T,Landa E.,Fomel S.Separation and imaging of seismic diffractions using plane-wave decomposition[J].Expanded Abstracts of 76thAnnual Internat SEG Mtg,2006,2041-2045
[6] 孔雪,李振春,黄建平,等.基于平面波记录的绕射目标成像方法研究[J].石油地球物理勘探,2012,47(4):674-681
Kong X,Li Z C,Huang J P,et al,Research of diffraction imaging based on plane-wave record[J].Oil Geophysical Prospecting,2012,47(4):674-681
[7] Fomel S.Applications of plane-wave destruction filters[J].Geophysics,2002,67(6):1946-1960
[8] Reshef M,Landa E.Poststack velocity analysis in the dip-angle domain using diffractions[J].Geophysical Prospecting,2009,57(5):811-821
[9] Landa E,Fomel S,Reshef M.Separation imaging and velocity analysis of seismic diffractions using migrated dip-angle gathers[J].Expanded Abstracts of 78thAnnual Internat SEG Mtg,2008,2176-2180
[10] Asgedom E G,Tygel M,Gelius L J.On separation of reflections and diffractions using a CRS/MUSIC approach[J].Expanded Abstracts of 73rdEAGE Annual Conference,2011,77-81
[11] Berkovitch A,Belfer I,Hassin Y.Diffraction imaging by multifocusing[J].Geophysics,2009,74(6):WCA75-WCA81
[12] Moser T J,Howard C.Diffraction imaging in depth[J].Geophysical Prospecting,2008,56(5):627-641
[13] Sacchi M D.FX singular spectrum analysis[J].CSPG CSEG CWLS Convention,2009,392-395
[14] Cadzow J A.Signal enhancement:a composite property mapping algorithm[J].IEEE Transactions on Acoustics,Speech and Signal Processing,1988,36(1):49-62
[15] 王华忠.波现象与反演成像年度报告集[R].上海:同济大学波现象与反演成像研究组,2012
Wang H Z.WPI annual research report[R].Shanghai:Wave Phenomena and Inversion Imaging,Tongji University,2012
[16] Sacchi M D,Ulrych T J.High-resolution velocity gathers and offset space reconstruction[J].Geophysics,1995,60(4):1169-1177
[17] 崔树果,朱凌燕,王建花.f-x域Cadzow技术分块压制随机噪声及其应用[J].石油物探,2012,51(1):43-50
Cui S G,Zhu L Y,Wang J H.Random noise attenuation with Cadzow technique inf-xdomain and its application[J].Geophysical Prospecting for Petroleum,2012,51(1):43-50
[18] Trickett S.f-xyeigenimage noise suppression[J].Geophysics,2003,68(2):751-759
[19] Nagarajappa N.Coherent noise estimation by adaptive Hankel matrix rank reduction[J].Expanded Abstracts of 82ndEAGE Annual Conference,2012,63-67
