基于Ricker类地震子波的匹配追踪

韩海英，王志章，王宗俊,张雨晴

(1.中国石油大学(北京)地球科学学院，北京102249;2.中国石油天然气股份有限公司勘探开发研究院，北京100083;3.中海油研究总院，北京100027)

近年来，信号时频分解技术在地震资料处理和解释中得到了广泛的应用，如高分辨率处理[1]、烃类检测[2-3]等。常规的时频分解(如窗口傅里叶变换和小波变换等)，时频窗受不确定准则约束，时频分辨率难以同时达到最佳。为了克服常规方法的缺点，Mallat等[4]和Qian等[5]提出了匹配追踪分解算法(Matching Pursuit，MP)。MP算法基于最佳匹配原则，通过不断迭代，从原子库中选取与残余信号结构最佳匹配的原子，将原始信号分解为一系列原子。由于在迭代寻优过程中，时窗长度均由信号局部特征决定，因此这些最优原子反映了信号的局部特征，能较好地描述时变地震信号的时频分布特性。

经典的MP算法基于Gabor函数构建超完备子波库，为了适应信号的不同结构特征，Liu等[6-7]先后提出了基于Ricker子波和Morlet子波的匹配追踪算法。对研究薄互层储层特征而言，Morlet小波分析薄层的效果欠佳;宋新武等[8]认为Ricker子波波形简单，延迟时间短，收敛较快，基于Ricker子波匹配追踪算法的频谱分解技术在薄互层分析中具有较高的时频分辨率，能较好地刻画地质体形态。原子库的合理选取，对于信号的匹配追踪分解效果具有重要作用。

Ricker类地震子波是由Ricker子波演变得到的零相位理论子波，具有3个控制参量，旁瓣能量的收敛速度可变，延迟时间可控，子波库波形更丰富，与地震子波的匹配较为灵活[9]。我们在研究子波波形随3个控制参量变化关系的基础上，对该子波作适当的简化，建立参量与波形特征之间的半定量关系。最后，以简化的子波构建原子库，通过三步法原理[10]实现信号的匹配追踪分解。

1 基本原理

1.1 Ricker类地震子波

Ricker类地震子波频域解析式为[9]

(1)

对于确定的k，m越大，高频能量相对越强;对于确定的m，k越大，高频能量相对越弱，同时频谱的有效频带变窄，导致子波信号的旁瓣变化复杂。文献[9]建议k不宜过大。事实上，参量k和m都是控制波谱高低频相对强弱的参数，一般情况下，相同的增(减)量，m对频谱形态的改变较为平缓。

(2)

这里记C(f)为二参量Ricker类地震子波，简称C子波。其中，fm和c为待定参量;A为归一化系数。通过简化和改写，将子波谱表述成Ricker谱(主频为fm)的c次方(c=1时对应Ricker子波)。fm为波谱主频，控制波谱的等比例伸缩;c控制波谱主频两侧能量的衰减速度。

下面考察参量c与子波波形的关系。首先，针对连续相位数小于1的对称波形(图1中蓝线)，我们定义主、旁瓣极值比PR和主、旁瓣宽度比WR两个参量，用于描述子波的波形特征。

主旁瓣极值比(PR)：旁瓣极值与主瓣极值之比的绝对值;

主旁瓣宽度比(WR)：旁瓣宽度(极小值点间距)与主瓣宽度(零值点间距)之比。

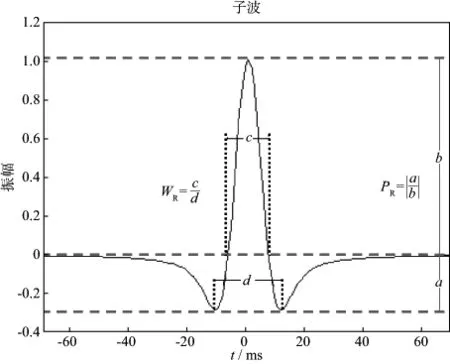
图1 对称C子波示意图解

图2为C子波波形特征值(红色为极值比PR线，蓝色为宽度比WR线)随参量c的变化曲线。随着c的增加，主旁瓣极值比增加，旁瓣能量越强;主旁瓣宽度比增加，说明在相同主瓣宽度的情况下，旁瓣能量达到极值需要的时间变长。因此，对C子波有如下结论：参数fm控制子波的横向伸缩，fm越大，子波越短;参数c控制子波的波形形态，c越大，子波的主旁瓣极值比、宽度比越大，连续相位数增加。当c→0时，C子波趋近于脉冲信号，PR→0，WR→1；当c→∞时，C子波趋近于单频信号，PR→1，WR→2。

图2 主旁瓣宽度比(蓝)和极值比(红)曲线

1.2 基于C子波的匹配追踪

匹配追踪是基于原子库扫描的信号自适应分解。记D为进行信号分解的超完备子波库，可由Hilbert空间的窗口函数通过扩张、调制和平移生成，定义D={wγ:γ=1,2,3,…}，wγ为单个原子，满足归一化条件‖wγ‖=1。记待分解信号为s(t)，经N次迭代分解如下：

(3)

式中：wγ,n为第n次迭代得到的匹配子波;an为wγ,n对应的振幅；RNs为迭代N次后的残差。

匹配追踪算法中子波库的波形与原信号结构越相似，分解效果越好，这里选择C子波来构建匹配子波库。匹配子波wγ,n由参量γn={tn,fm,n,cn,φn}来控制，其中，tn，φn为子波的中心时间和相位;fm,n，cn为波谱控制参量。匹配追踪算法基于不断迭代的贪婪算法，常规算法的每一次迭代都要从子波库中寻找最佳子波。目前，通常采用“三步法”[10]原理来提高分解速度。

(4)

(5)

3) 估算最优子波的幅值。按(6)式得到最优子波的幅值an：

(6)

每一次迭代，都将生成匹配子波anwγ,n和残差信号Rn+1s。分解完成后，即可用提取的匹配子波近似表示原始信号，即

(7)

1.3 时频表征

常规的匹配追踪时频表征通过各匹配子波的Wigner-Ville分布叠加实现，但只能给出振幅分布，无法得到相位信息。这里，采用(8)式所示的时频表征方法[12]，对每个匹配子波的复谱求和，获取信号的时频谱：

(8)

式中：Wγ,n(f)是匹配子波wγ,n(t)的频谱;env[wγ,n(t)]是wγ,n(t)的瞬时包络。

图3是单个C原子(主频fm取50Hz，c取0.7)的时频谱。该时频表征法具有较高的时频分辨率，能同时获取振幅和相位等信息的时频分布，并且避免了窗口截断效应。

图3 C原子时频谱

2 模型试算

设计两个合成信号进行基于C子波库的匹配追踪算法测试，时间采样率均为1ms。

图4为信号1基于C子波的匹配追踪重构结果，其中,图4a为原始信号，图4b为重构信号，图4c 为重构相对误差，重构误差保持在2%以内，对信号的损伤较小(重构精度与算法终止条件有关，精度越高，运行时间越长)。信号组成方式如图5a 所示，其中，第1道为原始信号(图4a)，为其余4道的叠加;图5b为信号1的匹配追踪时频谱。图6a为信号1的短时Fourier变换(STFT)谱，图6b 为S变换谱。对比发现，匹配追踪与常规时频分解方法在分辨率上存在较大的差异。在300ms和400ms处，3个时频谱上都有单个能量团出现，无论是时间尺度还是频率尺度，匹配追踪的分辨率都是最高的;在500ms处，3种方法都没能较好地把两个频率分辨出来，但匹配追踪的时间分辨率还是最高的;在600ms处，S变换和STFT谱的时间分辨率不够，匹配追踪则较好地识别出2个反射;在700ms和800ms处，匹配追踪谱的时频分辨能力明显高于STFT谱和S变换谱，能反映更多的地层薄层信息。因此，匹配追踪时频谱具有较高的时频聚焦性。

图4 信号1重构图解a 原始信号; b 重构信号; c相对误差

信号2(图7)由Ricker类理论子波与随机反射系数褶积生成。为符合实际情况，由浅到深理论子波的主频和带宽逐渐减小，且主频与带宽的比值随机改变。图7a为随机反射系数，图7b为合成记录，从上往下信号的分辨率降低，图7c为匹配追踪结果，图7d为相对误差百分比。为作对比，对信号2同时进行基于Ricker子波的匹配追踪(算法的终止条件不变)，时频谱如图8所示。其中，图8a为图7b基于C子波的匹配分解结果，图8b为基于Ricker子波的匹配分解结果。对比发现，两个分解结果存在一定的差异：C子波匹配追踪谱主频随时间呈近似下降的趋势，符合模型设计，而Ricker子波匹配谱在600ms后主频呈递增的趋势，与实际不符;C子波匹配谱的强能量团与信号的峰值分布符合度较高，如信号2在680～740ms有两个强峰值，C子波匹配谱上有2个强能量团，而Ricker子波匹配谱上则有3个，在800ms附近存在强峰值，C子波匹配谱上存在强能量显示，Ricker子波匹配谱上能量不明显。

图5 信号1的分解结果a 原始信号组成示意; b 基于C子波的匹配追踪时频谱

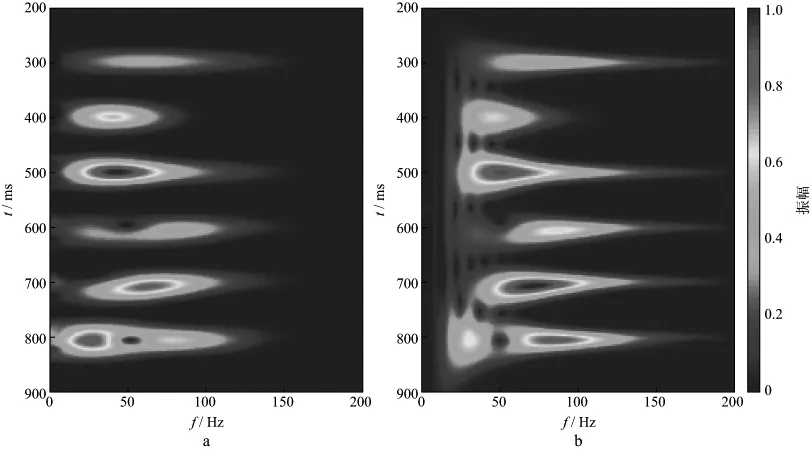
图6 信号1的短时Fourier变换(a)和S变换(b)时频谱

图7 信号2a 反射系数; b 合成记录; c 匹配结果; d 相对误差

图8 信号2匹配追踪时频谱a 基于C子波; b 基于Ricker子波

对比结果表明，匹配追踪的分解效果依赖于原子库与信号基本结构的匹配度。C原子库的参量调控灵活，波形较Ricker子波库丰富，对实际地震信号基本结构(时变地震子波)的适应性更强。因此，对于子波特征值(主旁瓣极值比和宽度比)时变的地震信号，基于C子波的匹配效果优于基于Ricker子波的匹配效果。

3 实际资料处理

图9为陆上某探区的过井测线地震剖面。该区地下构造简单，地层平缓，断裂较少，浅表气遍布全区，第四系沉积以砂泥岩互层为主，成岩性较差，特殊的地质条件造就了该区地震资料的特殊性。经勘探发现该井存在工业气流，综合研究后认为该地区气藏为鼻状构造背景上的岩性气藏。根据以往经验，含油气地区一般会有明显地震异常。从图9 可以看出，在井附近同相轴的连续性变差，有下拉趋势，主频变低，在主测线和联络线上地震相外形呈塔状。这种地震异常虽然存在，但并非特别明显。针对该地区的气藏特征，应用基于C子波的匹配追踪算法，并对资料进行分频处理，为该地区开展岩性气藏研究提供依据。

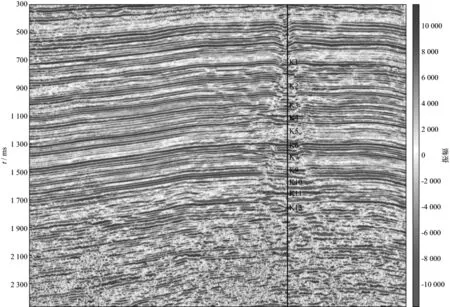
图9 某工区过井测线地震剖面

提取该过井剖面井旁道目的层段(1000～2000ms)地震记录，分别用Ricker原子和C原子对该记录进行匹配追踪，结果如图10所示。对比发现，两种匹配结果都能实现地震信号的高精度匹配分解，较好地反映信号的时频特征;在局部细节上，C原子匹配的时间分辨率优于Ricker原子匹配，如：在1900ms附近(黑框标注部分)，C原子匹配较好地将20Hz主频的两个能量团区分开。因此，利用C原子对地震记录进行匹配追踪，更有助于薄层的精细刻画。

图11是对过井地震剖面进行分频处理得到的单频调谐体剖面，不同频率剖面显示的振幅相对强弱各不相同。通过频率切片，可以清晰地观察到各层位能量不同的展布和变换趋势。图11中黑色横线为气层所处深度(1650ms附近)，观察井(红线)附近目的层的能量，在12Hz左右的分频剖面上达到最大，之后随着频率的增加而降低，这是因为薄层的调谐频率在12Hz左右。在红线与黑线相交位置附近，右侧的能量在12Hz之后逐渐减小，而左侧在25Hz剖面上仍有较强的能量，这是由于右侧含气层的影响。匹配追踪分解结果为目的层油气藏的预测和描述提供了可靠的依据。

图10 过井地震剖面目的层段井旁单道匹配结果a 地震记录; b Ricker原子匹配时频谱; c C原子匹配时频谱

图11 过井地震剖面分频处理得到的单频调谐体剖面

4 结束语

Ricker类子波是一类新型的理论子波，波谱主频以及高低频的衰减速度由三参量联合控制。根据实际需要，将该类子波简化成二参量C子波，波谱主频、带宽由二参量独立控制。针对子波波形，提出以主旁瓣极值比PR和主旁瓣宽度比WR来定量表征，并阐述了C子波波形比Ricker子波、宽带Ricker子波更丰富，更能匹配时变地震子波。

根据C子波建立原子库，用于信号的匹配追踪算法。模型试算表明，与短时Fourier变换和S变换相比，匹配追踪得到的时频谱图具有较好的时频聚焦性;对于时变地震记录，C子波与信号基本结构的匹配度较Ricker子波高，匹配追踪效果更好。最后，将基于C子波的匹配追踪应用于实际资料的分频处理，取得了较好的解释效果。

但同时需要指出的是，基于C子波的匹配追踪算法的运算量较大，运行速度的提升是需要进一步改进优化的方向。

参 考 文 献

[1] 熊晓军，贺振华，黄德济，等．广义S变换在地震高分辨处理中的应用[J]．勘探地球物理进展，2006，29(6)：415-418

Xiong X J,He Z H,Huang D J,et al.Application of generalized S transform in seismic high resolution processing[J].Progress in Exploration Geophysics,2006,29(6):415-418

[2] Castagna J P,Sun S,Siegfried R W.Instantaneous spectral analysis:detection of low-frequency shadows associated with hydrocarbons[J].The Leading Edge,2003,22(2):120-127

[3] Sinha S,Routh P S,Anno P D,et al.Spectral decomposition of seismic data with continuous-wavelet transforms[J].Geophysics,2005,70(6):19-25

[4] Mallat S,Zhang Z.Matching pursuits with time-frequency dictionaries[J].IEEE Transactions on Signal Processing,1993,41(12):3397-3415

[5] Qian S,Chen D.Signal representation via adaptive normalized Gaussian function[J].Signal Processing,1994,36(1):1-11

[6] Liu J,Wu Y,Han D,et al.Time-frequency decomposition based on Ricker wavelet[J].Expanded Abstracts of 74thSEG Annual Internat Mtg,2004,1937-1940

[7] Liu J,Marfurt K J.Matching pursuit decomposition using Morlet wavelets[J].Expanded Abstracts of 75thSEG Annual Internat Mtg,2005,786-789

[8] 宋新武，郑浚茂，范兴燕，等．基于Ricker子波匹配追踪算法在薄互层砂体储层预测中的应用[J]．吉林大学学报(地球科学版)，2011，41(增刊1)：387-392

Song X W,Zheng J M,Fan X Y,et al.Application of the thin-interbedded reservoir prediction based on Ricker wavelet match tracing algorithm[J].Journal of Jilin University(Earth Science Edition),2011,41(S1):387-392

[9] 梅金顺，王润秋．Ricker类地震子波[J]．石油地球物理勘探，2012，47(增刊1)：8-14

Mei J S,Wang R Q.Ricker-like seismic wavelets[J].Oil Geophysical Prospecting,2012,47(S1):8-14

[10] Wang Y.Seismic time-frequency spectral decomposition by matching pursuit[J].Geophysics,2007,72(1):13-20

[11] Barnes A E.Instantaneous frequency and amplitude at the envelope peak of a constant-phase wavelet[J].Geophysics,1991,56(7):1058-1060

[12] 张繁昌，李传辉．非平稳地震信号匹配追踪时频分析[J]．物探与化探，2011，35(4):546-552

Zhang F C,Li C H.Matching pursuit time-frequency analysis of non-stationary seismic signals[J].Geophysical and Geochemical Exploration,2011,35(4):546-552

[13] 张繁昌,李传辉.匹配追踪保幅地震AVF剖面及同频率剖面的构建[J].石油物探,2013,52(3):234-239

Zhang F C,Li C H.Amplitude-preserved AVF and isofrequency section construction based on seismic matching pursuit[J].Geophysical Prospecting for Petroleum,2013,52(3):234-239

[14] 李传辉,张繁昌.地震信号可变分辨率匹配追踪频谱成像方法[J].石油物探,2012,51(3):213-218

Li C H,Zhang F C.Variable resolution matching pursuit spectrum imaging of seismic signals[J].Geophysical Prospecting for Petroleum,2012,51(3):213-218

[15] 张显文,韩立国,王宇,等.地震信号谱分解匹配追踪快速算法及其应用[J].石油物探,2010,49(1):1-6

Zhang X W,Han L G,Wang Y,et al.Seismic spectral decomposition fast matching persuit algorithm and its application[J].Geophysical Prospecting for Petroleum,2010,49(1):1-6

[16] 陈发宇,杨长春.对依据频率的匹配追踪快速算法的改进[J].石油物探,2009,48(1):80-83

Chen F Y,Yang C C.An improvement for frequency-domainated fast matching pursuits algorithm[J].Geophysical Prospecting for Petroleum,2009,48(1):80-83

[17] 赵天姿,宋炜,王尚旭.基于匹配追踪算法的时频滤波去噪方法[J].石油物探,2008,47(4):367-371

Zhao T Z,Song W,Wang S X.Time-frequency filtering de-noise method based on matching pursuit algorithm[J].Geophysical Prospecting for Petroleum,2008,47(4):367-371