曲波域瞬时衰减能量属性在储层识别中的应用研究

郑静静,王延光,刘浩杰

(中国石油化工股份有限公司胜利油田分公司物探研究院,山东东营257022)

地震波在粘弹性介质中传播时,通常会在含流体储层位置出现主频降低、振幅减弱以及高频能量严重衰减等现象[1-2],并可能在储层顶、底形成“亮点”特征。如何利用吸收衰减属性有效识别这些“亮点”特征，是预测含油气储层的关键。常规的“亮点”技术(如提取绝对振幅、振幅包络以及均方根振幅属性等)在地震解释和储层描述中存在一定的局限性与多解性。原因是这些属性只考虑了地震波在时间和频率上的总体变化特征,未考虑地震波的瞬时特性以及振幅衰减随频率变化而变化的特性。为了提高含油气储层的识别精度,我们研究了曲波域衰减能量属性识别储层的方法,给出了曲波域Teager-Kaiser能量属性算法。

曲波变换是由Candès等首先提出的一种基于多尺度脊波变换和带通滤波器的变换方法[3-7]。第一代曲波变换的离散实现比较复杂,包括子带分解、平滑分块、正则化和脊波分析等一系列步骤。2004年,Candès等[8]构造出第二代曲波变换,它无需进行脊波变换,直接在频域定义曲波基的具体形式。2005年,Candès等[9]给出了曲波变换的快速离散算法。曲波变换不但具有多尺度、多方向等特性,而且克服了二维小波变换在表达图像边缘的方向特性等方面存在的内在缺陷[10-15]。

Teager-Kaiser能量算子(TEO)是Kaiser等于1990年提出的一种非线性算子[16],能够突出衰减能量的急剧变化[17],并且分辨率较高。

我们提出的曲波域Teager-Kaiser能量属性算法充分利用了曲波变换的多尺度特性和强局部化功能以及Teager-Kaiser算子的能量聚集性,能够更好地识别特定频段的振幅异常,提高对假“亮点”的识别能力和储层预测的精度。

1 曲波域Teager-Kaiser能量属性计算

1.1 第二代离散曲波变换的基本原理

在离散曲波变换中,笛卡尔坐标下曲波形式为

(1)

(2)

重构公式为

(3)

图1 Curvelet的基本离散框架[18](黑色阴影区域代表一个典型的楔形窗)

1.2 曲波域衰减能量计算方法

Teager-Kaiser能量算子能够有效地提取地震波的局部能量。对于一个有限频带的信号y(n),应用TEO算子可以描述信号在时间点t=nΔt的能量,公式如下:

(4)

其中,m代表物质的离散质量,A代表振幅。

由公式(4)可以看出,TEO是一个与频率和振幅谱平方有关的属性。为了增强算子的稳定性,对1D TEO算子进行推广,得到如下2D TEO公式:

(5)

基于公式(5),推导出曲波域的TEO算子:

(6)

其中,cj,l,k是由公式(2)计算的曲波系数。应用公式(6)对数据进行多尺度分解和能量增强。设曲波变换的分解尺度数为M,每一尺度分解方向数为N,就可以得到下面一系列的数据体：

(7)

公式(7)表示地震波在曲波域的不同尺度和不同方向上的瞬时数据体。对数据体TEOcj,l进行分析比较,寻找瞬时变化最剧烈的数据子体。

(8)

j=1,2,…,M

其中,j代表数据不同尺度下的频率。

利用公式(3)进行曲波反变换,得到一系列能量增强后的多尺度数据体Sj。而在曲波域,直接对每一多尺度数据体应用公式(5)计算瞬时衰减能量,就得到多尺度的衰减能量数据体TEOSj。

2 模型数据测试分析

采用曲波域衰减能量属性识别储层的方法对截取的Marmousi2模型数据进行测试。模型中包含了气层和油层,如图2所示。首先对原始数据进行曲波变换,然后采用公式(6)对曲波域数据进行能量增强,得到一系列的数据体TEOcj,l。图3展示了部分多尺度数据体,从第1尺度到第6尺度，由公式(8)计算瞬时变化最强的能量数据子体,最终得到多尺度的衰减能量数据体，如图4所示。由图4可以看出,随着频率的增加,气层位置能量逐渐变弱,出现明显的高频衰减特征;而油层位置衰减能量先增强,后稍微变弱(能量变化不明显),这与含气储层的特征存在比较明显的区别。分析出现这些明显区别的原因,主要是在地震波的诱导下,含气储层中气体相对流动性较强[19],而含油储层中油的相对流动性非常弱。这种相对运动的差异导致含气储层出现明显的“高频能量衰减,低频能量相对增强”特征[20](如图4中气层位置)，而油层则出现“高频能量衰减较弱,低频能量无相对增强”的特征(如图4 中油层位置)。本文正是利用这种不同频段能量衰减的差异来识别含油、气储层的。

频率逐渐增大。由图3可以看出,经过能量增强之后,气层和油层更加明显。

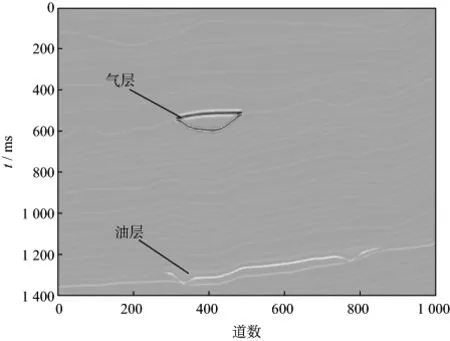
图2 Marmousi2模型局部原始数据

图3 曲波变换、能量增强后的部分多尺度模型数据体(TEOcj,l)a 第1尺度数据; b 第2尺度数据; c 第3尺度数据; d 第4尺度数据; e 第5尺度数据; f 第6尺度数据

图4 模型数据基于曲波变换的多尺度衰减能量(TEO能量)属性剖面a 低频段衰减能量属性; b中频段衰减能量属性; c高频段衰减能量属性

3 实际资料应用试验

应用南方G油田A地区实际地震资料对本文提出的曲波域衰减能量属性预测储层方法的效果进行验证。生物礁滩孔隙-裂缝储集体和岩溶缝洞储集体是该地区两大有利的勘探领域,其中生物礁滩孔隙-裂缝型储层具层控和带状分布的特征,埋深跨度大,为6400～7200m。

图5是实际资料叠后地震剖面,图中实线圈指示位置钻遇气层,虚线圈指示位置钻遇水层。图6是由叠后地震数据提取的瞬时振幅属性,可见图中实线圈和虚线圈指示位置都表现出“亮点”特征,气、水层难以区分,且实线圈中强振幅异常区域较大,显示含气层范围比较大,但钻探揭示实线所示的钻井位置右侧为水层。

图5 实际资料叠后地震剖面

图6 实际资料叠后地震数据的瞬时振幅属性

为了正确识别区分气、水层,首先通过曲波变换将地震数据变换到曲波域,应用公式(6)对曲波系数进行能量增强,得到一系列的能量增强数据体TEOcj,l;然后将一系列的TEOcj,l数据体划分为高、中、低3个频段的数据体,在每一个频段内应用公式(8)计算瞬时变化最剧烈的数据子体,最后得到多尺度的衰减能量数据体。图7a是低频段(<15Hz)衰减能量属性剖面;图7b是中频段(<35Hz)衰减能量属性剖面;图7c是高频段(<50Hz)衰减能量属性剖面。

对于图6所示瞬时振幅剖面上显示为“亮点”特征的实线圈中区域，在低频段剖面(图7a)上显示为两个储层,左边储层显示出强能量衰减特征,中频段剖面上(图7b)振幅能量减弱,高频段剖面上(图7c)衰减能量进一步变弱,显示出强的“高频能量衰减”特征,与含气储层特征一致;实线圈中右边的储层振幅能量在低频剖面上相对较弱,随着频率的增加显示出能量稍有增强的特征,这与含气或含油储层特征不符,判定为假“亮点”。对于图6瞬时振幅剖面上同样显示出“亮点”特征的虚线圈中区域,在低频段的图7a中基本没有能量显示,随着频率的增大,振幅能量增强(图7b和图7c),且中频段到高频段能量变化不大,并未显示出任何的衰减特征,因此可以判定为水层的假“亮点”显示。因为在地震波的传播过程中含水层几乎无流体相对运动,也就几乎不存在“高频能量衰减”的特点。实际生产情况表明,图7中实线圈内区域分为两个储层,左边为含气层,右边为非油气储层;而虚线圈内区域为水层，与预测结果非常吻合。

为了进一步验证曲波域衰减能量属性预测储层方法的效果,我们针对上述实际资料再采用常规的时频分析技术提取出多尺度衰减能量属性剖面(图8)进行对比分析。图8a是低频段(<15Hz)衰减能量属性剖面;图8b是中频段(<35Hz)衰减能量属性剖面;图8c是高频段(<50Hz)衰减能量属性剖面。由图8可见,实线圈内区域在低频段剖面(图8a)上也显示出强能量衰减特征,且随着频率增大到中频段(图8b),振幅能量减弱；到高频段(图8c)时衰减能量进一步变弱,显示出强的“高频能量衰减”特征,与含气储层特征一致。同时,虚线圈中区域在低频段的图8a中基本没有能量显示,随着频率的增大,振幅能量逐渐增强(图8b和图8c),由此可以判定为假“亮点”。但是,在低频段剖面(图8a)上实线圈中区域并未显示出两个储层,在中频段剖面(图8b)上两个储层也未明显分开,而只在高频段剖面(图8c)中可以看出有两个储层。即随着频率的增加,实线圈内右边的非油气储层在基于常规时频分析技术的衰减能量属性剖面上未能明确显示出振幅能量随频率增加而增强的特征。

图7 实际资料基于曲波变换的多尺度衰减能量属性剖面a 低频段衰减能量属性; b 中频段衰减能量属性; c 高频段衰减能量属性

对比分析图7和图8可以看出,基于常规时频分析和基于曲波变换的衰减能量属性都能较为有效地识别气层和水层,但曲波域能量衰减属性更为准确可靠。

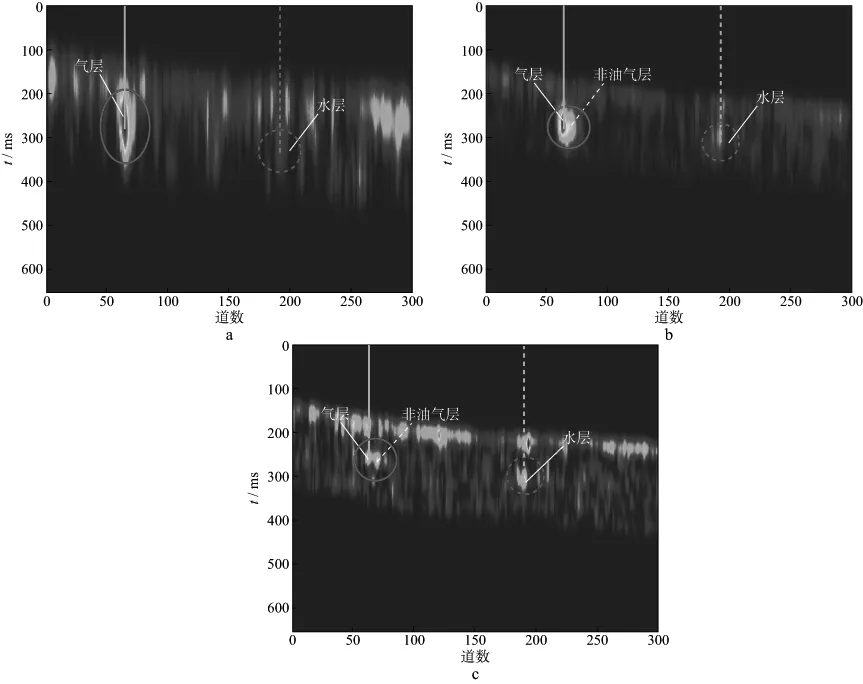
图8 实际资料基于常规时频分析技术的多尺度衰减能量属性剖面a 低频段衰减能量属性; b 中频段衰减能量属性; c 高频段衰减能量属性

4 结束语

基于地震波传播时出现的“高频衰减”特征,提出了利用曲波域衰减能量属性进行储层预测的方法。该方法充分利用了曲波变换的多尺度特性和非线性Teager-Kaiser算子的能量聚集性,有效突出了特定频带强衰减能量的急剧变化，能够有效地识别含不同流体储层引起的强振幅异常特征,准确区分气、水层。曲波域衰减能量属性的提出为真、假“亮点”的识别提供了一种新的判别方法,与其它油气检测方法配合使用,有助于减小储层预测的误差。

参 考 文 献

[1] 王小杰,印兴耀,吴国忱.基于S变换的吸收衰减技术在含气储层预测中的应用研究[J].石油物探,2012,51(1):37-42

Wang X J,Yin X Y,Wu G C.The application of an S transform based absorption and attenuation technique for prediction of gas-bearing reservoir[J].Geophysical Prospecting for Petroleum,2012,51(1):37-42

[2] 魏文,王兴谋,李红梅,等.基于地震波衰减的特征属性重构方法[J].石油物探,2012,51(3):219-225

Wei W,Wang X M,Li H M,et al.Method of characteristics attributes reconstruction based on seismic wave attenuation[J].Geophysical Prospecting for Petroleum,2012,51(3):219-225

[3] Candès E J,Donoho D L.Curvelet a surprisingly effective nonadaptive representation for objects with edges[M].TN:Van-derbilt University Press,1999:1-30

[4] Candès E J.Ridgelets:theory and applications[D].USA:Department of Statistics,Stanford University,1998

[5] Candès E J,Donoho D L.Ridgelets:a key to higher-dimensional intermittency?[J].Philosophical Transactions of the Royal Society of London Series A:Mathematical and Physical Sciences,1999,2495-2509

[6] Do M N,Vetterli M.The finite ridgelet transform for image representation[J].IEEE Transactions on Image Processing,2003,12(1):16-28

[7] Donoho D L.Fast ridgelet transforms in dimension 2 [R].California:Department of Statistics,Stanford University,1997

[8] Candès E J,Donoho D L.New tight frames of curvelets and optimal representations of objects with piecewise-C2 singularities[J].Communications on Pure and Applied Mathematics,2004,57 (2):219-266

[9] Candès E J,Demanet L,Donoho D L,et al.Fast discrete curvelet transforms[J].Applied and Computational Mathematics,2005:1-43

[10] 张广智,郑静静,印兴耀．基于Curvelet变换的多尺度性识别裂缝发育带[J]．石油地球物理勘探,2011,46(5):757-762

Zhang G Z,Zheng J J,Yin X Y.Identification technology of fracture zone and its strike based on the Curvelet transform[J].Oil Geophysical Prospecting,2011,46(5):757-762

[11] 郑静静,印兴耀,张广智.基于Curvelet 变换的多尺度分析技术[J].石油地球物理勘探,2009,44(5):543-547

Zheng J J,Yin X Y,Zhang G Z.Multi-scale analysis techniques based on the Curvelet transform[J].Oil Geophysical Prospecting,2009,44(5):543-547

[12] Zheng J J,Yin X Y,Zhang G Z,et al.The surface wave suppression using the second generation Curvelet transform [J].Applied Geophysics,2010,7(4):325-335

[13] 张广智,郑静静,印兴耀,等.基于Curvelet变换的角度流体因子提取技术[J].物探与化探,2011,35(4):505-509

Zhang G Z,Zheng J J,Yin X Y,et al. The technique for extracting angle fluid factor based on Curvelet transform[J].Geophysical and Geochemical Exploaration,2011,35(4):505-509

[14] 刘伟,曹思远,王征,等.基于贝叶斯阈值估计的曲波域自适应随机噪声衰减[J].石油物探,2013,52(2):115-120

Liu W,Cao S Y,Wang Z,et al.The self-adaptive random noise attenuation in curvelet domain based on Bayes estimation[J].Geophysical Prospecting for Petroleum,2013,52(2):115-120

[15] 姜宇东,杨勤勇,何柯,等.基于曲波变换的地面微地震资料去噪方法研究[J].石油物探,2012,51(6):620-624

Jiang Y D,Yang Q Y,He K,et al.Surface microseismic date denoising method based on curvelet transform [J].Geophysical Prospecting for Petroleum,2012,51(6):620-624

[16] Kaiser J F.On a simple algorithm to calculate the energy of a signal[C]// Proceedings of IEEE International Conference on Acoustics.Speech and Signal Processing (ICASSP’90).Albuquerque:IEEE Computer Society,1990:381-384

[17] Bahoura M,Rouat J.Wavelet speech enhancement based on the Teager energy [J].IEEE Signal Processing Letters,2001,8(1):10-12

[18] Herrmann F J,Wang D L,Hennenfent G,et al.Seismic data processing with curvelets:a multiscale and nonlinear approach[J].Expanded Abstracts of 77thAnnual Internat SEG Mtg,2007,2220-2224

[19] 李红梅.基于孔隙粘弹性介质的AVO正演模拟及衰减分析[J].石油物探,2013,52(5):464-474

Li H M.AVO forward modeling and attenuation analysis based on porous viscoelastic media[J].Geophysical Prospecting for Petroleum,2013,52(5):464-474

[20] 刁瑞,李振春,韩文功,等.基于广义S变换的吸收衰减分析技术在油气识别中的应用[J].石油物探,2011,50(3):260-265

Diao R,Li Z C,Han W G,et al.Application of absorption attenuation analysis technique based on generalied S transform for hydrocarbon identification[J].Geophysical Prospecting for Petroleum,2011,50(3):260-265