微地震震源矢量反演

宋维琪,徐奔奔,杨勤勇,郭全仕,姜宇东,喻志超,秦 晅

(1.中国石油大学(华东)地球科学与技术学院,山东青岛266580;2.中国石油化工股份有限公司石油物探技术研究院,江苏南京211103)

震源反演问题源于天然地震。微地震震源反演问题和天然地震震源反演问题本质上是相似的,但由于形成震源的机制不同,因此其具体实现方法不同。天然地震震源是构造活动引起地层错动而产生强烈的地震波,属于断裂活动震源。微地震震源是压裂后岩石破裂,释放能量产生地震波[1]。在接收点观测的微地震记录是地层、震源和其它干扰因素的综合响应叠加结果。一般在地层速度均匀或横向均匀、震源为均匀辐射点源(辐射能量大小在各个方向相同)情况下,利用观测记录计算的事件的方位角和震源的方位角相同。如果地层速度横向变化或震源为非均匀辐射,则事件的方位角和震源的方位角不同。要实现事件的高精度定位,必须去除或校正掉地层的横向变化效应和震源辐射的非均匀效应。研究源辐射的非均匀性问题,属于震源反演问题[2]。

正演是反演的基础,考虑到实际反演需要,一般采用射线追踪方法进行正演。对于宽入射角接收的微地震射线追踪正演,基本采用走时模拟,基于射线追踪[3]的微地震高精度振幅、相位正演模拟很少,而这直接又关系到方位角反演的准确性。勘探地震领域研究的AVO反射系数近似计算公式,是在限定角度下推导的。对于宽入射角透射、反射系数的计算,还没有实际有效的方法。本文采用简化的高斯束射线追踪方法[4]进行正演。

随着微地震监测技术的发展,关于微地震震源机制及反演问题的研究也逐渐增多,但大多只注重某一方面。本文从地层响应效应、检波器定位及震源等方面进行系统研究,提出了新的研究思路和技术方法。

1 地震震源矩张量、张量分析

矩张量反演已成为现今天然地震主要的震源机制求解方法[5],一般采用力偶源组合震源模型。矩张量存在9个矩张量分量,表示为

(1)

矩张量具有对称性,因此存在6个独立分量。如果能够获得这6个独立分量的值,就可以确定震源机制的3个轴(P,T,B轴)；同时,根据震源机制轴面之间的位置关系,相应的节面空间位置也得到确定。矩张量反演就是为了确定6个独立矩张量的值,震源传播方程可以写作[6]

(2)

其中,U是地震波传播到地面时检波器接收到的位移序列;格林函数G描述地层介质因素;M是6个独立分量序列。(2)式把记录到的地震信号很好地分成了震源和地层介质两个因素。通过记录到的位移和格林函数可以反演得到6个独立的矩张量。6个独立的矩张量如果为纯双力偶的情况,就可以求解矩张量的3个特征向量,这3个特征向量对应震源机制的P,T,B3个轴。

震源可以看成是一个不连续的点,也可以看作一个双力偶源。作为一个双力偶源时,可以用一个矩张量表示,即

(3)

式中：M0为等效体力；ni为断层面法向方向力在x,y,z方向的分量;fi为断层面滑动方向力在x,y,z方向的分量。因此矩张量又表示为

(4)

如果不考虑标量矩M0问题,只考虑点源能量不同方向的变化问题,利用张量研究震源,则为[7]

(5)

如果只考虑3个主(优势)方向,则为

(6)

本文采用矢量研究微地震震源反演问题。

2 格林函数正演

2.1 基本方法

矢量反演以地下震源传播到接收点上的位移能够被矢量描述为前提,接收点记录是震源矢量和地层传播矢量的综合响应结果。为了进行震源反演,必须首先研究正演问题,利用简化高斯束射线追踪方法合成地震记录。微地震监测观测到的微地震记录是宽角地震记录,因此我们讨论宽角激发、接收条件下的微地震正演合成记录。

位移的一般表示式为[8]

(7)

其中

(8)

式中：A(R),A(S)为接收点和源点的振幅;ρ(R),ρ(S)为接收点和源点的密度;v(R),v(S)为接收点和源点的速度;βi,αi是上、下地层P,P′界面两侧以地层界面的切线方向为水平轴的局部坐标系中入射线和透射线与局部坐标系x正方向的夹角;Ti为透射系数。

采用Zoeppritz方程计算透射系数,Zoeppritz方程的矩阵形式为[9]

(9)

式中：α,β,α′,β′分别表示反射P波和反射SV波、透射P波和透射SV波的角度;RPP和RPS是以位移表示的反射P波和反射SV波反射系数;TPP和TPS分别是以位移表示的透射P波和透射SV波透射系数;vP1,vP2,vS1,vS2分别表示下层介质的P波速度、上层介质的P波速度、下层介质的SV波速度、上层介质的SV波速度;ρ1,ρ2分别表示上、下层介质的密度。

合成地震记录为

(10)

式中：φ0,φN为中心射线的入射角范围,包括所有对检波点R有贡献的高斯射线束;g(R,φ)是波包;Δφ表示中心射线的角度间隔[10]。

2.2 正演结果

正演采用均匀水平层状速度模型,震源子波为雷克子波,10级三分量检波器接收。为了体现震源能量在观测位移分量上的变化,设计了均匀震源和非均匀震源。正演模拟结果如图1所示,在呈现地层响应变化的同时,呈现了震源的能量变化引起的位移变化,可见震源非均匀性辐射引起微地震记录振幅发生较大变化。

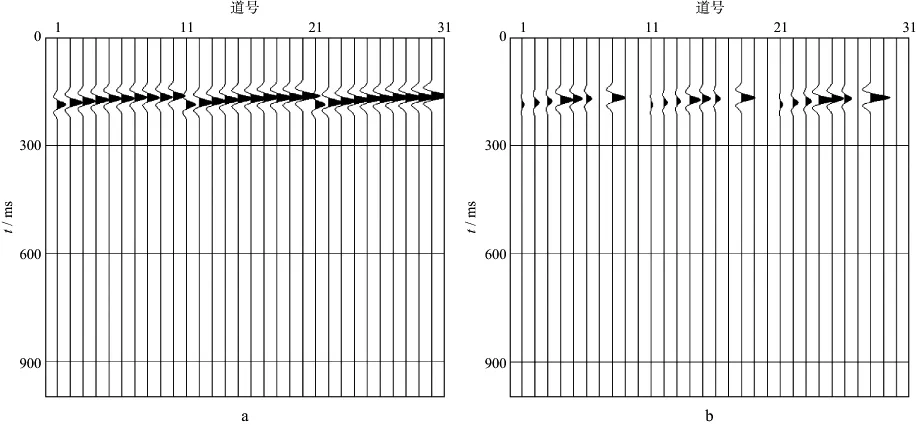
图1 正演模拟结果a 均匀点源合成记录; b 非均匀点源合成记录

3 微地震矢量反演

3.1 基本方法

反演的基本思想是通过对比观测的微地震波场运动学和动力学记录与理论模型正演波场的运动学和动力学波场信息,利用迭代方法[11]反演震源参数。

为了得到准确的震源矢量反演结果,建立贴近实际的初始模型至关重要。反演模型包括源-检位置、地层速度模型和震源矢量模型。为了使求解过程快速收敛且得到较高精度的解,提出如下反演策略：①利用走时反演得到震源位置、计算格林函数;②对地层速度和震源位置进行微调反演,对震源矢量进行调节反演。

3.2 基于走时的距离反演

要获得震源到接收点的格林函数,需反演得到震源和接收点间的距离[12]。为此,在基于走时的距离反演基础上,利用黄金分割法进行搜索,并且在对数域进行寻优反演,以提高反演精度。具体步骤如下：

1) 设置计算区间[a1,b1]=[Rmin,Rmax],[c1,d1]=[zmin,zmax]及精度要求ε>0,计算搜索网格点R1=a1+(1-0.618)(Rmax-Rmin),z1=c1+(1-0.618)(zmax-zmin),计算目标函数值fk,并令k=1。计算目标函数时走时取对数,即fk=lg(|Ti-Tj|)。

2) 如果|fk+1-fk|<ε,则停止计算,否则转步骤3)。

3) 置ak+1=Rk,ck+1=zk,bk+1=bk,dk+1=dk,ak+1=Rk+1+0.618(bk+1-ak+1),ck+1=zk+1+0.618(dk+1-ck+1),计算目标函数值fk。如果|fk+1-fk|<ε则停止计算,否则转步骤4)。

4) 置k=k+1,转步骤2)。

图2为某一实际微地震事件的走时及走时差,图3和图4为利用改进后的算法分别在算数域和对数域进行的距离反演结果。通过对比可以看出,在径向方向上,对数域反演结果较为收敛和精确。

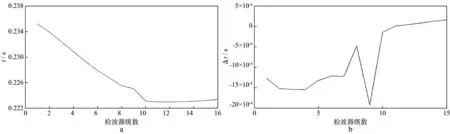
图2 各道走时(a)和相邻道走时差(b)

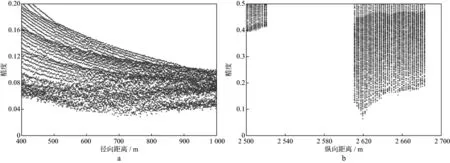
图3 算数域反演结果a 径向方向; b 纵向方向

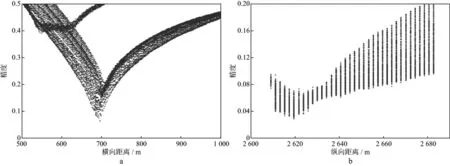
图4 对数域反演结果a 径向方向; b 纵向方向

3.3 震源矢量反演

3.3.1 震源矢量模型建立

利用偏振分析技术,通过观测的三分量记录得到特征向量进而得到总的观测主矢量;利用格林函数正演得到地层速度、源-检位置格林函数矢量。将偏振分析得到的矢量去除格林矢量后作为震源初始矢量模型。

3.3.2 反演寻优方法

利用模拟退火方法[13]进行反演,参与反演调节的模型为矢量模型。

3.3.3 目标函数的确定

三分量检波器坐标虽然利用射孔资料进行了标定,但是由于射孔源的非均匀性、地层效应、检波器响应及其它干扰因素的影响,标定结果很不准确。所以,作为三分量振幅反演,不但要进行速度模型调节、震源辐射能量[14]调节反演,还要进行三分量检波器坐标的标定调节反演。只有在检波器坐标确定的条件下,才能得到振幅在其上的准确投影分量。格林函数地层响应的极化矢量为AG,通过格林函数正演求得,震源的极化矢量为AS,总的极化矢量为A=AG+AS,则理论模型计算的3个分量为

(11)

式中：φ0是极化矢量的倾角,是确定的,因为三分量检波器垂直分量的方向是固定的;α0是检波器水平分量的初始方位角,与射孔标定精度有关,是不确定的。α=αs-α0,αs是事件s的方位角。

由于同一个事件对于多级检波器的绝对方位角(事件方位角与检波器初始方位角的差)是相同的,因此,反演目标函数加入了多级检波器绝对方位角相等的约束条件,以使反演解得到更好的控制。即

(12)

式中：i是检波器级数,j是相邻事件个数序号。

最终反演目标函数为

(13a)

αij=αs,i,j-α0,j=αi+1,j=αs,i+1,j-α0,j

i=1,2,…,N-1

j=1,2,…,K

(13b)

式中：Ux,g,Uy,g,Uz,g表示实际观测的3个分量；p为模数。

为了建立三分量检波器较准确的坐标系,利用多个射孔资料进行矢量反演,具体步骤如下：

1) 利用走时距离反演结果及建立的速度模型,进行格林函数正演;

2) 令k=1;

3) 将原走时距离反演建立的速度模型作为初始速度模型,源矢量反演时对其进行微调,即v=v0+Δv;

4) 震源矢量调节,对观测的三分量数据进行偏振分析,将求得的偏振矢量作为矢量反演的初始矢量模型,在此基础上进行扰动调节,即As=As0+ΔAs;

5) 检波器初始方位角调节,将射孔资料计算的检波器方位角作为初始方位角,在反演过程中进行不断调节,即α0=α0,s+Δα0;

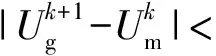
7)k=k+1,转向步骤3);

8) 停止计算。

4 理论模型验证分析

采用均匀水平层状模型验证了震源矢量反演方法的正确性。设置模型事件方位角为60°,震源位置(200m,-200m,1000m),井下垂直10级三分量检波器接收,第1级检波器接收位置(0,0,950m),各级检波器之间的距离为20m。为了验证源矢量方向和方位方向的不一致,采用能量大小不同、方向不同的3个源矢量合成一个总的源矢量,合成矢量方向方位角见表1。对合成记录进行偏振分析求得各级检波器方位角,再进行震源矢量反演,结果如表1所示。分析模型和反演结果可见,通过合成记录计算的方位角和模型方位角差距较大,震源反演的方位角基本上接近模型合成矢量方位角。说明震源矢量反演方法正确,反演结果具有较高的精度。

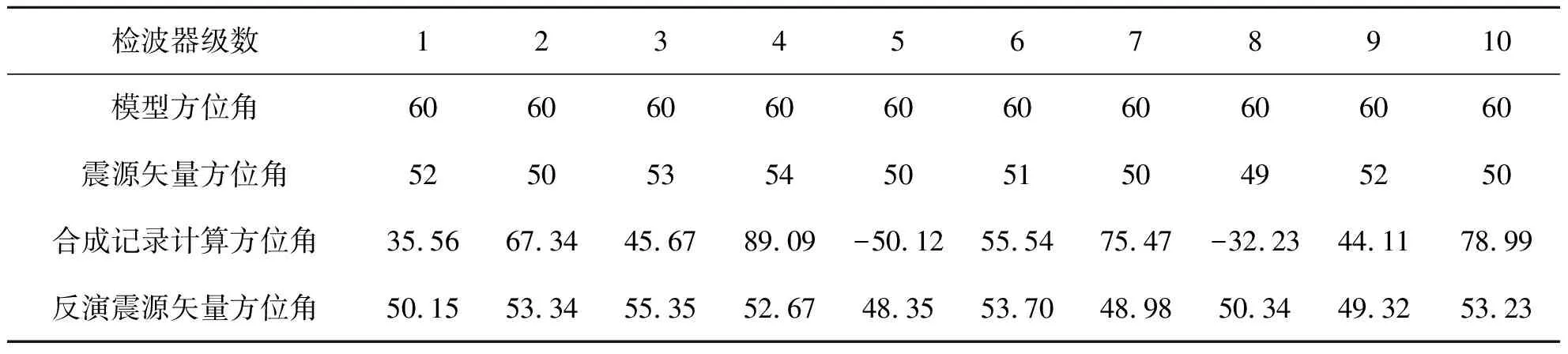
表1 均匀水平层状模型分析结果 °

5 实际资料验证分析

利用某油田压裂微地震监测资料进一步验证震源矢量反演方法的正确性。该区压裂井和监测井两井之间的距离为657.8m,目的层段深度2130.0m,压裂岩石岩性为灰岩。采用12级三分量检波器接收,各级检波器之间的距离为10m,硬链接3级,间距为4.5m。图5a为直接反演定位结果,图5b为震源矢量反演方法定位结果。

研究区压裂目的层岩性较均匀,压裂裂缝的发育主要受控于水压力和地应力围压分布,主构造发育方向近似为东北方向;又由井资料可知,目的层最大主应力方向为东北方向。据此推断,在水力压力和地应力作用下,岩石破裂裂缝的延伸方向应该为东北方向。该区压裂射孔点平面位置在(257m,10m)处,对比分析图5a和图5b可见,直接反演定位结果的射孔点附近事件分布稀疏,而射孔点附近以外事件分布较稠密,不符合压裂微地震事件发育分布规律;通过震源矢量反演再定位后,射孔点附近事件分布稠密,而射孔点附近以外事件分布稀疏,这与压裂微地震事件发育分布规律相符。

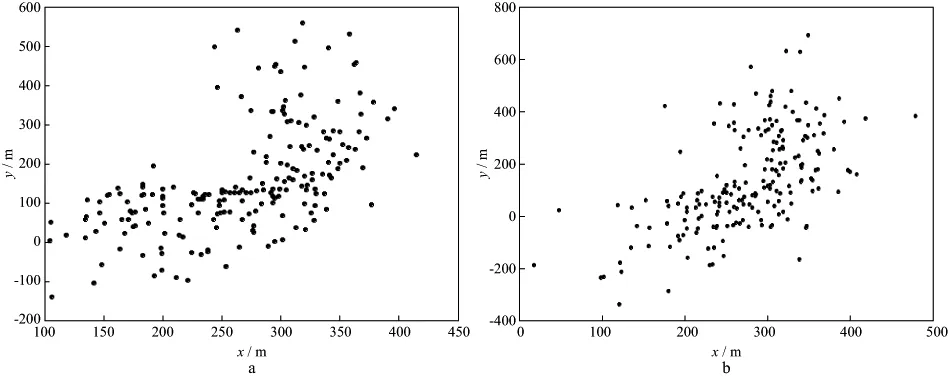
图5 某油田压裂微地震定位结果a 直接反演定位结果; b 震源矢量反演定位结果

6 结束语

微地震震源矢量反演方法定位结果较直接反演方法定位结果在精度和可靠程度方面有了较大提高。这是因为：①利用简化的高斯束射线追踪方法合成地震记录,走时和振幅精度能够满足反演的要求;②改进了走时距离反演,将以往的常规网格搜索方法改进为黄金分割网格搜索方法;③在对数域进行走时正演和反演迭代计算,提高了径向距离对走时的敏感性;④在进行速度模型反演调节、震源辐射能量反演调节时,利用多个射孔资料进行三分量检波器坐标的标定调节,得到了相对准确的检波器坐标方位;⑤根据同一个事件对于多级检波器的绝对方位角相同,反演目标函数增加了多级检波器绝对方位角相等的约束条件,使反演结果更加可靠。

参 考 文 献

[1] 宋维琪,陈泽东,毛中华.水力压裂裂缝微地震监测技术[M].北京：中国石油大学出版社,2008:156-167

Song W Q,Chen Z D,Mao Z H.Hydro-fracturing break microseismic monitoring technology[M].Beijing:China University of Petroleum Press,2008:156-167

[2] 许冲,徐锡伟,于贵华.基于证据权方法的玉树地震滑坡危险性评价[J].地震地质,2013,35(1):151-164

Xu C,Xu X W,Yu G H.The Yushu earthquake triggered landslide hazard evaluation based on weight of evidence method[J].Seismology and Geology,2013,35(1):151-164

[3] 谢飞,李佩,黄中玉,等.高斯射线束叠前深度偏移成像研究[J].石油物探,2013,52(1):65-71

Xie F,Li P,Huang Z Y,et al.Gaussian beam prestack depth migration[J].Geophysical Prospecting for Petroleum,2013,52(1):65-71

[4] 黄建平,张晴,张凯,等.格林函数高斯束逆时偏移[J].石油地球物理勘探,2014,49(1):101-106

Huang J P,Zhang Q,Zhang K,et al.Reverse time migration with Gaussian beams based on the Green function[J].Oil Geophysical Prospecting,2014,49(1):101-106

[5] Engell-Sorensen L.Inversion of arrival times of microearthquake sources in the North Sea using a 3-D velocity structure and prior information,part I:method[J].Bulletin of the Seismological Society of America,1991,81(4):1183-1194

[6] Oladapo M I.Linearization of Zoeppritz equations and practical utilization[J].International Journal of Physical Sciences,2013,8(24):1298-1306

[7] Prugger A F,Gendzwill D J.Microearthquake loca-tion:a nonlinear approach that makes use of a simplex stepping procedure[J].Bulletin of the Seismological Society of America,1988,78(2):799-815

[8] 安艺敬一,理查德.定量地震学:理论与方法[M].北京:地震出版社,1980:365-398

Aki K,Richards P G.Quantitative seismology:theory and methods[M].Beijing:Seismological Press,1980:365-398

[9] McMechan G A.Migration by extrapolation of time-dependent boundary values [J].Geophysical Prospecting,1983,31(3):413-420

[10] Furumura T,Kennett B,Takenaka H.Parallel 3-D pseudospectral simulation of seismic wave propagation[J].Geophysics,1998,63(1):279-288

[11] Blake B,Figueroa D,Hofland G,et al.3D forward ray trace seismic modeling of strike lines in complex geology[J].Expanded Abstracts of 69thAnnual Internat SEG Mtg,1999,1871-1874

[12] Kummer B,Behle A,Dorau F.Hybrid modeling of elastic-wave propagation in two-dimensional laterally inhomogeneous media[J].Geophysics,1987,52(6)：765-771

[13] Stoffa P L,Sen M K.Nonlinear multiparameter optimization using genetic algorithms:inversion of plane-wave seismograms[J].Geophysics,1991,56(11):1794-1810

[14] Pei D,Quirein J A,Cornish B E,et al.Velocity calibration for microseismic monitoring:a very fast simulated annealing (VFSA) approach for joint-objective optimization[J].Geophysics,2009,74(6):WCB47-WCB55