一类时间分数阶延迟微分方程的数值解法

张艳敏, 郭 萍, 段素芳

(青岛理工大学 琴岛学院, 山东 青岛 266106)

自然界中自然科学和工程领域的很多现象都可以归结为延迟微分方程模型.时间分数阶延迟微分方程是一类重要的方程,时间分数阶微分方程能更好地描述一些反常现象、多孔介质等问题的发生过程.由于这些微分方程的精确解很难获得,所以对数值方法的研究就非常重要,但是目前对时间分数阶延迟微分方程的研究文献还较少[1-5],数值方法的研究就更少了[4-5].

本文考虑如下初值时间分数阶延迟微分方程:

式中,0<α<1;a,b,τ,T是正的常数;f(t),ψ(t)为已知连续函数.时间分数阶导数为Caputo分数阶导数[6].

1 差分方程的构造

y(tn)=ψ(tn) (n=-p,-p+1,…,-1,0).

(3)

将式(1)在tn+1处离散后得差分方程为

记ωk=(k+1)1-α-k1-α,γ1=b(Δt)αΓ(2-α),

γ2=a(Δt)αΓ(2-α),qn+1=(Δt)αΓ(2-α)fn+1,

对式(4)化简得

(5)

通过式(5),可以将方程(1)分情况写成如下两个差分方程:

2 差分格式稳定性的证明

定理1 差分方程(6)、(7)是无条件稳定的.

证明 由ωk=(k+1)1-α-k1-α易得

1=ω0>ω1>…>ωk>ωk+1>…>0,

由式(6)和式(7)得误差格式为

则当n=1时,由式(8)得

假设当n≤k时

|εk|≤(1+γ2)k|ε0|

成立,则当n=k+1时,由式(9)得

3 差分格式收敛性的证明

记y(tn)为精确解,yn为式(6)和式(7)的解,误差为en=y(tn)-yn,则由式(2)和式(3)知,当-p≤n≤0时,en=0.由局部截断误差的定义以及式(3)、式(6)、式(7)得

式中,Rn为局部截断误差.

由泰勒公式和积分中值定理[7-8]易得,存在常数P>0,使得|Rn|≤PΔt.

定理2 差分方程(6)、(7)是无条件收敛的.

证明 当n=1时,由式(10)得

式中,C=(Δt)α+1Γ(2-α)P.

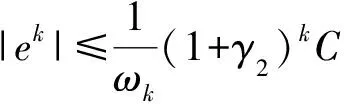
|ek+1|≤(1+γ1)|ek+1|≤

(Δt)αΓ(2-α)|Rk+1|≤

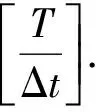
4 数值算例

考虑如下算例:

其精确解为y(t)=t+1,此时,方程(1)中a=b=2,分别取时间步长为0.1,0.01,0.005,0.001,数值计算结果如表1所示.

表1 数值解的相对误差Table 1 Relative errors of numerical solutions

从相对误差可以得出本文给出的数值解法是解决此类问题的一种有效的方法.

参考文献:

[1]伊婕. 变分迭代法关于Caputo分数阶常微分方程和中立型比例延迟微分方程的收敛性分析[D]. 湘潭:湘潭大学, 2010.

(Yi Jie. Convergence of Variational Iteration Method for Caputo Fractional Differential Equations and Neutral Differential Equations with Pantograph Delay[D]. Xiangtan: Xiangtan University, 2010.)

[2]杨水平. 关于分数阶多阶延迟微分方程的解的存在性[J]. 惠州学院学报:自然科学版, 2011,31(3):29-31.

(Yang Shuiping. The Existence of Solutions for Multi-order Fractional Differential Delay Equation[J]. Journal of Huizhou University: Natural Science, 2011,31(3):29-31.)

[3]潘新元. 两类分数阶延迟微分方程及其数值方法的渐近稳定性[D]. 湘潭:湘潭大学, 2009.

(Pan Xinyuan. The Asymptotic Stability of Types Fractional Order Delay Differential Equations and Some Numerical Methods[D]. Xiangtan: Xiangtan University, 2009.)

[4]冯日月. 分数阶延迟微分方程数值方法的研究 [D]. 哈尔滨:哈尔滨工业大学, 2009.

(Feng Riyue. Numerical Methods for Differential Equations of Fractional Order with Time-Dependent Delay[D]. Harbin: Harbin Institute of Technology, 2009.)

[5]马亮亮. 变系数空间分数阶对流-扩散方程的有限差分解法[J]. 沈阳大学学报:自然科学版, 2013,25(4):341-344.

(Ma Liangliang. Finite Difference Methods for Space Fractional Convection-diffusion Equation with Variable Coefficients[J]. Journal of Shenyang University: Natural Science, 2013,25(4):341-344.)

[6]Podlubny I. Fractional Differential Equations[M]. San Diego: Academic Press, 1999.

[7]金承日,潘友思. 时间分数阶色散方程的有限差分法[J]. 黑龙江大学自然科学学报, 2011,28(3):291-294.

(Jin Chengri, Pan Yousi. A Finite Difference Method for the Time Fractional Dispersive Equation[J]. Journal of Natural Science of Heilongjiang University, 2011,28(3):291-294.)

[8]马亮亮. 时间分数阶扩散方程的数值解法[J]. 数学的实践与认识, 2013,43(10):248-253.

(Ma Liangliang. A Numerical Method for the Time Fractional Order Dispersion Equation[J]. Mathematics in Practice and Theory, 2013,43(10):248-253.)