中短冷弯薄壁轴压构件承载力计算

周 乐, 王军伟, 聂晓梅

(1. 清华大学 土木工程系, 北京 100084; 2. 沈阳大学 a. 污染环境治理与区域生态安全重点实验室, b. 建筑工程学院, 辽宁 沈阳 110044)

近年来,随着我国经济建设的发展,我国建筑行业迅速发展,其中,钢结构在现代化建设中的地位正日益突出,在国民经济的各个领域均得到了大量应用[1].在建筑行业中,钢结构相比于其他结构形式,在使用方面有明显的优点,如:钢材相对于混凝土、砌体以及木材等材料强度高,自重轻,材质均匀,塑性、韧性好,工业化程度高等.在钢结构的发展过程中,钢材正在向高强度、延性以及韧性优越的方向发展[2].由于高强度钢材的出现,构件截面尺寸得到有效的缩减,由此在设计过程中使得薄壁类构件的应用越来越广泛.由于冷弯薄壁类构件相比于普通热轧类构件更能合理地发挥材料的力学性能,以达到节约材料等目的,其在今后的发展应用中将会逐渐替代热轧类构件在部分结构体系中的应用.

在冷弯薄壁类受压构件的研究中,对于长柱的研究,各国在规范计算方面得到了统一.由于长柱其最终极限状态为整体屈曲,一般根据欧拉临界应力计算即可.而对于中等级短柱的研究,则一直是各国学者关注的热点问题,其主要是因为中等级短柱的极限状态受局部屈曲或局部与整体相关屈曲的控制,而随着近几年来构件截面形式的复杂化,截面中还可能受到畸变屈曲的影响.

对于冷弯薄壁类构件的研究,各国已经取得了一定的研究成果[3-6].目前,各国对于薄壁类中长柱及短柱受压构件的计算,主要采用有效截面法和直接强度法这两种计算方法.我国学者何保康、周绪红及郭彦林等[4,7-9]分别采用有效截面法对C型、槽型以及卷边槽钢进行了分析计算,并取得了一定的研究成果,同时被我国《冷弯薄壁型钢结构技术规范》所采用.

在国外,直接强度法已被列入规范之中,如北美冷弯型钢结构技术规范NAS及美国规范AISI[10-12]等.但在我国,直接强度法是在近十年来为解决复杂类截面的局部屈曲、整体屈曲及畸变屈曲等一系列屈曲形式的计算问题而逐渐被应用的计算设计方法,尚未列入我国规范之中.随着直接强度法在我国实际应用的增多,这种计算方法加入计算规范中指日可待.本文以有效截面法和直接强度法为基础,以各国的钢结构计算规范为例,介绍并对比分析了有效截面法和直接强度法的适用范围,以及两种计算方法存在的弊端,并为钢结构设计中薄壁类受压构件的设计提供了参考依据.

1 有效截面法

1.1 薄壁柱承载力与柱长及宽厚比的关系

薄壁类受压构件是一类特殊的构件,其柱长与构件承载力的关系如图1所示.对于短柱而言,即图1中的阶段①,在此阶段,构件不受整体屈曲的影响,构件承载力只受截面局部屈曲应力和屈服应力的影响. 此阶段中,构件在极限状态下最大应力截面进入塑性阶段.对于中等长度构件,即图1中的阶段②,构件受局部屈曲、整体屈曲的影响或两者相关作用的屈曲的影响,在极限状态下,最大应力截面中应力可能处于弹性阶段或塑性阶段,其构件的承载力计算要分别考虑局部屈曲、整体屈曲以及两者的相关作用后才可以确定.对于长柱而言,对应于图1中的阶段③,在极限应力状态下,其截面应力处于弹性阶段,其构件承载力可直接由欧拉临界应力计算而得.

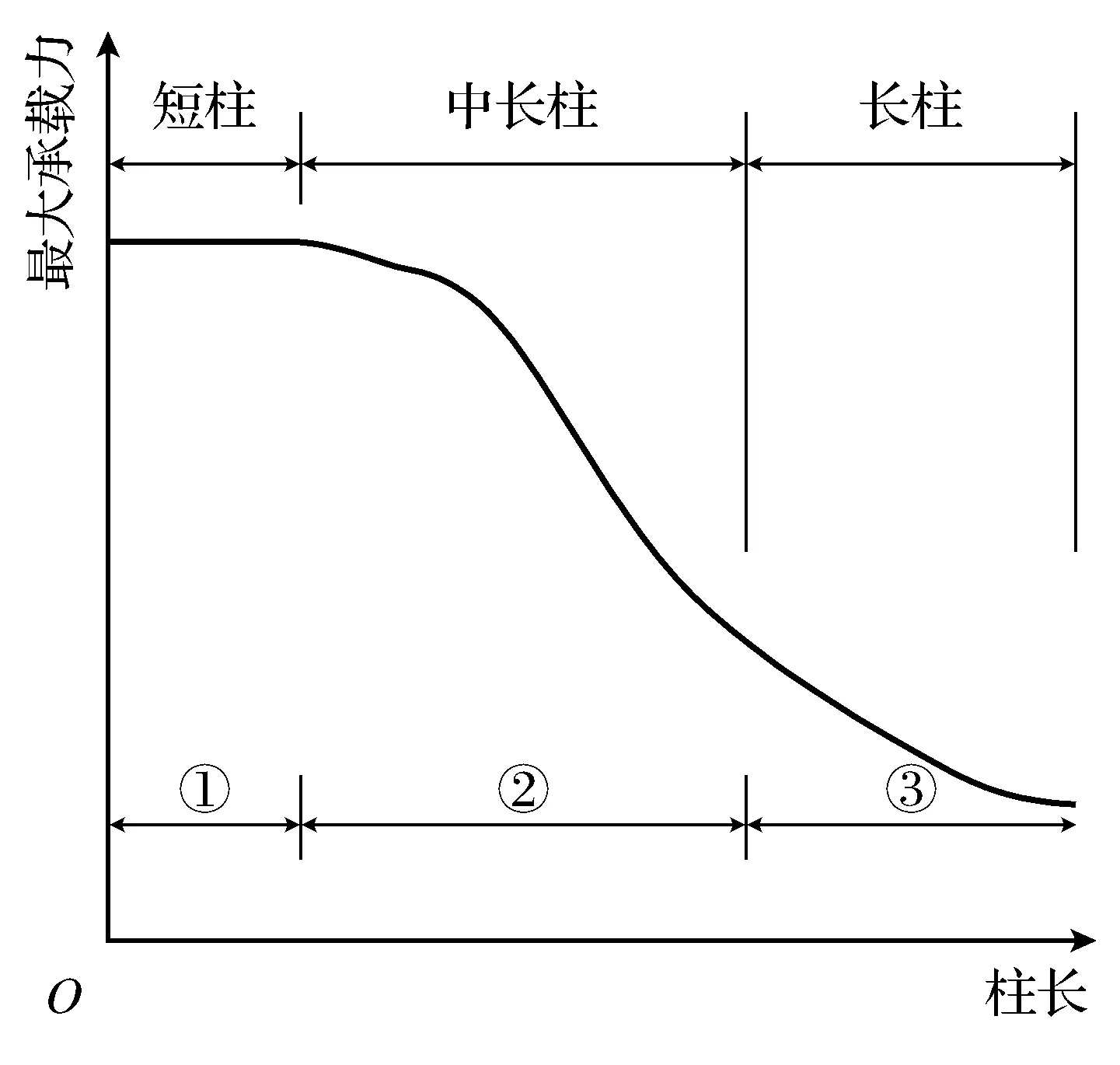
图1 构件承载力与柱长关系示意图Fig.1 Relationship map of component capacity and column length

图2为固定构件长度及板件厚度的受压板件截面承载力与板件宽厚比的关系示意图.规范中,一般规定板件的宽厚比,以限制构件部分板件的局部屈曲的出现,或以此限值为分界点,来考虑采用有效截面法和直接强度法计算折减后的构件承载力.图2中的第①阶段对应于图1中的阶段③,在拐点1之前,随着截面弯曲刚度的增加,截面极限承载力线性增加,整个阶段屈曲破坏模式呈现出整体屈曲的破坏模态;从拐点1过渡到拐点2,经历的阶段②对应于图1中的阶段②,在此阶段,截面承载力由局部屈曲控制逐渐过渡到由截面屈服承载力,在此阶段中,会有局部屈曲和整体屈曲相关作用的屈曲模态的出现;对于图2中的阶段③,其破坏形态主要受截面局部屈曲的控制,进入此阶段后,其屈曲破坏模态基本一致,其截面承载力的增加与截面宽度的增加呈线性增加的趋势.

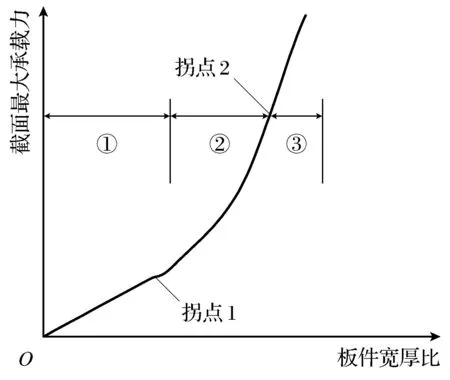
图2 截面承载力与板件宽厚比关系示意图(柱长、板件厚度为固定值)Fig.2 Relationship schematic of section bearing capacity and proportion of width and thickness

1.2 有效宽度法

有效宽度法起初应用于板件类构件的计算. 由于板件类构件的相对宽厚比较大,由板件的局部屈曲临界应力的计算公式可知,局部屈曲临界应力与宽厚比的平方成反比关系,因此,对于大宽厚比的构件而言,构件截面局部屈曲可能出现在整个截面屈服前,截面部分的屈曲导致整个截面的屈服承载力降低. 板件的屈曲示意图如图3所示.

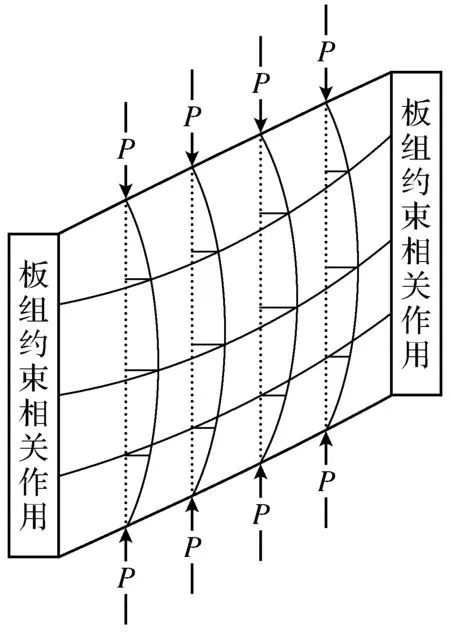
图3 板件屈曲示意图Fig.3 Schematic of plate buckling

为了计算这类截面的承载力,在20世纪30年代,Karman首次提出“有效宽度” 的概念[13],采用边缘最大应力代替整截面的平均应力,其截面应力分布及有效宽度分布如图4所示.其后,Winter又进行了相关的修正,形成了Winter有效截面计算公式,并被一些国家规范所采用,如欧洲大陆一些国家、加拿大、英国以及中国等.

根据图4可知,钢管截面应力分布呈现函数关系,但是针对于不同的截面形式,从图4中可以得到

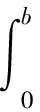
(1)

则

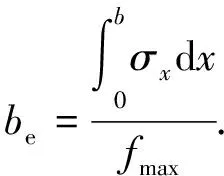
(2)

对于有效截面法,计算的关键在于有效宽度be的计算,Winter根据大量实验得到了有效宽度计算的半经验公式:

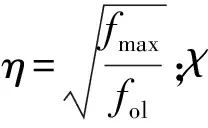
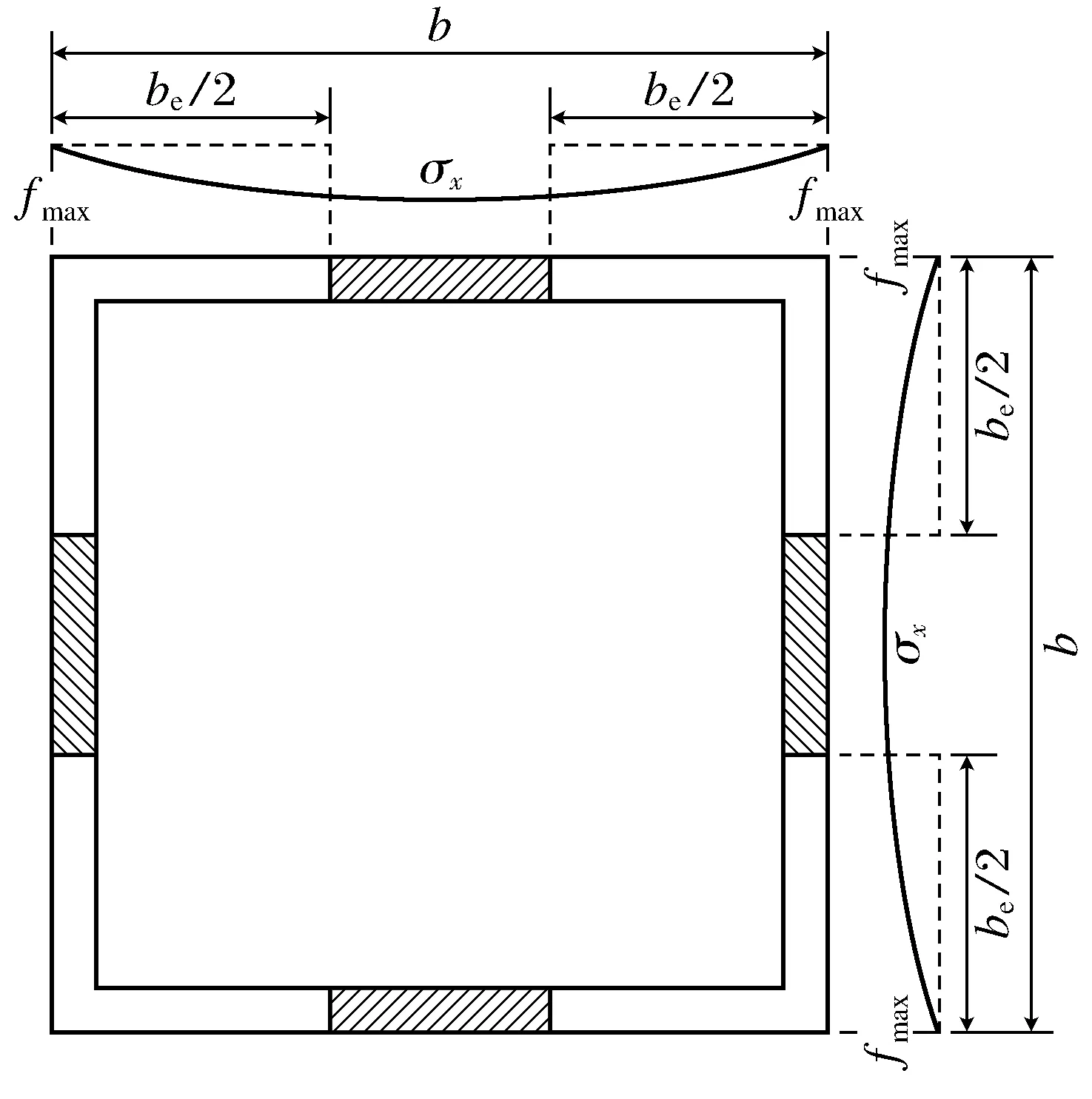
图4 有效截面及应力分布图Fig.4 Effective cross-section and stress distribution

1.2.1 AS 4100规范计算方法

冷弯管有效截面示意图如图5所示.

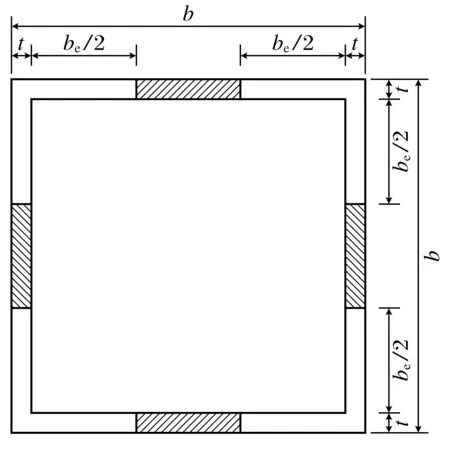
图5 冷弯管有效截面示意图Fig.5 Schematic diagram of effective cross-section of cold bending

根据AS 4100规范,截面设计计算承载力为

φNs=φκfAnfy.

(5)

式中,φ为承载力分项系数,取为0.9;Ns为截面名义承载力;κf为形状系数;An为净截面面积;fy为屈服强度.

对于SHS(方形管截面),截面形状系数κf为

在AS 4100中,长细比限值 (λey)为40,则

矩形管有效截面分布图如图6所示. 对于矩形截面,其计算分腹板和翼缘均不完全有效、腹板完全有效但翼缘部分有效、翼缘完全有效但腹板部分有效3种情况,其对于腹板和翼缘的截面有效宽度be的计算与方管的计算类似.

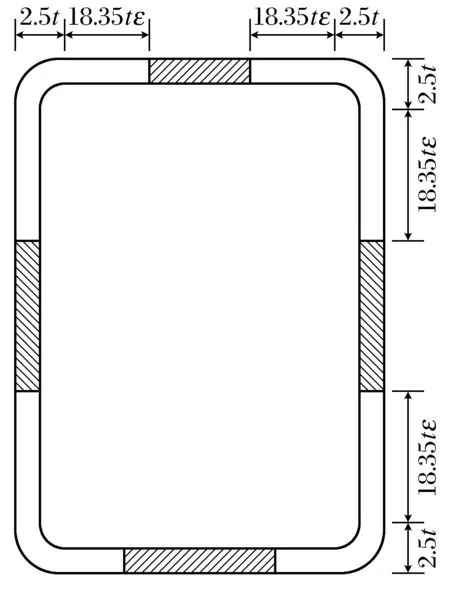
图6 矩形管有效截面分布图Fig.6 Distribution map of effective cross-section of rectangular tube

1.2.2 BS 5950 Part 1规范计算方法

在BS 5950 Part 1[11]规范中,截面的抗压承载力计算公式为

Pe=Aeff·pc.

(9)

式中,Pe为抗压承载力,Aeff为有效截面面积,pc为抗压强度.

在BS 5950 Part 1规范中,规定截面宽厚比的限值,当超过此限值时,即判定截面为不完全有效截面.

根据图6,当腹板和翼缘均不是完全有效时,有效截面面积的计算公式为

同理,可类似地推导出单个翼缘或腹板不是完全有效时的Aeff的计算公式:

2 直接强度法

直接强度法是继有效截面法之后又一计算截面屈曲承载力的一种新方法,其在北美钢结构规范中已经得到了应用.

对于轴心受压钢管而言,可以将其分为四个互相支撑的板组,即将钢管看作均匀受压板件,如图3所示.对于均匀受压板件而言,在板件截面上局部屈曲的出现,使得板件受压面上的应力分布如图4所示,采用直接强度法只需计算截面弹性局部屈曲临界应力fol(也称为有效应力)即可.

冷弯受压截面应力分布图如图7所示. 图7中,板件截面承载力的计算公式为

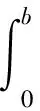
(12)

则

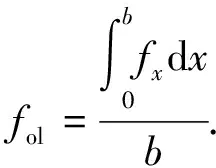
(13)

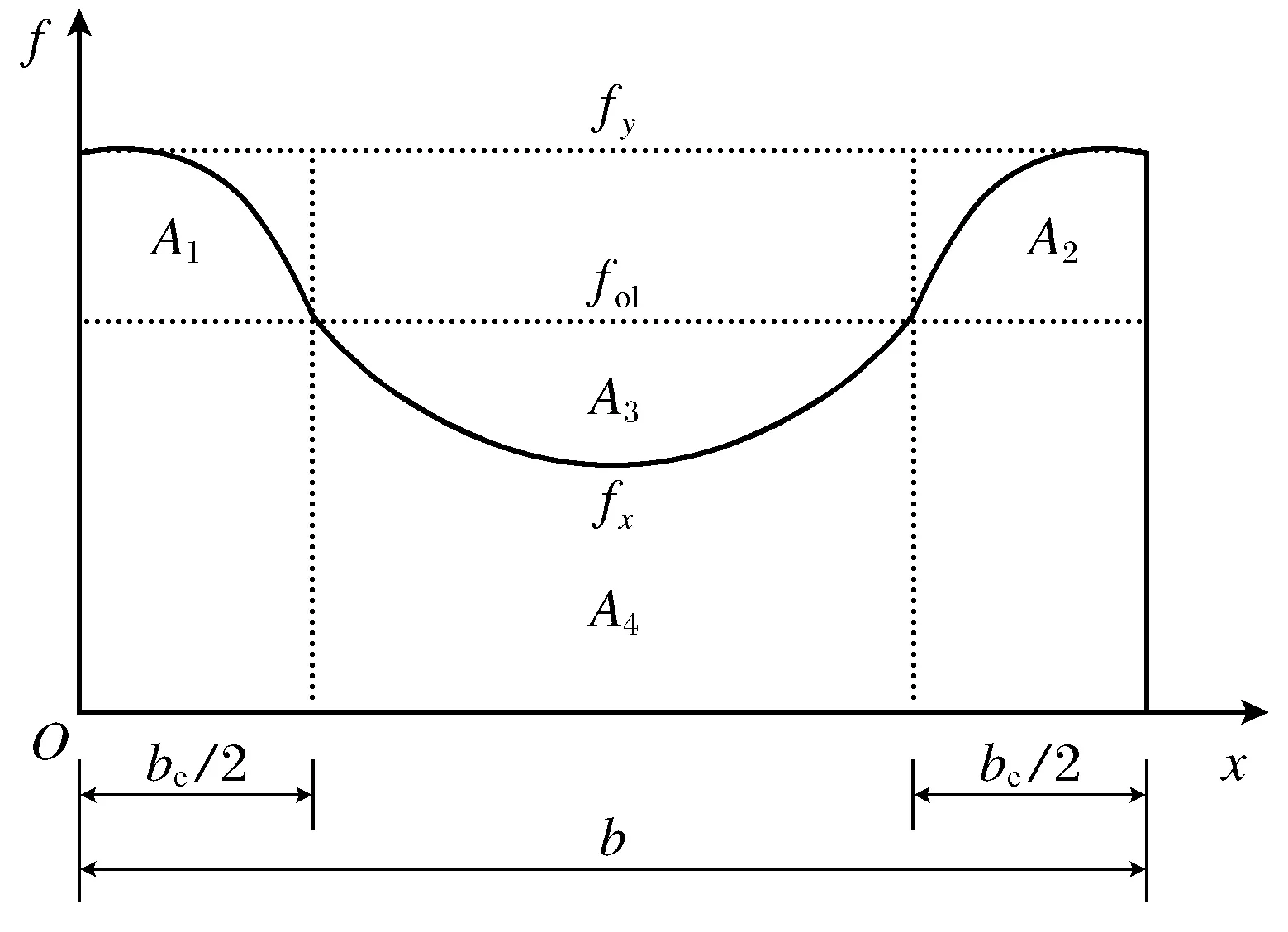
图7 冷弯受压截面应力分布图Fig.7 Stress distribution of cold-formed pressure-section

在北美规范NAS 2004[12]中,轴压构件承载力的计算公式如下.

(1) 考虑局部及整体屈曲的受压构件承载力:

当λl<0.776时

Pl=fmaxA;

(14)

当λl>0.776时

(15)

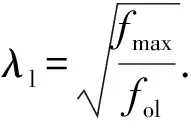
(2) 考虑畸变屈曲时的受压构件承载力:

当λlo<0.561时

Plo=fyA;

(16)

当λlo>0.561时

(17)

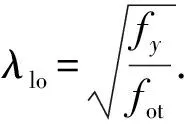
构件最终承载力为P=min{Pl,Plo}.

对于整截面弹性局部屈曲临界应力fol的计算,有解析法和数值法两种,其中,解析法适用于截面形式简单、规则的截面,同时,对于简单截面而言,截面的宽厚比变化后,计算公式就会有较大的变化,致使对于弹性临界局部屈曲应力的计算公式没有统一的计算形式.对于复杂的截面,如现在使用较多的卷边槽型、“Z”形截面等形式的弹性局部屈曲临界应力的解析形式的计算公式,目前的文献中还未出现.对于数值法,采用较多的为有限条计算程序CUFSM,如何保康、石宇等[7-8]在采用直接强度法计算冷弯构件截面弹性局部屈曲临界应力时,均采用有限条程序CUFSM[14]进行计算.但是,有限条软件有其很大的弊端,即其对构件的边界条件的约束只能为简支构件,同时,对于变截面构件,其不能进行建模计算.

综上分析可知:有效截面法削减的为构件的截面面积,而直接强度法削减的为构件的截面应力;有效截面法的计算重点为有效宽度或厚度的确定,直接强度法的重点为构件的截面弹性局部屈曲临界应力的计算;有效截面法中,有效宽度或厚度的计算均为采用试验或数值模拟计算进行回归得到的数据;直接强度法中,截面弹性局部屈曲临界应力的计算在简单截面的计算之中采用解析法、复杂的截面采用有限条法进行数值的近似计算.

直接强度法与有效截面法的区别是:直接强度法中,弹性局部屈曲临界应力fol是对应于整个截面的,即考虑了截面板组相关影响的整个截面的局部屈曲临界应力;而有效截面法计算的为单独板件的有效宽度,进而确定整个构件的承载力,因此,其对复杂截面的形式、板组相互作用较大的构件不适用于计算.

3 结 语

(1) 本文以各国钢结构设计规范为基础,介绍了对于轴压钢管短柱及中等长度柱由局部屈曲或局部屈曲与整体屈曲相关作用控制的构件的有效截面和直接强度计算方法.

(2) 有效截面法以板件计算为基础,不考虑或部分考虑板组之间的相关作用;直接强度法以整个计算截面为基础,板组之间的相关作用真实地反映在计算公式之内.

(3) 有效截面法适用于截面形式简单的构件的计算,对于复杂的截面形式,其不仅计算复杂,且精确程度难以保证.直接强度法在复杂计算中采用有限条程序CUFSM计算,可以方便地计算复杂的截面,但是对于构件边界条件及变截面形式的限制是有限条程序CUFSM广泛应用的前提.

(4) 针对有效截面法和直接强度法的弊端,今后在直接强度法的基础之上,针对截面弹性局部屈曲临界应力的计算,对于不同构件的边界约束条件、截面形式(如变截面)的数值计算是今后研究的重点及难点问题.

参考文献:

[ 1 ]刘声扬,王汝恒. 钢结构:原理与设计[M]. 2版. 武汉:武汉理工大学出版社, 2010.

(Liu Shengyang, Wang Ruheng. Steel Structure: Principle and Design[M]. 2nd ed. Wuhan: Wuhan University of Technology Press, 2010.)

[ 2 ]施刚,班慧勇,石永久,等. 高强度钢材钢结构研究进展综述[J]. 工程力学, 2013,30(1):1-13.

(Shi Gang, Ban Huiyong , Shi Yongjiu , et al. Overview of Research Progress for High Strength Steel Structures[J]. Engineering Mechanics, 2013,30(1):1-13.)

[ 3 ]中华人民共和国建设部. GB 50017—2003钢结构设计规范[S]. 北京:中国计划出版社, 2003.

(Ministry of Development of the People’s Republic of China. GB 50017—2003 Code for Design of Steel Structures[S]. Beijing: China Planning Press, 2003.)

[ 4 ]石宇,周绪红,苑小丽,等. 冷弯薄壁卷边槽钢组合工字梁极限承载力计算的有效宽度法[J]. 土木工程学报, 2011,44(6):8-17.

(Shi Yu, Zhou Xuhong, Yuan Xiaoli, et al. Effective Width Method for Load-carrying Capacity of Cold-formed Steel Composite I-beams[J]. China Civil Engineering Journal, 2011,44(6):8-17. )

[ 5 ]湖北省发展计划委员会. GB 50018—2002冷弯薄壁型钢结构技术规范[S]. 北京:中国计划出版社, 2002.

(Hubei Province Development and Planning Commission. GB 50018—2002 Technical Code of Cold-formed Thin-wall Steel Structures[S]. Beijing: China Planning Press, 2002.)

[ 6 ]清华大学土木工程系. CECS77∶96钢结构加固技术规范[S]. 北京:中国计划出版社, 2005.

(Department of Civil Engineering of Tsinghua University. CECS77∶96 Technical Specification for Strengthing Steel Structures[S]. Beijing: China Planning Press, 2005.)

[ 7 ]何保康,蒋路. 冷弯薄壁型钢构件的直接强度法[J]. 建筑结构, 2007,37(1):20-23.

(He Baokang, Jiang Lu. Direct Strength Method of Cold-formed Thin Wall Steel Members[J]. Building Structure, 2007,37(1):20-23.)

[ 8 ]石宇,周绪红,苑小丽,等. 冷弯薄壁卷边槽钢轴心受压构件承载力计算的折减强度法[J]. 建筑结构学报, 2010,31(9):78-86.

(Shi Yu, Zhou Xuhong, Yuan Xiaoli, et al. Strength-reduction Method for Load-carrying Capacity of Cold-formed Lipped Channel Columns under Axial Compression[J]. Journal of Building Structures, 2010,31(9):78-86. )

[ 9 ]郭彦林,张婀娜,江磊鑫. 卷边翼缘工形截面构件的局部稳定性能[J]. 工业建筑, 2009,39(9):1-6.

(Guo Yanlin, Zhang Enuo, Jiang Leixin. Research on Local Bucking of Lipped H-section Members[J]. Industrial Construction, 2009,39(9):1-6. )

[10]American Iron and Steel Institute. 1996 Edition of the Specification for the Design of Cold Formed Steel Structural Members[S]. Washington, 1997.

[11]British Standard Institution. BS 5950: Part 1, Structural Use of Steelwork in Building[S]. London, 1990.

[12]American Iron and Steel Institute. North American Specification for the Design of Cold-Formed Steel Structural Members:Appendix 1[S]. Washington, 2001.

[13]von Karman T,Sechler E E,Donnell L H. The Strength of Thin Plates in Compression[J]. Transactions of the American Society of Mechanical Engineers, 1932,54(2):53-57.

[14]Schafer B W. Elastic Buckling Analysis of Thin-Walled Structural Members by Finite Strip Analysis[M]. Baltimore: Johns Hopkins University, 2007.