基于排队论的车站售票系统优化与改善
2014-03-25张晓磊马从安
张晓磊, 马从安, 申 晨
(中国矿业大学 矿业工程学院,江苏 徐州 221008)
排队现象在社会生活中非常普遍,与人们的生活息息相关。火车站排队进行购票,公交车站台上排队等候上车,餐厅里排队进行买饭等等。伴随着我国铁路客运发展越来越快以及改革力度的不断深化,火车站排队购票现象日益成为社会关注的焦点。石家庄站于2012年12月21日正式通车运营,成为京广高铁、石太高铁、石德铁路的重要枢纽中心,是促进石家庄乃至华北地区经济发展的强大动力。由于第一年运营,客流量巨大,出现因窗口开放少、服务效率低而导致旅客等待时间长的排队现象,影响了旅客出行的效率,降低了旅客对铁路服务的满意度;然而开设过多窗口,又会增加铁路的自身成本,造成资源的闲置浪费。2013年3月10日,我国撤销铁道部,实行铁路政企分开。铁路部门必须加强自身的机构改革,从提高旅客的满意度出发,在满足旅客多样化需求的前提下,开设适当窗口,从根本上解决春运购票难的问题,提高资源的利用率,增强自身的竞争力。
目前,有很多春运期间铁路客运紧张的文献报道。针对这类现象,已有一些关于铁路系统改善的研究成果。李季涛[1]等运用排队理论建立了基于可接受等待时间的非客运高峰时期的售票窗口数目优化模型,有利于提高售票系统的动态管理。陈磊[2]等通过对排队系统的分析模拟,证明了客运高峰期增设人工窗口的必要性。纪莹[3]等依据供需均衡理论,通过模型分析得出了车站在非客运高峰时期全天不同时段适宜服务的窗口需求数。宋卫斌[4]等探讨了具有优先权的多级顾客服务(M/M/C)排队模型,提出从成本和效率来解决排队系统的优化问题。然而,上述文献没有提出车站在客运高峰时期的合适窗口数目,春运等客运高峰期不但涉及到广大旅客的安全便捷出行,更考验着铁路部门的综合服务能力。
在铁路客运高速发展、旅客需求复杂多样和改革深化的大背景下,对石家庄站2013年春运期间的客运情况进行调查,应用排队理论和工业工程思想对问题进行分析研究,并利用计算机软件进行模拟运算,提出车站增设窗口的具体数目以及一些改进措施,以增强石家庄站的客运能力,降低车站的运营成本,提高旅客的满意度和服务质量,对客运高峰时期的准备工作有借鉴意义。
一、售票服务窗口排队系统组成
火车站售票服务排队系统是一个典型的随机排队系统[5-6],它的服务实体为出行购票的旅客,服务主体为售票窗口。其特征描述如下:
(一)输入过程
在售票排队系统中,客流量比较大,因此可以认为旅客来源是无限的。单位时间进入系统的旅客流属于简单流,并且旅客到达的时间间隔相互独立。因此,可以得到单位时间内进入系统的顾客数服从参数为λ的泊松分布,λ表示系统的平均到达率,顾客到来的时间间隔服从期望为1/λ的负指数分布。
(二)排队规则
售票窗口的服务规则一般是先到先服务。在春运这样的客流高峰期,旅客们的回家心切,前来购票的旅客大都会选择排队购票而不放弃离开,因此该系统的排队规则可认为是等待制。另外,当前的火车站售票大厅的空间都比较宽敞,不需要限定系统容纳的最大顾客人数,所以认为系统能够容纳的旅客数是无限制的。旅客进入大厅后,根据队列人数最少的原则进行排队购票。
(三)服务时间
火车站设置多个售票台为旅客提供服务,售票台之间是并联关系。每个窗口的服务时间相互独立并服从参数为μ的负指数分布,其期望值为1/μ。1/μ表示单个旅客的平均服务时间,而μ表示售票排队系统的平均服务率,即单位时间内平均服务的旅客数。根据以上描述,火车站售票服务系统可表示为(M/M/C/∞/∞/FCFS)模型,即顾客来源和系统容量是无限的,旅客进入系统的时间间隔服从负指数分布,售票窗口的服务时间服从负指数分布,系统设置C个并联的服务窗口,遵循先到先服务的规则。简化的火车站售票服务系统模型如图1。
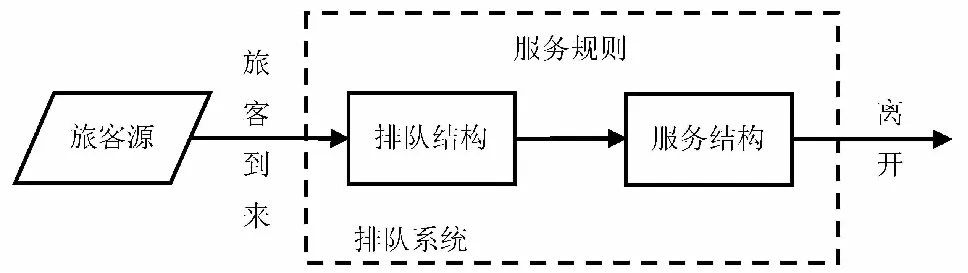
图1 排队系统结构图
二、售票窗口排队系统的主要指标
研究售票服务排队系统的主要目的是通过描述系统的运行状况,对系统进行控制和改善,提高系统的综合服务质量和整体效率,使系统的运行状态处于最佳。而描述系统,需要合适的数量指标,售票服务系统的主要数量指标如下:
(一)队列长Lq和队长Ls
队列长是指系统中正在排队等待服务的平均旅客数,其期望值记为Lq。
队长是指系统中的平均购票旅客数(排队等待的旅客数与正在接受服务的旅客数之和),其期望值记为Ls。
(二)等待时间Wq和逗留时间Ws
等待时间[7-8]是指从旅客到达系统的时刻延续至开始接受服务时的时刻的这段时间,其期望值记为Wq;逗留时间是指从旅客到达系统的时刻延续至接受完服务的时刻的这段时间,其期望值记为Ws,这两者都是随机变量。
(三)忙期(服务强度)ρ
忙期是指从旅客到达空闲着的售票系统起,到售票系统再次成为空闲止的这段时间,记为ρ。它刻画了售票系统的繁忙程度。ρ太大,说明服务人员总是处于忙碌之中,容易疲劳而导致效率低下;ρ太小,可能导致排队队伍越来越长而降低旅客的满意度。在(M/M/C/∞/∞/FCFS)模型中,令ρ=λ/Cμ为整个系统的服务强度或平均利用率[9]。其中,λ为系统的平均到达率,μ为单个服务台的平均服务率,Cμ为整个系统的平均服务率。
当售票系统处于比较稳定的状态时,稳态概率的关系式可以表示为:
(1)
又
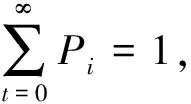
(2)
故初始概率:
(3)
于是系统的运行指标如下:
队列长
(4)
队长
(4)
逗留时间
(6)
排队时间
(7)
三、车站售票服务排队系统模型分析
(一)石家庄站及客流状况
2013年春运持续40天,石家庄站在春运期间迎送旅客240万人次,占全国铁路春运客运量2.2亿人次的1%。客运最高峰出现在节前一周的2月7日,客流量将近8万人次。
当时石家庄站共开通了3个售票处,分别为:位于火车站一层售票大厅的第二售票处,设有18个人工窗口,20台自助售票机和取票机;位于二层候车大厅南北两侧的第五售票处和第六售票处,设有12个人工窗口和10台自助售票机;位于地下出站口的第八售票处,设有2个人工窗口以及5台自助售票机。共有32个人工售票窗口,35台自助售票机和取票机,共计67个服务台。春运期间,这67个服务台均开通,以便为旅客提供方便。
(二)数据统计分析
春运是火车站售票最繁忙、最特殊的时期,2013年春运期间石家庄站平均日运送旅客6万人次,为缓解客流量带来的压力,石家庄站新增34对、68列临客,以方便旅客的出行。
1.非客运高峰日
通过实地调查,测定春运期间客流量相对平缓情况下某天5个时间段的旅客进厅和购票情况,如表1和表2:

表1 旅客进厅购票人数

表2 售票台服务人数
根据表1,可计算出:春运期间客流量相对平缓情况下旅客平均到达率λ≈2 500人/h,约41.67人/min;此情况下旅客到达平均时间间隔为0.024 min/人;根据表2,可计算出:每个售票台的平均服务率μ=38.6人/h,约0.64人/min;此情况下旅客的平均服务时间为1.57 min/人。整个系统的平均服务率ρ= 0.971 8。
通过调查资料,了解到售票厅每个服务台单位时间的服务费用约为35元/h(包括售票员工资、管理费用以及设备折旧费等);旅客在系统内单位时间的逗留费用约为15元/h(考虑旅客的平均工资、路费以及餐饮费等);由于多种原因旅客购票失败或不满离开而造成车站的机会成本约为20元/h。旅客排队过程中可接受的等待时间约为10 min,队伍长度约为20人。排队时间超过20 min,旅客会产生烦躁心情,超过30 min,旅客对车站服务质量的满意度急剧下降。借助Win QSB软件运算结果及敏感性分析见表3。
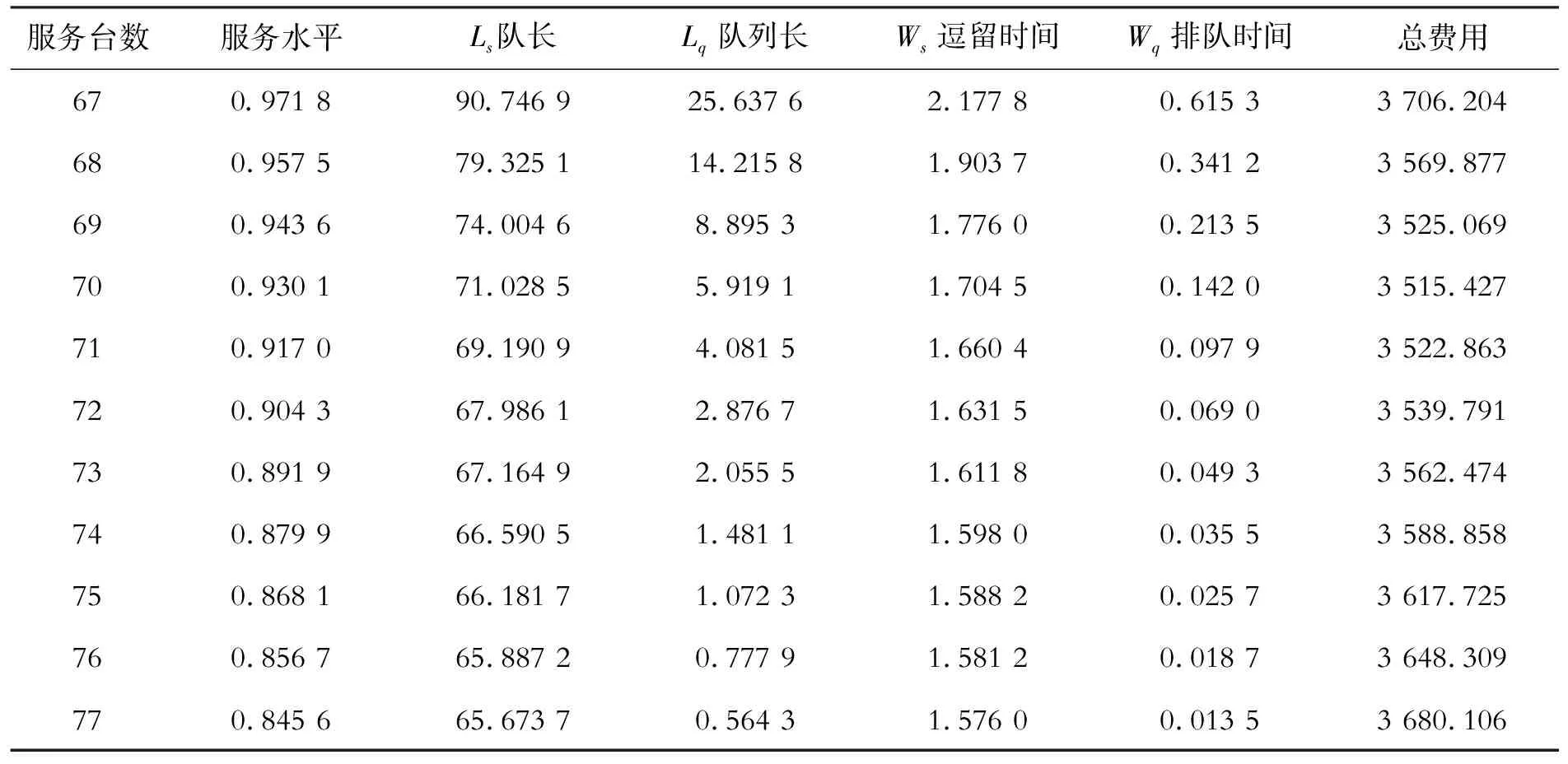
表3 客流量平缓时运算结果及敏感性分析
从表3可以看到,春运期间,在客流量相对平缓的情况下,开通67个服务台的队列长为25.637 6人,旅客的平均等待时间为36.92 min,服务强度为97.18%,系统运行状态比较紧张。因此综合考虑车站的成本费用、旅客的可接受等待时间和队伍长度等服务水平因素[10-11],可以确定在客流量相对平缓的情况下,开通70个售票台,是比较合适的。此时队伍长度约为6人,旅客排队时间为8.52 min,服务强度为93.01%。
2.客运高峰日
2013年2月7日,石家庄站迎来春运期间客运最高峰,迎送旅客将近8万人次,通过实地调查,高峰日的平均到达率λ约为56 人/min,假设单个售票台的平均服务率μ不变,仍为0.64 人/min。借助QSB运算结果及敏感性分析见表4。
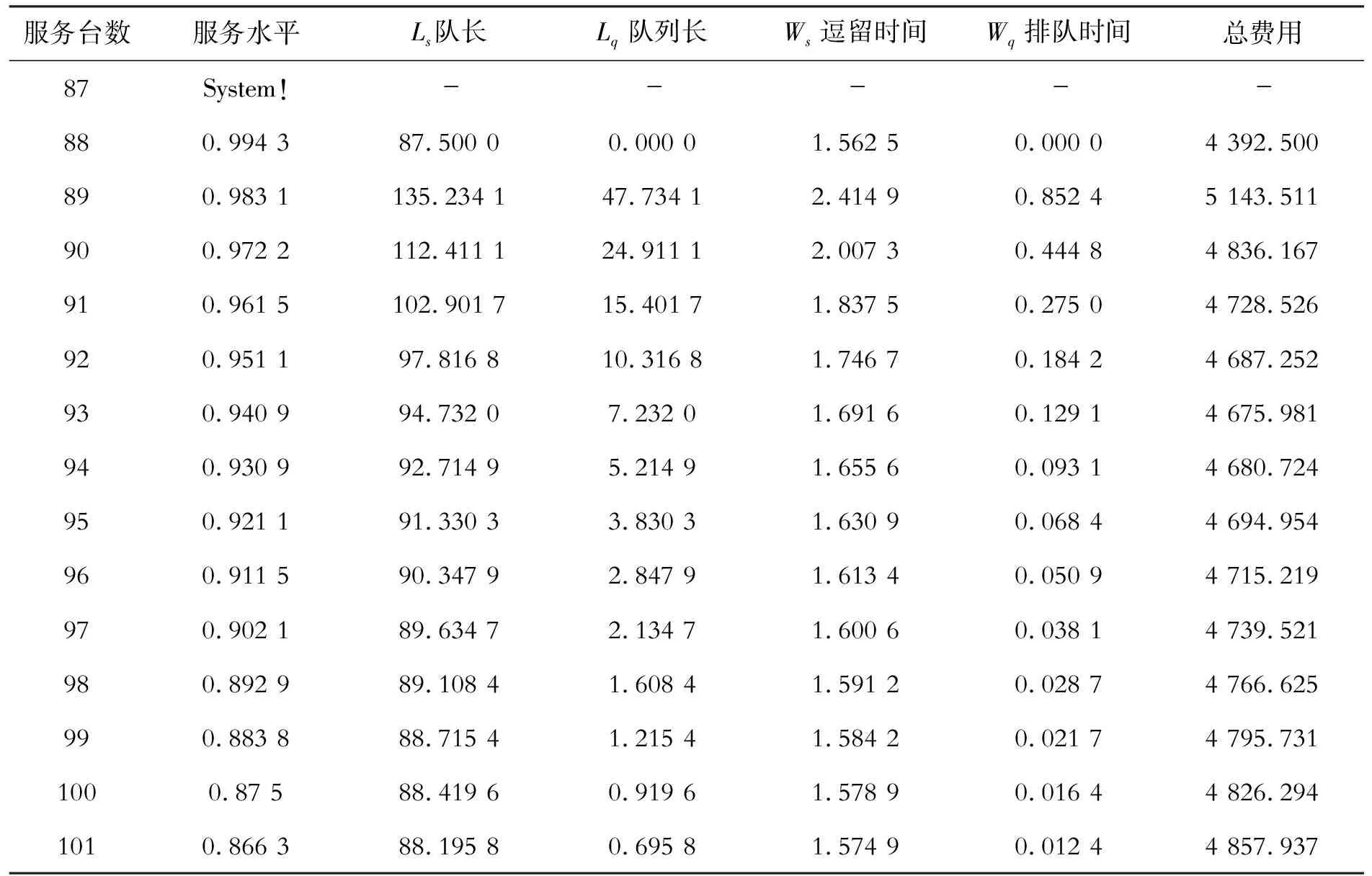
表4 客流高峰日的运算结果及敏感性分析
从表4可以看出,在客流高峰日,开通的售票台少于88个时,整个系统的服务强度ρ=1.006>1,排队会无限长。所以,至少应开通88个售票口。当然,开通售票台越多,越能满足旅客需求,但同时车站的自身成本也会增加。因此,结合车站的成本费用、旅客的可接受等待时间和队伍长度等因素,可以确定在春运的高峰日,开通93个售票台,比较合理。也就是说车站在全部开通已有售票台的基础上,再增开26个售票台。此时队伍长度为7.232人,排队等待时间为7.75 min,服务强度为94.09%。
(三)改善措施
以上分析可以看出,增开售票台数目,在很大程度上能够缓解车站售票系统的应对压力。但这仅仅属于提高车站的硬件服务能力,要真正增强车站的综合竞争力,还必须同时增强车站的软服务能力。通过调查发现,在整个售票服务过程中存在许多不合理的现象:
(1)旅客排队购票时售票窗口前方的旋转闸机会延长旅客上前寻求服务的时间。由于旋转闸机的存在,前一个旅客接受完服务并完全走过闸机后,后一个旅客才能走上前去寻求服务,而闸机位置离服务窗口有1米之远。因此,闸机的设置形式不太合理。
(2)售票人员是服务过程的主体之一,其服务效率直接决定着服务时间的长短进而决定服务率的大小。服务过程中,工作人员要根据旅客的需求在电脑上查询出列车信息,接受付费,拿出车票再递给旅客。调查发现,出票口离会话窗口比较远,胳膊的工作范围较大,影响服务效率。
(3)对于自助售、取票机的使用,有不少旅客还不清楚,仍然存在不少旅客坚持排长队到人工窗口而不去自助售、取票机前接受服务的现象。
上面几个因素,严重影响车站售票的服务效率,同时也可能引起旅客对售票工作的不满,从工业工程的角度来看,这是非常不可取的。基于以上因素,给出改进建议:
(1)旋转闸机应设在离窗口较远处的相邻着队伍的通道位置或者撤销掉旋转闸机的设置。
(2)将出票设备与钱匣子安置于会话窗口附近的服务人员旁边,缩小服务人员的工作范围,尽量只移动小臂,减少大臂的移动次数和范围。提高服务人员座椅的高度,使服务人员面对旅客呈现略微俯视而非仰视的姿势,因为仰视状态下,服务人员需要略举胳膊将车票和找零递给旅客,而俯视状态下,只需移动小臂就可以实现交易。
(3)在春运期间,车站应安排一些志愿者对自助售、取票机的使用进行指引服务,增强旅客的认识度,尽快减少因旅客不了解或者不会使用自助机而造成排队长的现象,分流站内窗口售票的压力;将售票厅的基本揭示语和标示统一规范、配备齐全,保证窗口电子屏运行良好,内容显示正确无误;规范售票时间,保证站内24 h不间断售票、退票、改签作业,售票人员就餐时增设一小时专窗,中途离开不应超过15 min;设置残疾人员及其他重点旅客专窗,做到标示明显、规格标准,同时根据不同时段的需要及时增设农民工、学生、军人、团体旅客等专窗,满足不同层次旅客的需求[12-13]。
四、改善分析评价
以上对售票流程和售票厅进行了合理地规划和改善,改善效果可以对售票和管理效率有较大程度的提高。售票厅管理工作的规划可以减少旅客排队的冗长混乱;售票流程的改善能够简化以下动作和时间:前面旅客服务完走过闸机门才轮到下一旅客上前的耽搁时间、售票员伸大臂取票的动作、售票员侧转身体并换手动作、售票员举胳膊放胳膊的动作。运用工业工程的模特法[14]对改善后的售票流程可表示为:8W5、M4G1M4P0、M4、M4P2M4P0。于是所节省的时间为8.13 s。这样单个售票台的平均服务率可由0.64人/min,提高到0.7人/min。借助Win QSB运算分析如下:
改善后,春运期间客流量相对平缓的情况见表5(λ=41.67人/min,μ=0.7人/min)。
改善后,春运期间客流高峰日的情况,见表6(λ=56人/min,μ=0.7人/min)。
从表5和表6中可以看出,经过改善购票流程,单个售票台的服务率提高到0.7人/min时,售票效率有显著的提高。
在春运客流量平缓的情况下,开设64个售票台就可以在较低的成本基础上满足旅客的需求了,比改善前少开6个售票台,成本较少约290元。此时队伍长度为6.16人,旅客排队时间为8.87 min。

表5 改善后客流量平缓时的运算结果及敏感性分析
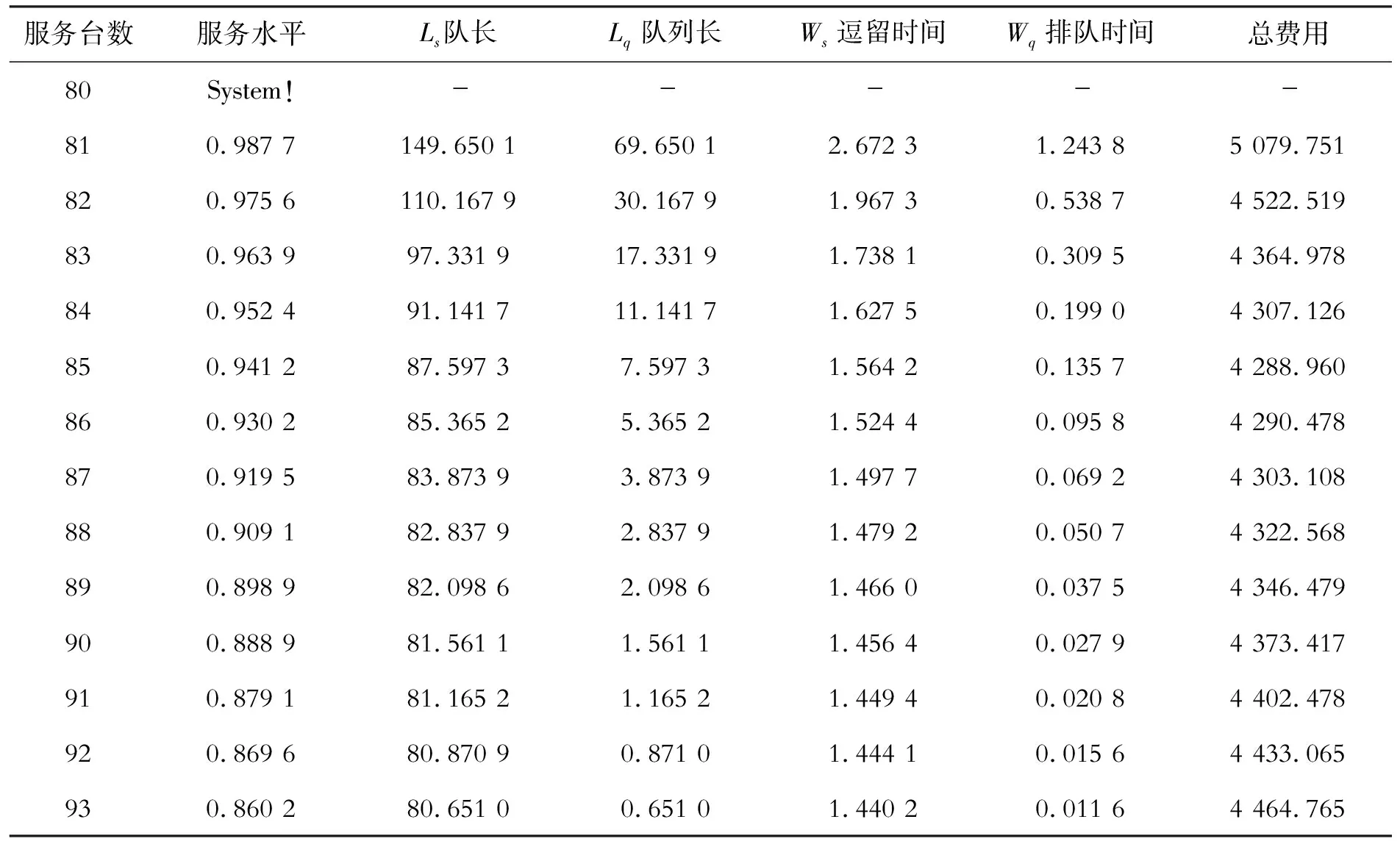
表6 改善后客流高峰日的运算结果及敏感性分析
在春运客流高峰日的情况下,开设85个售票台就能够满足需求,比改善前少开8个售票台,成本较少387元。此时队伍长度为7.6人,旅客排队时间为8.14 min。通过改善,维持了改善前的服务率(93.01%和94.09%),满足了旅客需求,同时还节约了成本,增强了车站的整体竞争力。
五、结语
本文从满足旅客的实际需求[15]出发,运用排队理论和工业工程思想,借助计算机的模拟运算,对车站售票和管理工作进行改善。通过数据分析表明,优化结果可以提高服务效率和顾客满意度,对优化车站资源、增强铁路部门的综合实力也有一定的指导作用。当然,由于铁路客运的复杂性和规模性,模型不能很准确地给出具体量化指标。铁路部门可以根据实际情况,进行动态的调整,为以后春运安全高效地运行提供参考。
参考文献:
[1]李季涛,杨俊锋,付佳.铁路车站售票窗口排队系统模拟优化[J]. 铁道运输与经济,2007,29(12):67-70.
[2]陈磊,王鹏,董静宜.基于排队论的火车站售票排队系统的分析与研究[J]. 成都信息工程学院学报,2010, 25(6):584-587.
[3]纪莹,徐行方.基于排队论的售票厅售票组织优化[J]. 交通与运输,2008(2):134-137.
[4]宋卫斌,苏秦.虚拟顾客服务系统排队模型[J]. 管理科学学报,2001,4(3):52-57.
[5]王硕,杨彦军.环渤海地区航空与铁路交互模式服务系统分析[J]. 石家庄铁道大学学报:自然科学版,2011,24(2):79-82.
[6]GUO P F,PAUL Z.The effects of the availability of waiting-time information on a banking queue[J]. European Journal of Operational Research,2009,198(5):199-209.
[7]陈胜波,何世伟,何必胜.基于免疫克隆选择算法的市域快速轨道交通列车开行方案优化研究[J]. 石家庄铁道大学学报:自然科学版,2013,26(3):81-86.
[8]高斯博.银行排队问题及窗口设置优化研究[J]. 北方经济,2011(7):80-81.
[9]《运筹学》教材编写组编.运筹学[M]. 3版.北京:清华大学出版社,2005:324-325.
[10]吴景龙,马毅.基于未确知测度理论的普通铁路客运站服务水平综合评价[J]. 石家庄铁道大学学报:自然科学版,2011,24(3):75-78.
[11]王健,胡碧琴.基于排队论的港口泊位服务系统优化仿真研究[J]. 物流科技,2011(7):31-35.
[12]李金棉.基于模糊聚类的高速公路运营成本预测[J]. 石家庄铁道大学学报:社会科学版,2012,6(2):18-20,26.
[13]CANONACO P, LEGATO P, MAZZA R M, et al.A queuing network model for the management of berth crane operations[J].Computers & Operations Research,2008,35(8):2432-2446.
[14]易树平,郭伏.基础工业工程[M]. 北京:机械工业出版社,2007:277-279.
[15]李华,牟瑞芳.基于灰理论的成都市铁路旅客周转量预测[J]. 石家庄铁道大学学报:自然科学版,2011,24(2):70-73.
