A Multi-model Approach for Soft Sensor Development Based on Feature Extraction Using Weighted Kernel Fisher Criterion*

(吕业)(杨慧中)**

Key Laboratory of Advanced Process Control for Light Industry of Jiangnan University, Wuxi 214122, China

A Multi-model Approach for Soft Sensor Development Based on Feature Extraction Using Weighted Kernel Fisher Criterion*

LÜ Ye(吕业)and YANG Huizhong(杨慧中)**

Key Laboratory of Advanced Process Control for Light Industry of Jiangnan University, Wuxi 214122, China

Multi-model approach can significantly improve the prediction performance of soft sensors in the process with multiple operational conditions. However, traditional clustering algorithms may result in overlapping phenomenon in subclasses, so that edge classes and outliers cannot be effectively dealt with and the modeling result is not satisfactory. In order to solve these problems, a new feature extraction method based on weighted kernel Fisher criterion is presented to improve the clustering accuracy, in which feature mapping is adopted to bring the edge classes and outliers closer to other normal subclasses. Furthermore, the classified data are used to develop a multiple model based on support vector machine. The proposed method is applied to a bisphenol A production process for prediction of the quality index. The simulation results demonstrate its ability in improving the data classification and the prediction performance of the soft sensor.

feature extraction, weighted kernel Fisher criterion, classification, soft sensor

1 INTRODUCTION

Petrochemical process is a typical continuous industrial process which is multivariable, nonlinear and uncertain in nature. The process operational data is featured with multi-modes, high disturbance and time-dependent dynamics [1]. Therefore, using a single model to describe a process may result in poor prediction performance and generalization ability [2, 3]. A multi-model approach with object properties considered can solve such problems. Unfortunately, traditional clustering algorithms may lead to overlapping phenomenon in subclasses so that edge classes and outliers cannot be effectively handled. Linear discriminant analysis (LDA) enables different subclasses to have maximum discriminant by searching for an optimal projection vector. This technology is mainly applied to image processing and face recognition for improving classification accuracy [4-8]. Kernel Fisher discriminant analysis (KFDA) is a nonlinear extension of LDA, which is more efficient in solution of nonlinear classification problems [9-14]. However, due to the structural limitation of KFDA, i.e., the definition of between-class scatter matrix is less than optimal, it is still difficult to accurately classify the data when edge classes and outliers coexist [15].

In order to further improve the prediction performance of the multi-model based on traditional clustering methods, a multi-model approach based on feature extraction using weighted kernel Fisher discriminant analysis (WKFDA) is introduced in this paper. First of all, based on the Fisher criterion, a new weighted function with variable weight is proposed to rectify the within-class scatter matrix and between-class scatter matrix. Secondly, the category information measurement is put forward to describe the scatter degree of within-class and between-class for each dimensional component. This index is applied to determine the number of feature vectors that should be included in the optimal projection matrix. Furthermore, the original data is successfully classified into multiple sub-classes based on the extracted projection feature. Then, the support vector machine (SVM) is employed to establish the sub-models using all the samples belonging to that sub-class [16-20]. Finally, a multi-model based soft sensor is obtained by using a switcher to combine the SVM sub-models. The proposed method is evaluated on a bisphenol A production process to indicate the real-time phenol composition at the dissolution tank outlet of a crystallization unit. The simulation results demonstrate the effectiveness of the proposed method.

2 WEIGHTED KERNEL FISHER DISCRIMINANT ANALYSIS

2.1 Kernel Fisher criterion

LDA searches for an optimal discriminant vector in a lower-dimension feature space to maximize the ratio of between-class scatter matrix over the withinclass scatter matrix. After projection of the original high dimensional data to the feature space, it becomes much easier to classify because the samples belonging to different sub-classes are more clearly separated, while the samples within-class are more compact.

Assume X is an n-dimensional data set which consists of N samples. It can be divided into C sub-classes, represented by Xi( i= 1,2,… ,C), which is composed of Nisamples. The between-class scatter matrix Sband the within-class scatter matrix Sωare given by [21, 22]

where m0is the overall mean of X, miand Piare the mean and prior probability of the subclass Xi, respectively.

The objective function based on Fisher criterion can be expressed as

where woptcan be obtained by solving a generalized eigenproblem specified by

and λ is a generalized eigenvalue.

KFDA can extract diagnostic characteristics through mapping the original data into a high-dimensional feature space, in which the diagnostic characteristics are essentially nonlinear discriminant features in the original data space. Similar to SVM and kernel principle component analysis (KPCA), KFDA also adopts the kernel trick [23]. Its basic idea is to project an original dataset X into a high-dimensional feature space F using a nonlinear mapping f, F:χ®f(χ). The input space is implied to give a strong nonlinear discriminant with the linear discriminant so that each category is separable. Suppose the mean value of the total samples is zero after projection, the objective function based on Fisher criterion is modified to

where the between-class scatter matrix is

and the within-class scatter matrix is

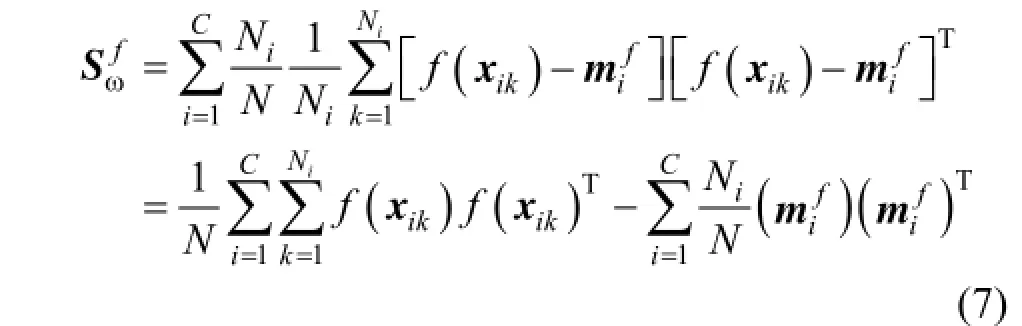
where

is the mean value of the ith sub-class. Because mapping into the high-dimensional space will lead to increased computational complexity, an inner product kernel function is introduced for implicit calculation so as to extract the feature in the high-dimensional space. The inner product kernel function is defined as

According to reproducing kernel theory, the solution of F space can be obtained by the samples in F space. Therefore, wfcan be determined by

where αl( l= 1,2,… ,N) is the corresponding coefficients.

Using the inner product to replace the kernel function, we have

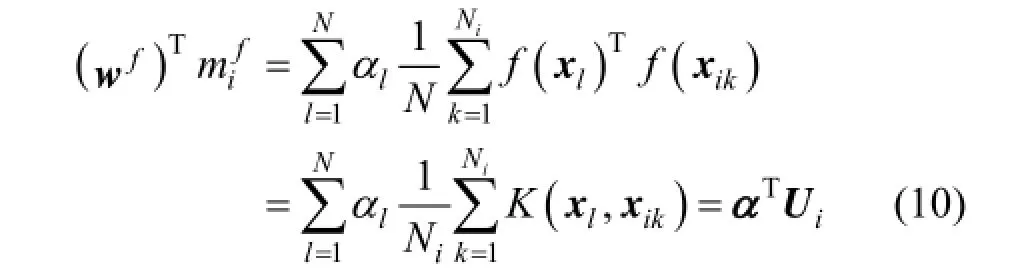
where

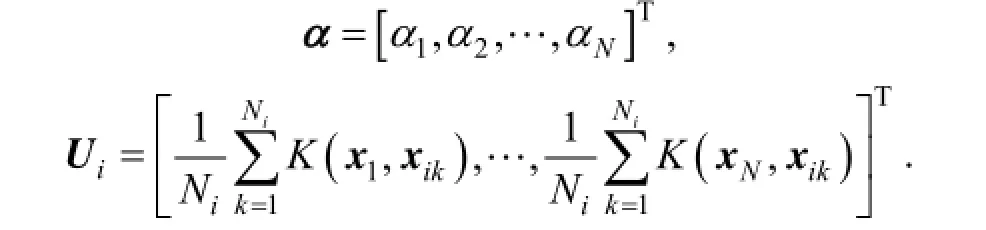
Using Eqs. (6) and (10), the following equation can be obtained

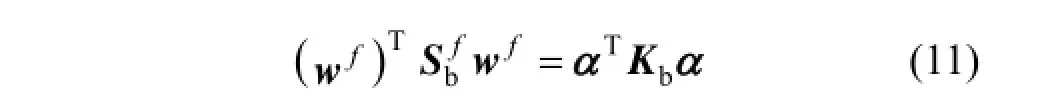
where Kbis calculated by

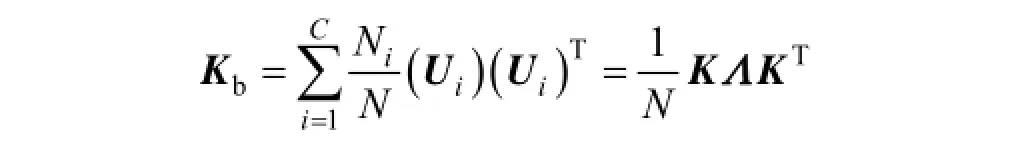
and K is an N×N kernel function matrix from a kernel mapping and Λ = diag (Λi)i=1,2,…,Cis a N×N block diagonal matrix and each element in the matrix is 1/Ni.

Since

combining Eqs. (9), (10) and (12) yields

where Kω= (KKT−KΛKT)/N .

The Fisher linear discriminant in F can be obtained through maximizingThe solution can be obtained by solving the eigenvector of λ Kωα=Kbα .

2.2 Improved algorithm of KFDA

The definition of between-class scatter matrix is less than optimal based on traditional Fisher criteria. According to Eq. (1), calculating the distance between the mean of the total mapped samples and the mean of the ith sub-class mapped samples, each subclass may easily deviate from the center of the mapped sample set and resulte in sub-classes overlap. Hence, the between-class scatter matrix in Eq. (1) is redefined by calculating the distances between each subclass as

Considering the example shown in Fig. 1, the sub-class 3 is defined as an edge class if it is far away from the sub-class 1 and sub-class 2. The projection axis A shown in Fig. 1 is obtained based on traditional feature extraction method. Apparently, because the edge sub-class 3 is excessively emphasized by its maximization between-class distance, the adjacent sub-classes overlap is resulted, as the case of subclasses 1 and 2 in Fig. 1.

Figure 1 Different projection axes of different definition of Sb

Accordingly, the between-class scatter matrix and the within-class scatter matrix are redefined to

where W(Δij) and W(Δik) are the weighted functions for between-class and within-class scatter, respectively.

The weighted scatter matrices of within-class and between-class defined in Eqs. (16) and (17) can decrease effectively the impacts of edge classes and outliers. Projection axis B is obtained by the modified scatter matrices, which has better discrimination ability than projection axis A. Similarly, the nonlinear form for the novel method is further derived using Eqs. (16) and (10). We have

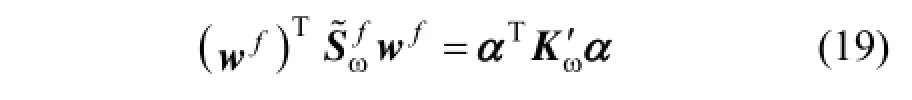
A Gaussian radial basis function is used as the inner kernel product function, defined as

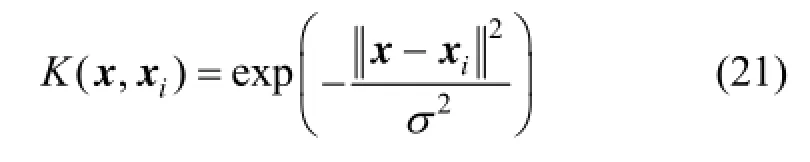
This function is widely used for its good learning ability. Furthermore, since the corresponding eigenspace is infinite, the finite sampled data must be linearly separable in this eigenspace. The weighted function is similarly defined as

The weight is transformed by the same nonlinear transformation of the sampled data. Therefore, it can reflect the weighted relationship of the sampled data in the feature space.

2.3 Category information measure and kernel parameters selection

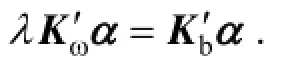
Generally, d is artificially determined. The larger d is, the more information is contained. But for the classification, remaining valid category information is the most important. After eigen transformation of the original data, the aggregation degree of the withinclasses and the dispersion degree of the betweenclasses can be evaluated by its each dimension.

The aggregation degree of the within-classes for the kth dimensional component can be described as

The dispersion degree of the between-classes for the kth dimensional component can be described as

where mikand mjkare the mean value of the kth dimensional component in the ith class and the jth class, respectively.

Combining Eqs. (23) and (24), an evaluation index is presented by the category information measurement, and defined as

It is obvious that the smaller Jkis, the higher classification accuracy will be obtained.

In order to reserve the most effective category information, the d characteristic components corresponding to the minimum Jkhave to be found out. Define the accumulated contribution rate of category information as

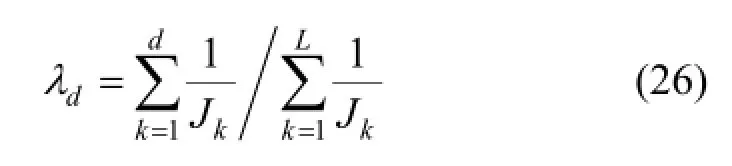
where L is the number of selected initial eigenvectors, satisfying λL> 10λL+1. Then the first d character components satisfyingλd≥are selected whereis the set value.

3 A MULTI-MODEL METHOD BASED ON FEATURE EXTRACTION USING WEIGHTED KERNEL FISHER CRITERION

The weighted between-class scatter matrix and weighted within-class scatter matrix can decrease the impacts of edge classes and outliers. The category information measurement is applied to determine the number of eigenvectors and further determine the optimal feature projection matrix. The subclasses with obvious characters can be obtained by mapping the original data into the feature space. Then, the sub-models corresponding to the subclasses are established based on support vector machine (SVM), and a switcher is used to combine all SVM sub-models.

3.1 Calculation Procedure

A multiple model is established by combining WKFDA feature extraction and the SVM algorithm. The specific calculation procedure is summarized as follows.

Step 1: Set up the initial parameters, such as the clustering number C and accumulated contribution rate for category information. The training data are initially classified by the fuzzy C-means clustering algorithm and the clustering number can be determined by the subtractive clustering [24].2

Step 2: The inner product kernel parameters σ in the l group are selected within a certain range. The eigenvectors and corresponding eigenvalues are calculated based on Eqs. (18)-(20). The eigenvectors corresponding to the first maximum Mi(i = 1,2,… ,l ) eigenvalues are selected as the initial projection matrix. Step 3: After the eigen transformation, the category information measurement Jk(k = 1,… ,Mi) is calculated by Eq. (25) and effective eigenvectors di(i = 1,2,… , l) corresponding to l group kernel parameters are determined by Eq. (26) and set value. Then the Fisher criterion values corresponding to l group effective eigenvectors are calculated and the maximum Fisher value corresponding to2σ is selected as the optimal kernel parameter. The corresponding optimal projection matrix is constituted by dieigenvectors.

Step 4: The projection transformation for training data is made by the optimal projection matrix. As to each subclass, the SVM sub-model is established by the transformed data separately.

Step 5: A switcher is used to combine SVM sub-models and then a multi-model based soft sensor is obtained.

After projection transformation of the original test sample, which subclass it belongs to is determined by the WKFDA classification algorithm. And then the test sample after transformation is input into the corresponding sub-model to calculate the output prediction. Fig. 2 shows the schematic of the proposed soft sensor, where S represents the switcher and Y is the predicted output.

3.2 Example analysis

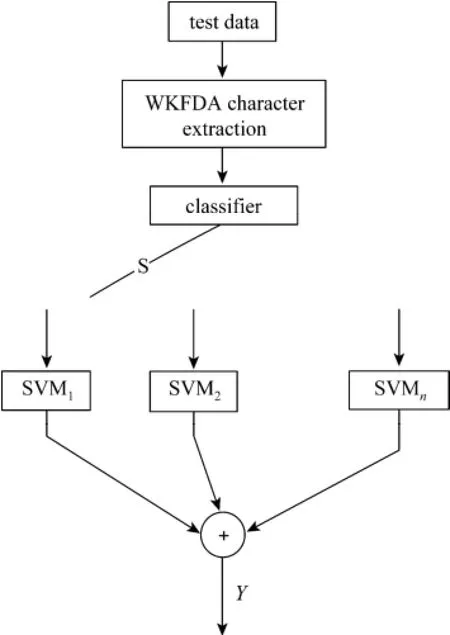
Figure 2 Schematic of the proposed soft sensor

Figure 3 Classification of the testing data

To verify the classification accuracy of the proposed method, a normal dataset of wine from UCI machine learning database [25] is used for experimental analysis. The wine dataset has 178 group sample data, including 13 input attributes and 1 category attribute. One half of the wine dataset is used as training data and the rest is used as testing data. The classification results are compared with K-nearest neighbors algorithm, Bayesian classification algorithm and decision tree algorithm. The experiment is repeated for several times and their average values are taken as the experimental results, as shown in Table 1.

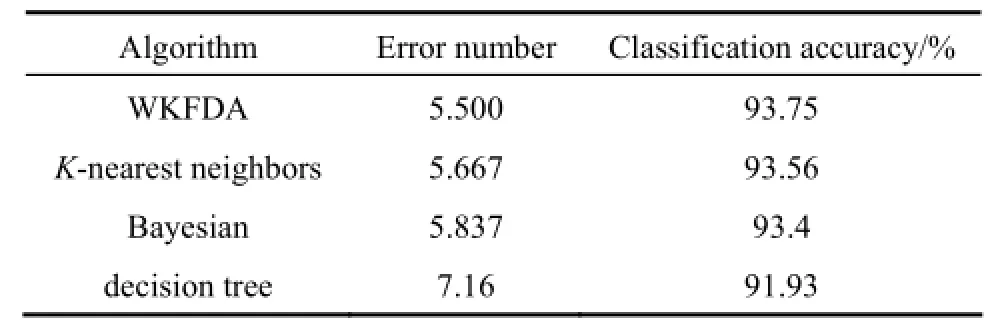
Table 1 Classification results

It is obvious that WKFDA has the highest classification accuracy. Furthermore, the sample dataset is easier to be classified after eigen transformation. The first 3 dimensions of the eigenmatrix are selected to be compared with the same dimensions of the normalized original dataset.

It is clear from Fig. 3 that the subclasses of original dataset are overlapped and the existing methods cannot separate them clearly. The proposed method can be used for eigen transformation of the original dataset so as to find out the optimal classified projection matrix. The simulation results demonstrate that the transformed data using WKFDA is easier to distinguish and classify.

4 INDUSTRIAL CASE STUDY

Crystallization process is an important step in production of bisphenol A. The online phenol content, a key quality index of a dissolution tank outlet in the crystallizer, is estimated by the proposed method. The online phenol content is subject to the following 7 main operation variables: dissolving tank temperature, tank level, vacuum filter flow rate, and the contents of 4 components from the upstream unit exiting stream. There are 284 group data collected from a production site, 4/5 of which are used for training and 1/5 for testing.

The parameters of inner kernel function are set as σ2= 2.5,= 0.8. According to the analysis for the operating condition, the number of category is C=4. KFDA and WKFDA are applied for classification and the classification results are shown in Figs. 4 and 5, respectively. From these two figures, it is obvious that the WKFDA is more effective in clustering and has better performance.

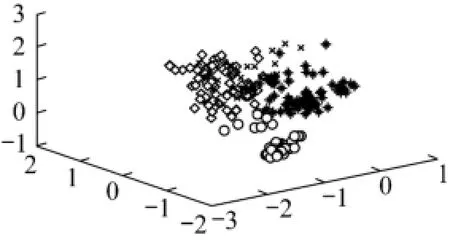
Figure 4 Classification based on KFDA extraction of training data

Figure 5 Classification based on WKFDA extraction of training data

In order to verify the effectiveness of the proposed method, a single SVM model, a multiple SVM model based on KFDA and a multiple SVM model based on WKFDA are built separately so as to do simulation comparison. The kernel parameters and punishing coefficients of single SVM model, multiple SVM model based on KFDA and multiple SVM model based on WKFDA are specified as follows:

The test errors of simulating results are shown in Table 2.

Table 2 Test errors

Table 2 demonstrates that the multiple SVM model based on WKFDA is better than the other two models. The corresponding output prediction results of testing data are shown in Fig. 6.

Figure 6 Testing curves

5 CONCLUSIONS

A new feature extraction based on a weighted kernel Fisher criterion is proposed by modifying the definition of within-class scatter matrix and betweenclass scatter matrix. The impacts of edge classes and outliers are decreased by weighting so as to avoid subclasses overlap. The weighting method is derived with a nonlinear form so that the nonlinear problems are more effectively handled. The optimal number of projection vectors is determined by category information measurement, and the better classification results are obtained. In order to further validate the effectiveness of the proposed method, an experiment is demonstrated by a normal dataset of wine from UCI machine learning database. The method is applied to a bisphenol A production process to estimate an online quality index. The simulation results validate that the classification accuracy and estimation precision are well improved by the proposed method.

REFERENCES

1 Li, X.L., Su, H.Y., Chu, J., “Multiple models soft-sensing technique based on online clustering arithmetic”, Journal of Chemical Industry and Engineering, 58 (11), 2835-2839 (2007). (in Chinese)

2 Liu, L.L., Zhou, L.F., Xie, S.G., “A novel supervised multi-model modeling method based on k-means clustering”, In: Control and Decision Conference (CCDC), Shenyang, 684-689 (2010). (in Chinese)

3 Li, N., Li, S.Y., Xi, Y.G., “Multi-model modeling method based on satisfactory clustering”, Control Theory & Applications, 20 (5), 783-788 (2003). (in Chinese)

4 Li, W.B., Sun, L., Zhang, D.K., “Text classification based on labeled—LDA model”, Chinese Journal of Computer, 31 (4), 621-626 (2008). (in Chinese)

5 Yang, Q., Ding, X., “Discrminant local feature analysis with applica tions to face recognition”, Journal of Tsinghua University (Science and Technology), 44 (4), 530-533 (2004). (in Chinese)

6 Huerta, E.B., Duval, B., Hao, J., “A hybrid LDA and genetic algorithm for gene selection and classification of microarray data”, Neurocomputing, 73 (13-15), 2375-2383 (2010).

7 Sabatier, R., Reynès, C., “Extensions of simple component analysis and simple linear discriminant analysis”, Computational Statistics and Data Analysis, 52 (10), 4779-4789 (2008).

8 Mohammadi, M., Raahemi, B., Akbari, A., Nassersharif, B., Moeinzadeh, H., “Improving linear discriminant analysis with artificial immune system-based evolutionary algorithms”, Information Sciences, 189, 219-232 (2012).

9 Chen, C.K., Yang, J.Y., Yang, J., “Fusion of PCA and KFDA for face recognition”, Control and Decision, 19 (10), 1147-1154 (2004). (in Chinese)

10 Sun, D.R., Wu, L.N., “Face recognition based on nonlinear feature extraction and SVM”, Journal of Electronics & Information Technology, 26 (2), 308-312 (2004). (in Chinese)

11 Li, Y., Jiao, L.C., “Target recognition based on kernel Fisher discriminant”, Joural of Xidian University, 30 (4), 179-183 (2003). (in Chinese)

12 Zheng, Y.J., Jian, Y.G., Yang, J.Y., Wu, X.J., “A reformative kernel Fisher discriminant algorithm and its application to face recognition”, Neurocomputing, 69 (13-15), 1806-1810 (2006).

13 Sun, J.C., Li, X.H., Yang, Y., “Scaling the kernel function based on the separating boundary in input space: A data-dependent way for improving the performance of kernel methods”, Information Sciences, 184 (1), 140-154 (2012).

14 Maldonado, S., Weber, R., Basak, J., “Simultaneous feature selection and classification using kernel-penalized support vector machines”, Information Sciences, 181 (2), 115-128 (2011).

15 Wen, Z.M., Cairing, Z., Zhao, L., “Weighted maximum margin discriminant analysis with kernels”, Neurocomputing, 67, 357-362 (2005).

16 Peng, X.J., “A v-twin support vector machine (v-TSVM) classifier and its geometric algorithms”, Information Sciences, 180 (2), 3863-3875 (2010).

17 Amari, S., Wu, S., “Improving support vector machine classifiers by modifying kernel functions”, Neural Networks, 12 (6), 783-789 (1999).

18 Kumar, M.A., Khemchandani, R., Gopal, M., Chandra, S., “Knowledge based least squares twin support vector machines”, Information Sciences, 180 (23), 4606-4618 (2010).

19 Wu, Q., “Fault diagnosis model based on Gaussian support vector classifier machine”, Eχpert Systems with Applications, 37 (9), 6251-6256 (2010).

20 He, Q., Wu, C.X., “Separating theorem of samples in Banach space for support vector machine learning”, International Journal of Machine Learning and Cybernetics, 184 (1), 49-54 (2011).

21 Loog, M., Duin, R.P.W., Haeb-Umbach, R., “Multiclass linear dimension reduction by weighted pairwise Fisher criteria”, IEEE Transactions on Pattem Analysis And Machine Intelligence, 23 (7), 762-766 (2001).

22 Li, X.H., Li, X., Guo, G.R., “Feature extraction of HRRP based on LDA algorithm”, Journal of National University of Defense Technology, 27 (5), 72-77 (2005). (in Chinese)

23 Du, S.Q., “Methods of face recognition based on kernel Fisher discriminant”, Master Thesis, Shanxi Normal University, China (2007). (in Chinese)

24 Zhang, X., “Research and application of FCM initialization method”, Master Thesis, Southwest University, China (2006). (in Chinese)

25 Frank, A., Asuncion, A., “UCI machine learning repository”, 2010, http://archive.ics.uci.edu/ml.

Received 2012-08-10, accepted 2012-10-06.

* Supported by the National Natural Science Foundation of China (61273070) and the Foundation of Priority Academic Program Development of Jiangsu Higher Education Institutions.

** To whom correspondence should be addressed. E-mail: yhz@jiangnan.edu.cn