多元Log-PH分布的CTE风险度量
2014-03-25戴泽兴王传玉
戴泽兴,王传玉,方 颢
(安徽工程大学 数理学院,安徽 芜湖 241000)
Phase-type分布,以下简称PH分布,最初是由Erlang提出。Neuts[1]定义了PH随机变量总结了一元PH分布的性质,并给出了一元PH分布的矩阵指数的表达形式。PH分布的实质是将一个时间随机变量看成是一系列与Markov过程相关联的的指数(几何)分布的时间子段之和,从而通过Markov结构来达到简化分析的目的。连续时间Markov链的一元PH分布定义为一个具有吸收状态的有限状态Markov过程的吸收时间分布。如果在此吸收状态设置一个观测点,测量此Markov链被吸收的时间,即首次到达此吸收点的时刻τ,这个随机时间的分布,就称为PH分布。因PH分布具有良好的封闭性,稠密性和可计算性,被广泛应用于生物统计学、风险理论、排队论系统、可靠性分析等领域。
连续时间Markov链的一元Log-PH,最早是由Ramaswami提出,第一次正式发表于Ghosh et al.[2]的一个会议报告中,Ramaswami[3]成功地把一元Log-PH分布应用到了排队论和可靠性分析中。Ahn[4]给出了一元Log-PH分布的具体表达式,研究了一元PH分布的k阶矩,CTE风险度量,以及尾部的渐近性。1984年,Assaf[5]给出了一类连续时间Markov链的二元PH分布。此二元PH分布的密度,Laplace变换,矩可以写成一个封闭形式。1989年,Kulkarni[6]提出了一类新的连续时间Markov链的多元PH分布。 Cai和Li[7]通过计算给出了连续时间Markov链的多元PH分布的条件尾期望风险度量(CTE风险度量)。
CTE风险度量是指在正常的市场条件下和一定的置信水平α上,测算出在给定的时间段内损失超过的条件期望值。一般来说,如果损失分布是连续的(至少对于大于相关分位数的值来说是连续的),那么,条件尾部期望可用如下公式进行计算
CTEα=E(L|L>Qα)
简而言之,CTE是当损失超过分布最差1-α部分的平均损失,这里损失分布最差1-α部分是指分布分α位点Qα之上的部分。由于其具有直观性,易于理解,通过模拟容易实现等优点,已逐渐成为精算应用领域非常重要的风险度量方法。
本文是在文献[5]和文献[7]研究的一元Log-PH分布和多元PH分布的基础上的推广,运用多元PH分布的Markov链性质,推导出关于多元Log-PH分布的最大最小分布等的CTE风险度量表达式。
1 一元PH分布的CTE风险度量
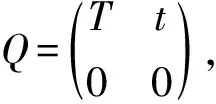
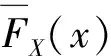
fX(x)=αexp{Tx}t,FX(x)=1-αexp{Tx}1,
其Laplace变换为
φ(s)=E[e-sx]=
(1)
k阶矩为
i=1,2,…,
矩母函数为
MX(s)=E(esx)=-α(sI+T)-1t
其中I是单位矩。
引理1[7]如果X服从参数为(α,T)的一元PH分布,对于任意的d>0,超额风险(X-d|X>d)有一个参数为(αd,T,d)的PH分布表达,其中
(2)
则对于任意的d>0
引理2[7]如果X服从参数为(α,T)的一元PH分布,对于任意的t>0,
E(X|X≤d)=
其中I是d×d维矩阵。
2 一元Log-PH分布的CTE风险度量
一元Log-PH分布,记为Log-PH(α,T),由Ramaswami最早提出。定义随机变量Y=exp(X),式中X满足参数(α,T)的一元PH分布,Y满足参数(α,T)的一元Log-PH分布。
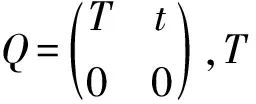
从Log-PH分布的定义,我们同样可以得到一元Log-PH分布的分布函数和密度函数的表达式
FY(y)=P(Y≤y)=P(logY≤logy)=
1-αexp{Tlogy}1,y≥1
(3)
(4)
根据Ahn S[4]文章中关于一元Log-PH分布的相关研究,一元Log-PH分布的k阶矩可以表示为
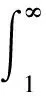
引理3[4]如果随机变量Y服从参数为(α,T)的一元Log-PH分布,那么其CTE风险度量可以表示为
CTEp[Y]=-(Qp(Y))αQp(X)(I+T)-1t
(5)
其中令d=Qp(X),Y=exp(X),p阶分位数ed=Qp(Y),那么一元Log-PH分布的CTE风险度量就可以表示为CTEp[Y]=-edαd(I+T)-1t。
3 多元Log-PH分布的CTE风险度量
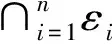

(6)
其中Q为m×m阶非退化矩阵,m=|ε|-1,令β=(0,α)为ε上的初始概率向量,那么β(△)=0。
定义
Xi=inf{t≥0;X(t)∈εi},i=1,…,n
(7)
类似于Assaf D[5],假设Pr{X1>0,…,Xn>0}=1,意味着Markov链{X(t),t≥0}以ε0开始。(X1,…,Xn)的联合分布就称为参数为(α,T,ε,ε1…,εn)的多元PH分布,转换随机变量,令Y1=expX1,…,Yn=expXn,得到的关于(Y1,…,Yn)的联合分布就为多元Log-PH分布。
Cai和Li[8]关于卷积分布S=X1+…+Xn推导出了明确的表达式。为了表述这个结论,如下定义部分空间状态
等等。
对于任意的D⊆{1,…,n},定义
k(i)=|{j:i∉εi,1≤j≤n}|
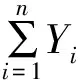
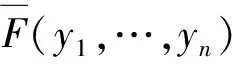
αexp{Tlogyn}gnexp{Tlogyn-1/yn}gn-1
…exp{Tlogy1/y2}g11
(8)
F(y1,…,yn)=Pr{Y1≤y1,…,Yn≤yn}=
βexp{Qlogyn}hnexp{Qlogyn-1/yn}hn-1
…exp{Qlogy1/y2}h11
(9)
其中,对于k=1,…,n,gk,定义为m×m的对角矩阵,对于i=1,…,d,若i∈εεk,该矩阵的第i个对角元素为1,否则为0。hk定义为(m+1)×(m+1)的对角矩阵,对于i=1,…,d+1,若i∈εk,该矩阵的第i个对角元素为1,否则为0。
对于(6)中的矩阵,现在引进两种Markovv链。令ε{△}=S∪S*,其中S∩S*≠φ。矩阵Q可以分段的表示如下:
(10)
此处Ts和Ts*分别是对s∉S和s∉S*的T移掉s行和s列之后得到的子矩阵,相应的,Tss*和Ts*s分别是对于s∈S*、s*∈S和s∈S、s*∈S*的T移掉s行和s*列之后得到的子矩阵。特别地,Tε{△}=T。
对于任意的Log-PH随机变量(Y1,…,Yn),类似Assaf[5]中表述的,多元Log-PH分布的极值可以表示为Y(1)=min{Y1,…,Yn}和Yn=max{Y1,…,Yn}。
定理1 令(Y1,…,Yn)服从参数为(α,T,ε,ε1,…,εn)的Log-PH分布,那么
(1)Y(1)服从参数为(α(ε0)/α(ε0)1,T(ε0)1,|ε0|)的Log-PH分布,其中T(ε0)如(10)式中定义;
(2)Y(n)服从参数为(α,T,|ε|-1)的Log-PH分布
证明:由(8)式,对于y≥0,Y(1)的生存函数为
αexp{Tlogy}gn…g11
因gn…g11=I(ε0)。对于1≤i≤n,εi都是随机封闭的,
因此Y(1)服从参数为(α(ε0)/α(ε0)1,T(ε0),
|ε0|的Log-PH分布。
同理,由(9)式,对于y≥0,Y(n)的分布函数如下
FY(n)(y)=Pr{Y(n)≤y}=F(y,…y)=
βexp{Qlogy}hn…h11=βexp{Qlogy}I({△})=
1-αexp{Tlogy}1
因此,Y(n)服从参数为(α,T,|ε|-1)的Log-PH分布。
定理2 令(Y1,…,Yn)服从参数为(α,T,ε,ε1,…,εn)的Log-PH分布,那么
(1)Y(1)的CTE风险度量为
CTEp(Y1)=-edαd(ε0)(I+T(ε0))-1t(ε0)
(2)Y(n)的CTE风险度量为
CTEp(Yn)=-edαd(I+T)-1t,
证明:令Y(k),1≤k≤n是(Y1,…,Yn中第k个最小的元素,并且服从参数为(α,T,ε,ε1,…,εn)的Log-PH分布,则(Y(1),…,Y(n))服从参数为(α,T,ε,ϑ1,…,ϑn)的Log-PH分布,其中

4 结论
本文是在一元PH分布和多元PH分布的基础上,研究的多元Log-PH分布的CTE风险度量。将这一类Log-PH分布应用到风险模型中,如假设等待时间或者索赔次数服从Log-PH分布等,以及考虑此类分布下的其他更优的风险度量,如一致性风险度量等的情况,还有待进一步研究。
参考文献:
[1] Neuts M. Matrix-Geometrie Solutions in Stoehastie Models[M].Baltimor MD:Johns Hopkins University Press ,1981.
[2] Ghosh A, Jana R, Ramaswami V, et al. Modeling and characterization of large-scale Wi-Fi traffic in public hot-spots[C].In:proc. IEEE INFOCOM 2011 Shanghai,2011.
[3] Ramaswami V. Applied probability and statistics: some challenges and opportunities(Where angels fearto tread?)[J].Computational and Mathematical Modeling, 2011:459-474.
[4] Ahn S, Kim J, Ramaswami V. A new class of models for heavy tailed distributions in finance and insure risk[J].Insurance: Mathematics and Economics,2012,51:43-52.
[5] Assaf D, Langbergn N, Savits T H, et al. Multivariate phase-type distributions[J].Operat.Res.,1984,32(3):688-702.
[6] Kulkarni V G. A new class of multivariate phase type distributions[J].Operat. Res, 1989,37(1):151-158.
[7] Cai J, Li H. Conditional tail expectations for multivariate phase-type distributions. Journal of Applied Probability[J].Journal of Applied Probability,2005,42(3):810-825.
[8] Cai J,Li H. Multivariate risk model of phase type[J].Insurance:Mathematics and Economics,2005,36:137-152.
