正交曲线坐标系基向量的二阶偏导数
2014-03-25朱文辉
陈 功,朱文辉
(1.复旦大学 力学与工程科学系, 上海 200443; 2.南通职业大学 基础课部,江苏 南通 226007)
正交曲线坐标系的引入,使物理学和工程技术中许多问题的研究得以大幅简化[1-3]。不同于直角坐标系,正交曲线坐标系的基是流动的,即为坐标的向量值函数,因此基向量对坐标的求导公式是正交曲线坐标系下计算的基础。一阶偏导数公式可参看文献[4、5]等,在场论、张量等的计算中经常会用到二阶偏导数[6,7],但统一的计算公式目前尚未见到。正交曲线坐标系基向量的偏导数是三维向量,坐标系数由拉梅系数[8]及其偏导数组成。在二阶偏导数公式的推导过程中,按照不同的求导顺序,二阶混合偏导数向量的对应系数会产生不同的表达式。本文运用基变换的单位正交性证明了当坐标函数三阶偏导数连续时拉梅系数满足的两个偏微分方程,从而上述系数的不同表达式实际上是相等的,因此基向量的二阶混合偏导数与求导顺序无关,并按4种基本类型给出了基向量的二阶偏导数公式。


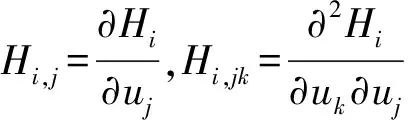
1 引理
以下3个引理给出了空间任意一点处的位置向量和单位基向量关于曲线坐标的偏导数与拉梅系数的基本关系,用于证明本文的主要结论。
引理1
(1)
(2)
证明参见文献[8]。由于i、j、k互不相同,可取1、2、3的任何一个排列,所以(1)式和(2)式实际上一共给出了9个公式。
引理2
(3)

(4)
其中i、j、k互不相同,可取1、2、3的任何一个排列。
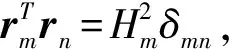


引理3 设i、j、k互不相同,为1、2、3的一个排列,记矩阵(ri,rj,rk)T=A(ijk),对角阵diag(Hi,Hj,Hk)=H(ijk),则B(ijk)=H(ijk)-1A(ijk)为正交矩阵,即B(ijk)B(ijk)T=B(ijk)TB(ijk)=E,E是单位矩阵。特别地,B(123)=H(123)-1A(123)=(e1,e2,e3)T是直角坐标到曲线坐标的基变换阵。

2 主要结论及其证明
按照不同的求导顺序计算二阶偏导数时,二阶混合偏导数向量的对应系数会产生不同的表达式,事实上,它们是相等的。下面的定理1给出了拉梅系数满足的两个偏微分方程,这两个方程正是证明这一结论的关键所在。由此,定理2证明了基向量的二阶混合偏导数与求导顺序无关,并按4种基本类型给出了基向量的二阶偏导数公式。定理1和定理2是本文的主要结论。
定理1 设i、j、k互不相同,可取1、2、3的任何一个排列,Hi为正交曲线坐标系的拉梅系数,则有
(5)
(6)
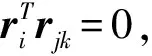

(7)
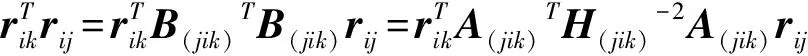
A(jik)rij=(rj,ri,rk)Trij=
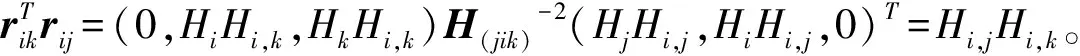
A(jik)rjk=(rj,ri,rk)Trjk=
于是
(-HiHi,j,HiHi,i,-HiHi,k)H(jik)-2(HjHj,k,0,HkHk,j)T=
下面证明公式(6)。

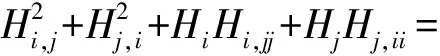
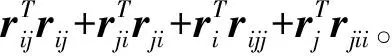
(8)
类似于(7)式的证明,有
代入(8)式,整理可得
写成向量内积的形式即为(6)式。
(5)式和(6)式表示了拉梅系数二阶偏导数满足的一种对称关系。特别地,(5)式说明第i个拉梅系数对两个异于下标的变量的二阶混合偏导数可以用一阶偏导数的算术运算直接得到。
定理2 曲线坐标系的基向量ei(i=1,2,3)的二阶偏导数有4种类型,计算公式分别为
(9)
(10)
(11)
(12)
这里i、,j、k互不相同,均表示1、2、3的一个排列。

下面推导ei,jk和ei,kj的计算公式,即(11)式,同时证明ei,jk=ei,jk。
类似地可求得
ei,kj=
比较上述两式可知,ei,jk=ei,jk当且仅当

(13)
且
(14)

最后推导公式(12),即二阶偏导数ei,ji和ei,ij,并证明ei,ji=ei,ij。
ei,ji=
(15)
(16)
(17)
比较(15)和(17)式可知,ei,ji=ei,ij当且仅当
(18)
事实上,(18)式由定理1(6)式移项可得,故ei,ji=ei,ij,且(12)式得证。
由于i、j、k互不相同,可取1、2、3的任何一个排列,所以(9)和(11)分别给出了3个公式,公式(10)和(12)分别给出了6个公式。
3 结语
包括著名的Navier-Stokes方程在内的大量流体力学运动方程由于流体复杂的几何形态,需要在与之相匹配的正交曲线坐标系中进行研究分析和计算表达,而对各种变量的求偏导数比比皆是,二阶及其以上的偏导数的计算繁琐、形式庞大。本文给出的正交曲线坐标系中基向量的二阶偏导数计算公式可以使计算大为简化,对理论研究和工程应用都有一定的实用价值。运用本文中式(9)~式(12),可以很快得出圆柱坐标系中基向量的二阶偏导数均为0;类似地,对于如球坐标系等更加复杂的正交曲线坐标系,其基向量的各个二阶偏导数亦可方便地求出。
参考文献:
[1] Erturk E, Gökçöl C. Fourth-order compact formulation of Navier-Stokes equations and driven cavity flow at high Reynolds numbers[J].Int. J. Numer. Meth. Fluids, 2006(4):421-436.
[2] Kolesnikov A, Baker A J. Efficent implementation of high order methods for the advection-diffusion equation[J].Comput. Methods Appl. Mech. Engrg, 2000(2):701-722.
[3] Tian Z F, Ge Y B. A fourth-order compact finite difference scheme for the steady streamfunction-vorticity formulation of the Navier-Stokes/Boussinesq equations[J].Int. J. Numer. Meth. Fluids, 2003(5):495-518.
[4] Matthews P C. Vector Calculus[M].London:Springer-Verlag, 1998.
[5] Gupta M M, Kalita J C. A new paradigm for solving Navier-Stokes equations:streamfunction-velocity formulation[J].J. Comput. Phys, 2005(1):52-68.
[6] Radhakrishna Pillai A C. Fourth-order exponential finite difference methods for boundary value problems of convective diffusion type[J].Int. J. Numer. Meth. Fluids, 2001(1):87-106.
[7] 周光炯,严宗毅,许世雄,等.流体力学(下册)[M].2版. 北京:高等教育出版社,2000:364-377.
[8] Zhang J. Preconditioned iterative methods and finite difference schemes for convection-diffusion[J].Appl. Math. Comput, 2000(1):1 130.
[9] 丘维声.高等代数(上册)[M].北京:清华大学出版社,2010.
