滑翔式高超声速飞行器双环结构协调解耦控制
2014-03-25靳锴罗建军苏二龙闵昌万黄兴李闫颖鑫
靳锴, 罗建军, 苏二龙, 闵昌万, 黄兴李, 闫颖鑫
滑翔式高超声速飞行器具有飞行速度快、突防能力强和远程精确投送等特点,因此有着极其重要的军民两用价值[1-4]。高超声速飞行器飞行环境复杂,再加上飞行模式的特殊性,使得飞行器控制系统成为一个具有强不确定性、强耦合性、非线性和时变性的复杂对象。滑翔式高超声速飞行器的姿态控制问题可归结为存在强耦合、强不确定性的大包线下高精度解耦控制问题。
近年来,针对高超声速飞行器控制系统设计开展了很多理论研究,主要集中在模糊控制、动态逆控制、鲁棒控制、滑模控制等方法。Austin等人利用遗传算法设计了模糊逻辑控制器[5],并对验证机X-34进行了仿真验证。这种控制方案的优点是不需要对飞行器的模型和动态特性线性化,其缺点是需要大量的专家经验。Wu等人基于模糊逻辑方法研究了X-38再入大气层时的姿态控制问题[6],将飞行器的再入过程分为5个飞行阶段,各阶段采用不同的执行机构分配策略,以实现全轨迹控制,其不足之处在于分配策略切换时会产生振荡。Mcfarlane与Glover利用互质分解的方法将H∞理论和回路成形方法相结合,提出了鲁棒H∞回路成形方法[6],所设计的控制系统具有突出的鲁棒解耦性能和优良的动静跟踪响应,该方法进行解耦控制时将滚转通道角速度值设为定值,因此在飞行器滚转通道角速度变化时,解耦效果大大降低。Jennifer等人采用了双环控制结构,研究了X-38再入大气层时的姿态控制问题[8]。作者通过动态逆的方法来设计内环回路,保证飞行器的性能,利用极点配置法设计外环回路,保证整个系统的稳定性,但这种方法要求模型精确度极高。针对BTT式飞行器存在强耦合的特点,A. Arrow采用了协调控制的方法对飞行器的耦合进行了较为有效抑制[9-10],但没有给出解耦回路中参数选取的具体方法。
本文针对滑翔式高超声速飞行器的耦合作用强、飞行包线大的特点,采用基于快、慢变量的双环结构与协调解耦控制相结合的方法设计飞行器控制系统,并给出解耦增益选取的一般方法。整个控制系统采用双环反馈结构,并依据协调解耦原理在控制系统中引入解耦回路实现通道间的解耦。双环反馈结构将状态变量依据时间尺度进行分阶控制,内环实现角速度控制,保证飞行器的动态性能,外环实现角度控制,保证整个系统的稳定性。最后通过定点仿真、参数拉偏仿真及大包线全轨迹飞行仿真,对控制系统的性能进行了检验,验证了控制系统设计的有效性。
1 飞行器动力学模型
滑翔式高超声速飞行器采用面对称气动布局和无动力飞行。假设飞行器为刚体;忽略重力的影响,只考虑飞行器在飞行过程中受到的空气动力;质量与质心位置不变[11]。根据上述假设,可建立体坐标系下的姿态动力学模型为:
(1)
式中:α、β、γ为飞行器的攻角、侧滑角、倾侧角;ωx、ωy、ωz为飞行器的滚转角速度、偏航角速度、俯仰角速度;δx、δy、δz分别为飞行器副翼偏角、方向舵偏角、水平舵偏角;Jx、Jy、Jz为飞行器相对体坐标系三轴的转动惯量;S、L分别为飞行器特征面积和特征长度;q为来流动压,m为飞行器质量,V为飞行器瞬时速度。
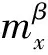
2 控制系统设计
双环结构协调解耦控制系统结构图如图1所示。控制系统分为控制回路与解耦回路2部分。其中控制回路由内外2个反馈回路组成,内环实现快变量角速度控制,保证飞行器的动态性能;外环实现慢变量角度控制,保证整个系统的稳定性[12],如图1中所示的实线部分。解耦回路由角速度解耦回路f1与舵偏解耦回路f22部分组成,如图1中所示虚线部分。
2.1 解耦回路设计
由(1)式所示姿态动力学模型可以看出,6个状态量中除倾侧角γ外的5个状态量都存在耦合作用,在控制系统设计时需要进行解耦,才能实现精确控制。这5个状态量之间虽存在着复杂的耦合作用,却又都受到角速度控制信号与舵偏控制信号的控制,采用如图1所示的快、慢变量双回路反馈系统,能够实现对动力学模型的精确解耦。
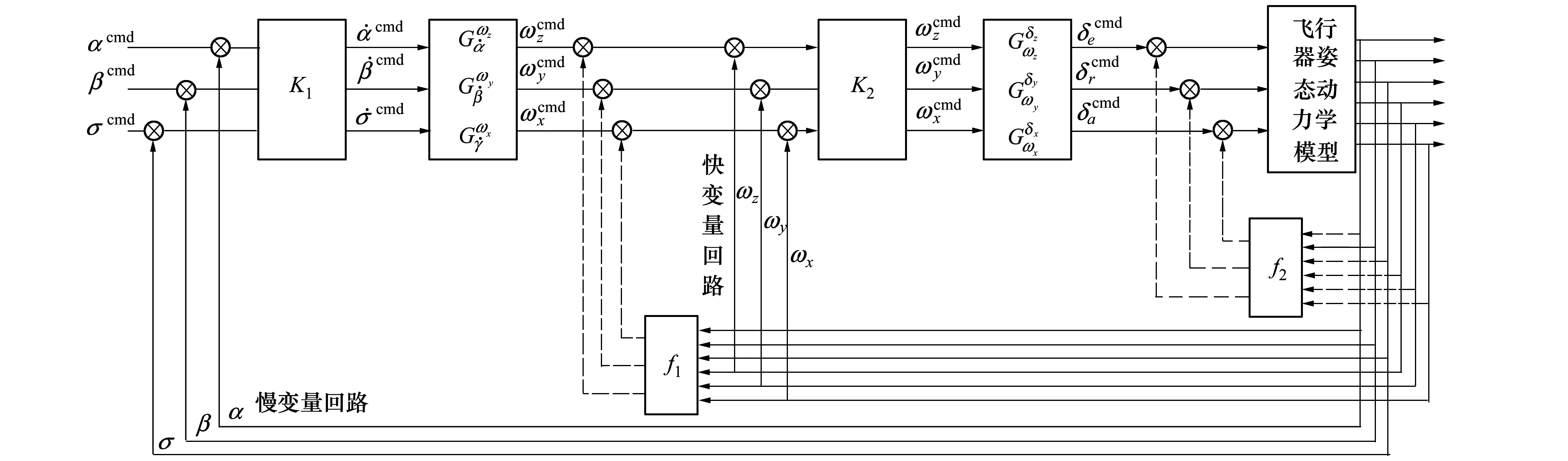
图1 控制系统结构图
定义ωc=ω+Δωc,δc=δ+Δδ。其中,ωc为角速度控制信号,ω为角速度反馈信号,Δωc为解耦角速度信号,用来抵消姿态角方程中的耦合作用;δc为舵机执行舵偏;δ为理想控制舵偏,即在不考虑耦合时,为使飞行器达到理想状态所需舵偏;Δδ为解耦舵偏,即用来抵消各角速度方程中的耦合作用所需舵偏。执行机构按照δc进行机动,既可以抵消设计之外来自其他通道的耦合作用,又可使飞行器按期望的指令飞行。将ωc、δc代入(1)式进行整理,并将耦合项、解耦舵偏、解耦角速度与其他项分离可得解耦状态方程:
(2)
方程(2)给出了解耦舵偏、解耦角速度与状态参数之间的关系。通过选取合适的解耦角速度、解耦舵偏控制信号,可使得由耦合项造成的状态参数误差值为零或近似为零,实现对动力学模型的解耦。
对(1)式所示的姿态动力学模型进行解耦,得到解耦后的姿态动力学模型为:
(3)
以某型飞行器气动参数为设计数据,选取速度为3 172 m/s,高度为40 000 m的特征点进行控制系统解耦。选取5条解耦回路分别为:Δδx=kc1β+kc2δy,Δδy=kc3ωxωz+kc4δx,Δδz=kc5ωxωy,Δωy=kc6ωxα,Δωz=kc7ωxβ。计算可得解耦增益分别为:kc1=-1.240 0,kc2=-0.064 5,kc3=0.833 4,kc4=-0.995 7,kc5=-0.087 4,kc6=-1.012,kc7=1.059。
2.2 控制回路设计
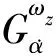
选取速度为3 172 m/s,高度为40 000 m的特征点进行控制回路设计,得到的俯仰、偏航、滚转3个通道的控制器如下:

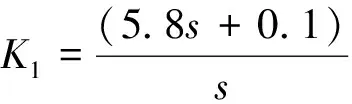
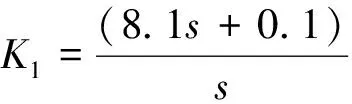
2.3 全轨迹控制策略
在对特征点上的解耦回路和控制回路进行有效设计的基础上,要实现大包线全轨迹控制,必须采用适合的控制策略,在不同的飞行条件下进行增益调度。针对双环结构协调解耦控制系统采用的全轨迹控制策略的基本思想是保持整个控制系统结构不变,根据动压与攻角选取多个特征点并进行参数设计,在不同的飞行状态下选取不同的控制器参数与解耦增益进行解耦与控制。全轨迹控制框图如图2所示。
这种全轨迹控制的显著优点主要有如下2点:①只进行增益调度不进行控制器结构切换可以避免不必要的振荡;②控制参数与解耦增益同时进行调度,从而保证实时精确解耦与控制。采用这种全轨迹控制策略能使飞行器在全轨迹上任意一点都拥有最好的解耦效果和控制效果。
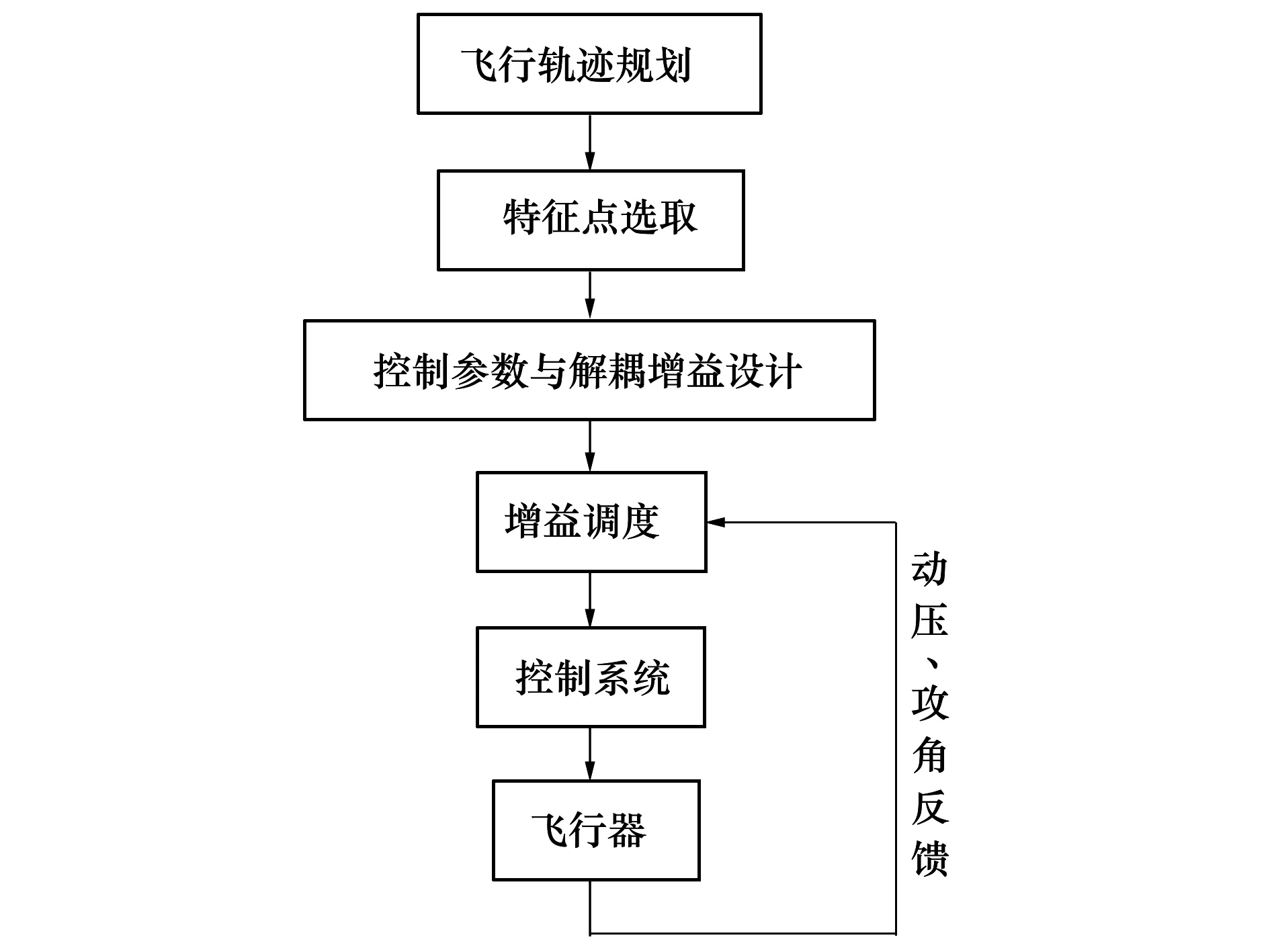
图2 全轨迹控制框图
3 仿真分析
仿真中的非线性模型采用旋转球状地面动力学模型[13]与姿态动力学模型,其中姿态动力学方程包含一阶近似和二阶小项。
仿真工作主要包括:参数拉偏仿真,验证控制系统的抗扰动鲁棒性能;全轨迹仿真,验证控制方法全轨迹飞行性能和全轨迹控制策略的正确性。仿真中考虑工程可实现性对舵偏范围进行如下限制:-20°≤δx≤20°;-20°≤δy≤20°;-30°≤δz≤10°。
3.1 参数拉偏仿真
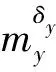
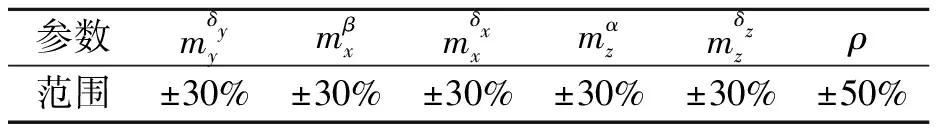
表1 不确定性参数取值
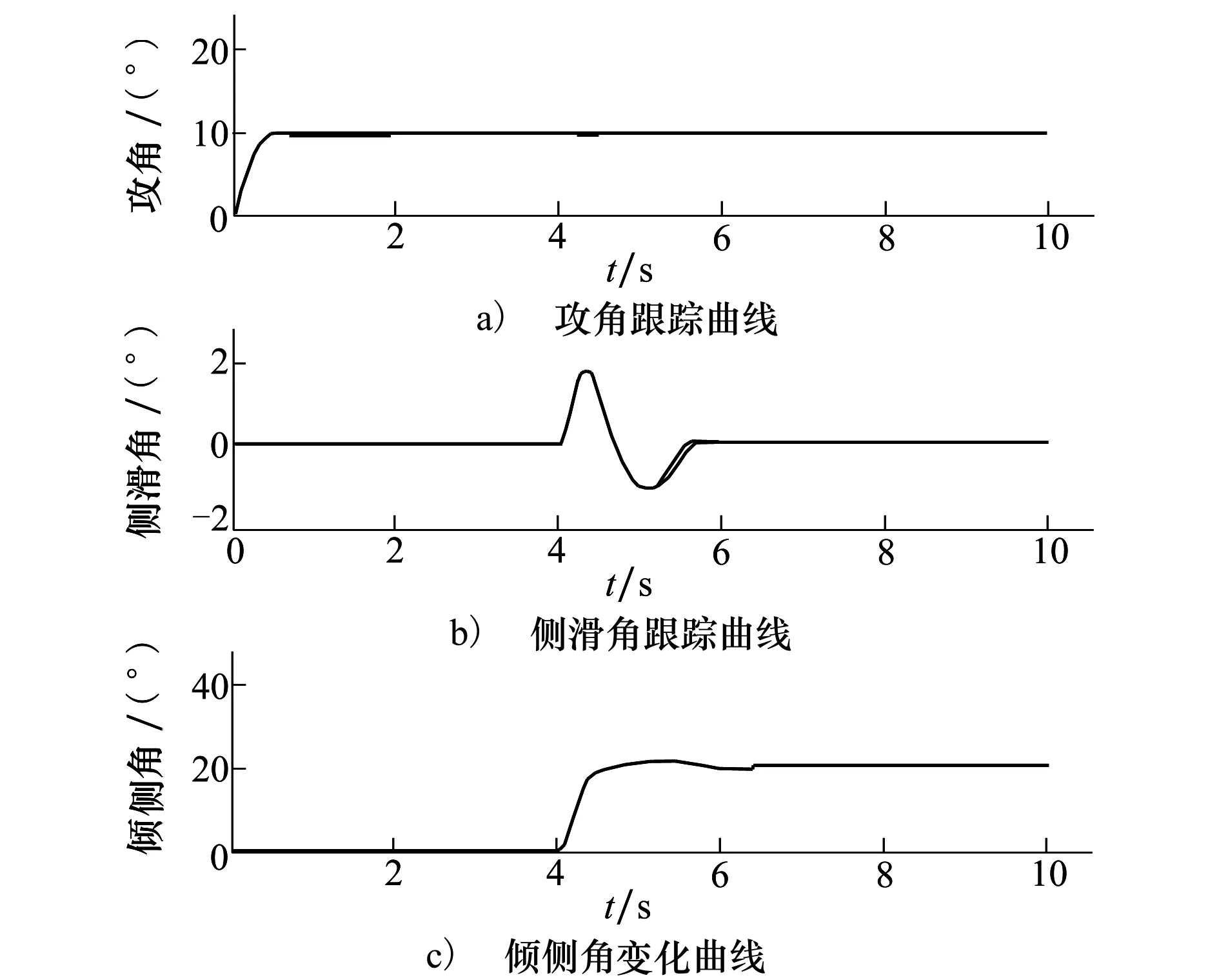
图3 参数拉偏条件下的姿态响应曲线
由图3可知,在对高灵敏度参数进行大范围拉偏的情况下,控制系统仍然能稳定跟踪控制指令,且姿态角响应曲线,具有较好的抗扰动鲁棒性。
3.2 全轨迹仿真
为验证控制系统的全轨迹飞行可行性与全轨迹控制策略的正确性,进行全轨迹设计与仿真。
根据标称轨迹中的攻角曲线与标称动压曲线,选取多个特征点,对每个特征点进行控制参数与解耦增益的设计,采用图2的全轨迹控制策略进行全轨迹仿真。图4~图7给出了指令角度与轨迹跟踪曲线。
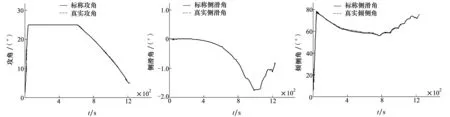
图4 攻角指令跟踪曲线 图5 侧滑角变化曲线 图6 倾侧角指令跟踪曲线

图7 三维轨迹跟踪曲线
从全轨迹仿真结果可以看出,控制系统在大包线范围内能够很好地跟踪设计轨迹,采用插值法的全轨迹增益调度策略没有产生振荡。从3个角度指令跟踪曲线来看,攻角基本无误差的跟踪控制指令信号,且响应十分迅速;倾侧角在初始时刻由于进行快速机动,产生了小幅振荡但很快消失,能高精度地跟踪指令;侧滑角始终保持在±2°之内,能够满足设计要求。以上仿真结果表明所设计的双环结构协调解耦控制系统能够实现滑翔式高超声速飞行器在大包线内对轨迹的精确跟踪。
4 结 论
本文针对滑翔式高超声速飞行器飞行包线大,三通道之间的耦合作用强的特点,提出并采用了基于快、慢变量的双环控制结构与协调解耦控制相结合的设计方法对飞行器控制系统进行设计,并通过基于simulink的非线性参数拉偏仿真和全轨迹仿真对控制系统的解耦能力、抗扰动鲁棒性、轨迹跟踪控制能力进行了验证。仿真结果表明:采用该方法设计的控制系统能够进行有效地解耦与控制,具有很强的抗扰动鲁棒性,能够实现飞行器大包线下全轨迹精确跟踪。
参考文献:
[1] Morelli E A, Derry S D, Smith M S. Aerodynamic Parameter Estimation for the X-43A(Hyper-X) from Flight Data[C]∥2005 AIAA Guidance, Navigation, and Control Conference and Exhibit, San Francisco
[2] Karlgaard C D, Martin J G, Tartabini P V, et al. Hyper-X Mach 10 Trajectory Reconstruction[C]∥2005 AIAA Atmospheric Flight Mechanics Conference and Exhibit, San Francisco
[3] Rodriguez A A, Dickeson J J, Cifdaloz O, et al. Modeling and Control of Scramjet-Powered Hypersonic Vehicle: Challenges[R]. AIAA-2008-0679
[4] 刘鹏, 谷良贤. 高超声速飞行器动态输出反馈最优跟踪控制[J]. 哈尔滨工业大学学报, 2011, 43(7): 131-134
Liu Peng, Gu Liangxian. Dynamic Output Feedback Based Optimal Tracking for Hypersonic Flight Vehicles[J]. Journal of Harbin Institute of Technology, 2011, 43(7): 131-134 (in Chinese)
[5] Austin K J, Jacobs P A. Application of Genetic Algorithms to Hypersonic Flight Control[C]∥IFSA World Congress and 20th NAFIPS International Conference, 2001
[6] Wu S F, Engelen C J H, Babuska R, et al. Intelligent Flight Controller Design with Fuzzy Logic for an Atmospheric Re-Entry Vehicle[C]∥Proceedings of the 38th Aerospace Sciences Meeting and Exhibit, Reno, NV, 2000
[7] Mcfarlane D, Glover K. A Loop Shaping Design Procedure UsingH∞Synthesis [J]. IEEE Trans on Automatic Control, 1992, 37(6): 759-769
[8] Jennifer Georgie, John Valasek. Selection of Longitudinal Desired Dynamics for Dynamic Inversion Controlled Re-Entry Vehicles [C]∥AIAA Guidance, Navigation, and Control Conference and Exhibit, Canada,2001
[9] Arrow A. An Analysis of Aerodynamic Requirements for Coordinated Bank-to-Turn Auto Pilots [C]∥NASA-CR-3644,1982
[10] Arrow A. Status and Concerns for Bank-to-Turn Control of Tactical Missiles [J]. Journal of Guidance, Control, and Dynamics, 1985, 8: 267-274
[11] Keshmiri S, Mirmirani M D, Colgren R D. Six-DOF Modeling and Simulation of a Generic Hypersonic Vehicle for Conceptual Design Studies[C]∥AIAA Modeling and Simulation Technologies Conference and Exhibit, 2004
[12] 安相宇,王小虎. 高超声速滑翔飞行器动态逆解耦跟踪控制方法研究[J]. 系统仿真学报, 2010, 22: 107-110
An Xiangyu, Wang Xiaohu. Research of Dynamic Inversion Decoupling Tracking Control Method for Hypersonic Sliding Vehicle[J]. Journal of System Simulation, 2010, 22: 107-110 (in Chinese)
[13] Vinh N X, Baseman A, Culp R D. Hypersonic and Planetary Entry Flight Mechanics[M]. The Univerity of Michigan Press, Ann Arbor, 1990
