HGT准双曲面齿轮传动的轮齿接触分析

王星, 方宗德, 李声晋, 高正国, 宁程丰

(1.西北工业大学 机电学院, 陕西 西安 710072; 2.青岛中集冷藏运输设备有限公司, 山东 青岛 266300)

准双曲面齿轮是齿轮传动中最为复杂的一种，其几何形状与啮合理论非常复杂，一直是齿轮制造过程中的难点。同时它又是汽车驱动桥中的关键零部件，而准双曲面齿轮的啮合质量是通过正确的切齿设计来保证的，国内不少学者对这方面的工作做了深入的研究。

格里森准双曲面齿轮常用的切齿方法有4种，代号分别为HFT、HFM、HGT和HGM。由于HFT大轮采用成形法加工，工件和摇台均不转动，由刀盘直接回转加工出齿面，从而具有加工效率高的特点，因此，在汽车工业中得到了广泛应用，它也是目前使用最多的准双曲面齿轮的切齿方法。唐进元等[1]针对HFT准双曲面齿轮，推导了齿面方程和过渡曲面方程。方宗德等[2]针对HFT准双曲面齿轮，推导了齿轮传动的轮齿接触分析方法。李慧[3]针对HFM法利用空间啮合几何学和空间坐标变换，建立了大、小轮切齿加工的数学模型和齿面表达的非线性方程组。Simon[4]研究了如何在数控机床上加工准双曲面齿轮。吴序堂[5]对HGT准双曲面齿轮切齿方法做了深入的理论研究。对于HGT准双曲面齿轮，大轮采用展成法加工，加工效率没有成形法高，但是展成法(generated)与成形法(formated)相比，其优越之处就是可以设置齿轮具体的啮合性能，且自从弧齿锥齿轮与准双曲面齿轮加工机床出现以来，刀倾法(tilt)的出现和引入齿轮加工中是齿轮加工制造技术的一大突破，因此，有必要对HGT准双曲面齿轮进行理论齿面推导及相应的啮合仿真，为进一步的研究打下基础。

轮齿接触分析(TCA)，包括齿面接触分析[6]和边缘接触分析[7]，代表了齿轮啮合的完整过程。边缘接触是一种轮齿齿顶边缘传递运动的现象，当边缘接触发生时，由于两接触曲面的位置关系不确定，因此不能应用微分几何求解在接触曲面上的主曲率方向。对于准双曲面齿轮，边缘接触是极易发生的,如何正确确定在接触曲面上的主方向，将对齿轮副的承载接触分析产生较大影响。方宗德教授对该问题进行了研究，提出了通过“数值方法”在接触点邻近曲面范围内产生主方向并得到沿该方向离散点处齿面间隙的方法[8-9]。为了问题的简化，近似取两齿面啮合点接触椭圆的长轴方向作为边缘接触曲面的主方向。

本文采用空间啮合理论，推导了HGT准双曲面齿轮齿面的表达方法，便于进行计算机仿真和生成轮齿模型，以便我们准确得出不同参数、不同误差的齿轮啮合过程和性能，能有效降低产品成本、提高产品质量，并对该对齿轮进行了轮齿接触分析，并以算例验证了边缘接触分析的重要性。

1 理论齿面的表达

1.1 大轮理论齿面

大轮采用展成法加工，小轮采用刀倾法加工，这时的产形轮是锥形产形轮，产形轮和齿轮之间有相对运动，刀盘的切削面和齿面是一对完全共轭的曲面。大轮和小轮的切齿刀具如图1a)、图1b)所示。

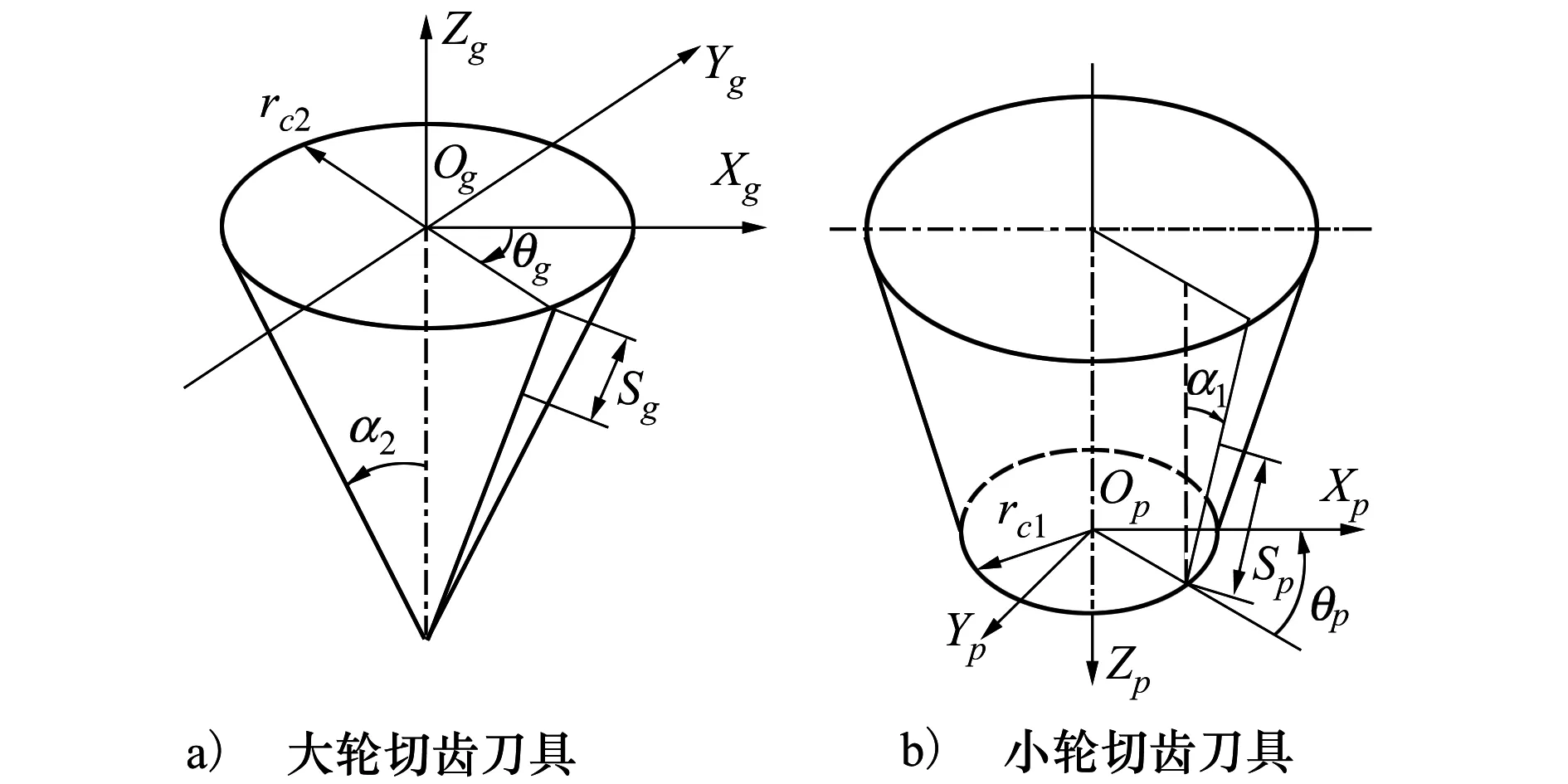
图1 大轮和小轮切齿刀具

图中,rc2和rc1是刀尖半径,αg和αp为刀具齿形角,大轮的刀具齿面用参数θg、和Sg表示为:

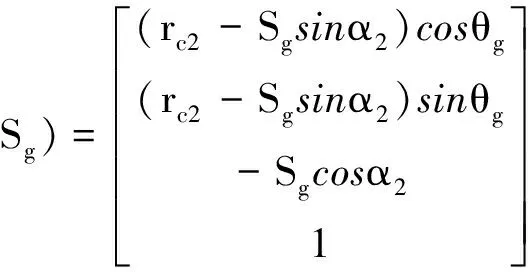
(1)

(2)

图2 大轮和小轮切齿坐标系

大轮和小轮的切齿坐标系如图2a)、图2b)所示，其中，图2a)是大轮切齿坐标系，Og是刀具中心，Oc2是摇台中心，O2是齿轮的设计交叉点(齿轮轴线与2条轴线间距离线的交点)，坐标系Sp、Sc2、Sa固定在机床上，Sg和S2分别固定在刀具和被加工齿轮上，φg和φ2分别为摇台转角和大轮的加工转角。

根据图2a)中坐标关系,齿面在S2中的表达式为:

(3)

(4)

式中:M为4×4坐标转换矩阵,L为其中的3×3转动部分。切削时刀具形成的假想齿面与大轮齿面啮合,因此须满足以下啮合方程[7]:

f2=N2·R2

(5)

联合求解(1)式～(5)式,经过不断迭代,可得到大轮理论齿面方程。

1.2 小轮理论齿面

根据图1b)所示,小轮的刀具齿面用参数θp、φp和Sp表示为:

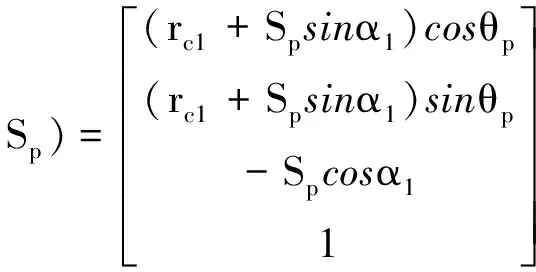
(6)

(7)

图2b)是小轮切齿坐标系,经过与大轮齿面的表达相似的推导,得到小轮齿面在坐标系S1(固定在小轮上)中的表达式为:

(8)

(9)

同理,切削时刀具形成的假想齿面与小轮齿面啮合,因此也必须满足以下啮合方程[7]:

f1=N1·R1

(10)

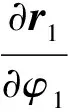
联合求解(6)式～(10)式,经过不断迭代,可得到小轮理论齿面方程。

2 轮齿接触分析

2.1 齿面接触分析

计及安装误差的齿轮啮合坐标系如图3所示。

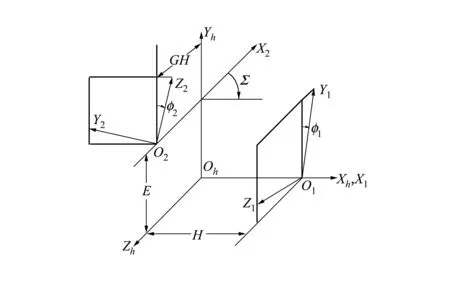
图3 齿轮副啮合坐标系

图中O1和O2为设计交叉点,坐标系Sh固定在箱体上,S1和S2分别固定在小、大齿轮上,ψ1和ψ2分别是啮合时小轮和大轮转角,Σ为轴交角,E为偏置距。根据图中坐标关系,大轮齿面在Sh中的表达式为:

(11)

(12)

式中:Sa、Sb、Sc和Sd为辅助坐标系。

小轮齿面在Sh中的表达式为:

(13)

(14)

2个齿面的啮合条件为:

(15)

(15)式表示的矢量方程中包含了6个标量方程,由于n是单位矢量,独立的方程数为5个,再加上2个啮合方程,因此共有7个独立的标量方程,而未知数为θg、φg、Sg、ψ2、θp、φp、Sp、ψ1共8个。此时可按一定步长选择ψ1,求解非线性方程组(15),解出其余的7个未知数,将以上求得的8个参数代入(3)式、(4)式和(8)式、(9)式中,分别得到坐标系S2和S1中的接触点。在整个啮合过程中,以一定的步长选定ψ1,重复以上计算,直至求出的接触点超出齿面的有效边界,即可得到大轮和小轮齿面的接触点轨迹。

对于每一个瞬时接触点,齿轮刀具表面的主曲率和主方向都是已知的,根据图2所示的切削坐标和相对运动关系,可以计算得到齿面上该点的主曲率和主方向,并根据事先给定的弹性变形量d≤0.006 35 mm[10],进而得到瞬时接触椭圆的长轴方向与尺寸,即齿面啮合印痕。

此外,还可由ψ1和ψ2获得齿轮副的传动误差曲线。传动误差函数[2]由下式定义:

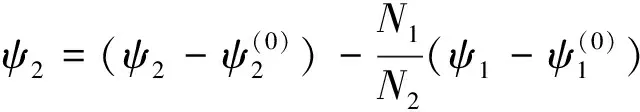
(16)

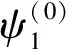
根据以上计算得到的一组ψ1和ψ2,可以给出整个啮合过程中的传动误差曲线。啮合印痕与传动误差是齿面接触分析的主要结果,比较完整地表达了齿轮副在空载或轻载下的啮合性能。

2.2 边缘接触分析

当退出啮合时,小轮的齿顶边缘与大轮的齿面可能相接触。这时,在啮合坐标系Sh中小轮的齿顶边缘与大轮的齿面有相同的位置矢量,且小轮的齿顶边缘切矢量一定与大轮的齿面法矢垂直[5]。因此,有:

r1h(θp,φp,Sp,ψ1)=r2h(θg,φg,Sg,ψ2)

(17)

(18)

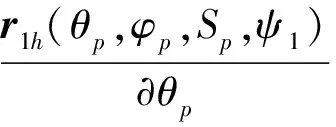
f1=N1·R1

(19)

以及大轮刀具和大轮的啮合方程[7]:

f2=N2·R2

(20)

再加上一个辅助方程:

(21)

共有7个独立的标量方程。

经过齿面接触分析与边缘接触分析后,就可以比较完整地得到TCA求解过程。

3 算 例

将准双曲面齿轮的切齿设计与轮齿接触分析编制成计算机程序,以一对格里森准双曲面齿轮为例,对轮齿进行了啮合过程仿真,其主要参数及切齿参数如表1、表2所示。

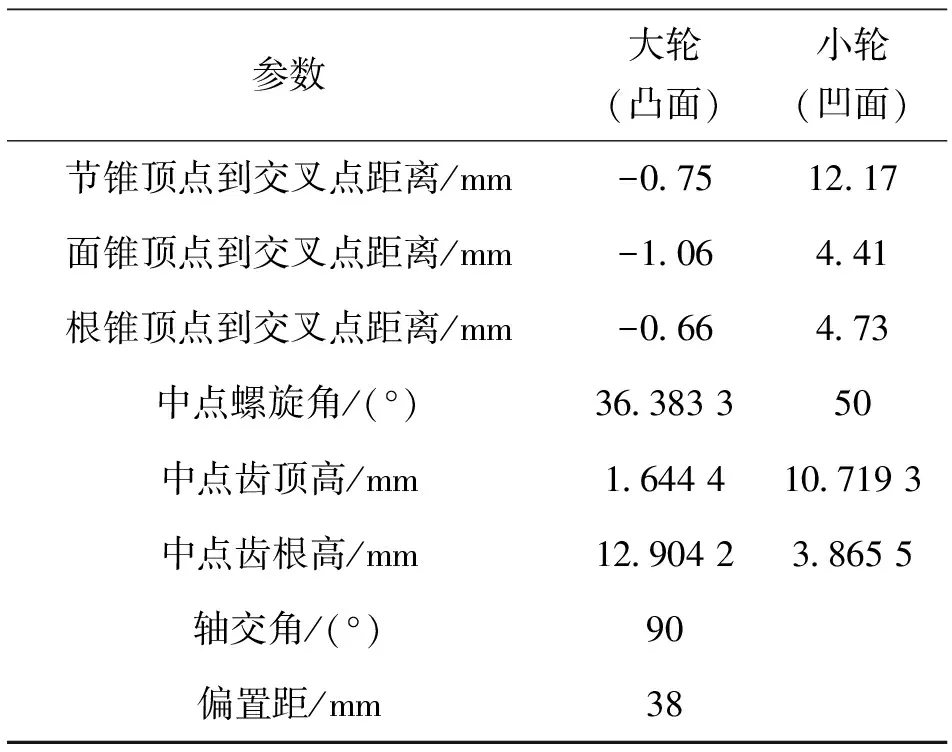
表1(续)

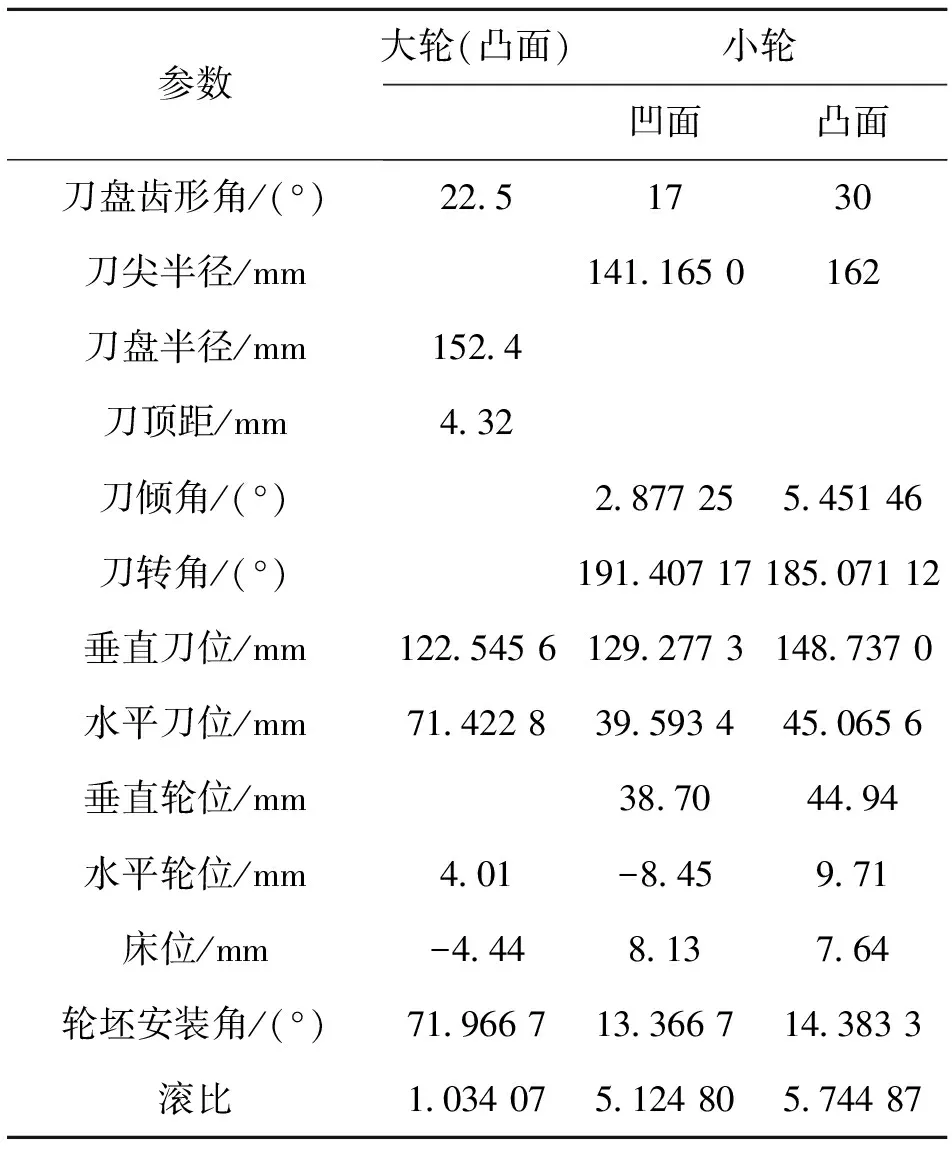
表2 切齿参数

轮齿接触分析结果如图4、图5和图6所示。

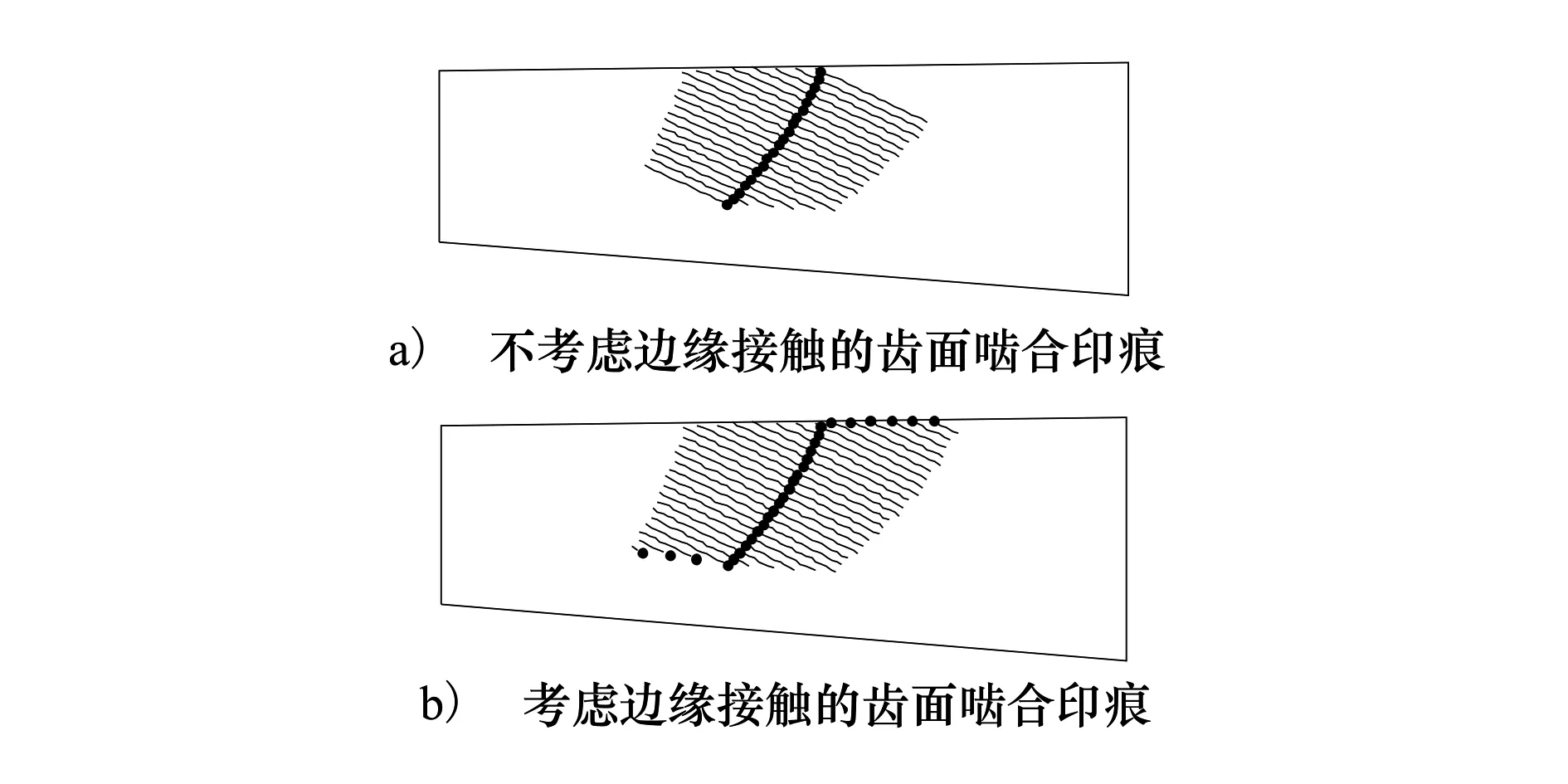
图4 不考虑安装误差时的齿面啮合印痕

图5 不考虑安装误差时的传动误差曲线 图6 考虑安装误差时的TCA分析结果

图4和图5分别为在没有考虑安装误差的情况下齿面啮合印痕和传动误差曲线。由图4可以看出,齿轮在进入和退出啮合时都发生了边缘接触,由图5可以看出,在考虑边缘接触时,传动误差呈现了一定的对称性,且形成了较大的幅值,该图所示结果形象地说明了齿轮传动由边缘接触向下一对齿过渡的连续过程。

根据国标GB 11365-89表18,当轴夹角有0.000 3 rad安装误差时的轮齿接触分析结果如图6所示,其中,图6a)没有考虑边缘接触,图6b)考虑了边缘接触。可以看出,啮合区向大轮小端移动,图6b)中传动误差呈现了一定的对称性,且幅值有明显的下降。

边缘接触分析的结果对于进一步的强度分析和振动分析都有很重要的意义。

4 结 论

本文以一对格里森准双曲面齿轮副为研究对象,讨论了加工方法HGT坐标系的建立及齿面方程的推导,并对齿轮副进行了轮齿接触分析,得到如下结论:

1) 建立了格里森HGT准双曲面齿轮的切齿加工数学模型,推导了理论齿面方程。

2) 对齿轮进行了轮齿接触分析,包括齿面接触分析和边缘接触分析,并编制成计算机程序,可以比较完整地对齿轮在空载或轻载下的啮合过程进行准确的仿真,验证了数学模型和理论推导的正确性。

3) 在此研究的基础上可以进行齿面承载接触分析等方面的研究。

CNC锥齿轮机床的出现开创了锥齿轮加工装备的新纪元,如何通过运动转换在CNC机床上实现HGT准双曲面齿轮的加工有待进一步研究。

参考文献：

[1] 唐进元,聂金安. 含过渡曲面的准双曲面齿轮精确三维几何建模方法[J]. 机械科学与技术,2010,29(3):358-363

Tang Jinyuan, Nie Jin′an. A Method for Accurate Modeling of a Hypoid Gear with Fillet [J]. Mechanical Science and Technology for Aerospace Engineering, 2010, 29(3): 358-363 (in Chinese)

[2] 方宗德,杨宏斌. 准双曲面齿轮传动的轮齿接触分析[J]. 汽车工程,1998, 20(6):350-355

Fang Zongde, Yang Hongbin. Tooth Contact Analysis of Hypoid Gears [J]. Automotive Engineering, 1998, 20(6): 350-355 (in Chinese)

[3] 李慧. 基于数控铣齿机的准双曲面齿轮HFM法加工[D]. 郑州:河南科技大学,2005

Li Hui. HFM Method of Hypoid Gear on NC Gear Milling Machine[D]. Zhengzhou: Henan University of Science and Technology, 2005 (in Chinese)

[4] Simon V V. Generation of Hypoid Gear on CNC Hypoid Generator[J]. Journal of Mechanical Design, 2011,133(12): 1-9

[5] 吴序堂. 格里森制准双曲面齿轮刀倾全展成切齿法的研究[J]. 机械工程学报,1985,21(2):54-69

Wu Xutang. Study on the Cutter Tilt Generating Cutting Methods of Gleason Hypoid Gear [J]. Chinese Journal of Mechanical Engineering, 1985, 21(2): 54-69 (in Chinese)

[6] 曾韬. 螺旋锥齿轮设计与加工[M]. 哈尔滨:哈尔滨工业大学出版社,1989: 237

Zeng Tao. Design and Manufacture of Spiral Bevel Gears [M]. Harbin: Harbin Institute of Technology Press, 1989: 237 (in Chinese)

[7] Litvin F L. Gear Geometry and Applied Theory [M]. Englewood Cliffs, NJ: PrenticeHall, 1994: 106, 282

[8] 方宗德,邓效忠,任东锋. 考虑边缘接触的弧齿锥齿轮承载接触分析[J]. 机械工程学报,2002, 38(9): 69-73

Fang Zongde, Deng Xiaozhong, Ren Dongfeng. Tooth Contact Analysis of Spiral Bevel Gear Considering the Edge Contact [J]. Chinese Journal of Mechanical Engineering, 2002, 38(9): 69-73 (in Chinese)

[9] 高建平,方宗德. 螺旋锥齿轮边缘接触分析[J]. 航空动力学报,1998,13(3):289-292

Gao Jianping, Fang Zongde. Edge Contact Analysis of Spiral Bevel Gear [J]. Journal of Aerospace Power, 1998, 13(3): 289-292 (in Chinese)

[10] 方宗德,郭琳琳,苏进展,等. 基于齿面印痕控制的弧齿锥齿轮公差优化设计[J]. 农业机械学报,2011,42(7):223-228

Fang Zongde, Guo Linlin, Su Jinzhan, et al. Optimal Design of Tolerance for Spiral Bevel Gears by Controlling Contact Path [J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(7):223-228 (in Chinese)