基于文化粒子群算法的开关磁阻电机多目标优化设计

宋受俊, 葛乐飞, 蒋艳玲

(西北工业大学 自动化学院, 陕西 西安 710072)

开关磁阻电机(SRM)是一种极具竞争力的新型机电一体化设备，它具有启动转矩大、调速范围宽、控制灵活、可靠性较高、适应恶劣环境以及成本较低等诸多性能优势[1]，在多电飞机[2]、电动汽车[3]、风力发电[4]、主轴驱动，家用电器等领域具有广阔的应用前景和巨大的发展潜力，近年来受到广泛关注。然而运行效率偏低以及转矩脉动较大等缺陷成为了限制SRM应用及推广的技术瓶颈，如何快速而准确地对其进行优化设计与控制一直是研究的热点问题。

铁心磁密的高度饱和以及开关型供电模式使SRM驱动系统成为了一个多变量、强耦合的非线性系统，其设计及控制方法的研究面临着极大的困难。国内外学者在该方面做了大量的工作，取得了一定的进展[5]，但研究还不够深入。目前，绝大多数设计仍然建立在类比法、经验公式或有限元法基础之上[6-8]，过程繁琐，专业性要求高，且难以获得最优方案，只有极少数学者在其设计中引入了优化算法[9-12]。

文化粒子群优化算法(CPSOA)利用文化算法(CA)特有的双重进化构架来引导粒子群算法(PSO)的搜索过程，提高其全局搜索能力，避免陷入局部最优[13-14]。从提出至今，CPSOA及其改进算法已在水库防洪调度、电力系统经济负荷分配、变电站选址与定容、神经网络参数优化、机械工程设计等方面得到了应用[15-16]，并获得了良好的效果。

通过仔细的调查分析发现，至今还没有将CPSOA应用于电机系统设计的研究。本文在SRM的优化设计及控制中首次引入了CPSOA，在一定的优化目标及约束下，快速而准确地得到了关键几何尺寸和控制参数的全局最优解，从而验证了方法的有效性，显示了其性能优势。

1 文化粒子群算法

粒子群算法是一种基于群体进化理论的优化算法，源于对鸟群捕食行为的研究，具有计算简单、收敛速度快、鲁棒性强等优点。在该算法中，待优化问题的潜在解被视为没有体积和重量的运动粒子，共同组成一个粒子群，而每个粒子均可由运动速度和空间位置进行描述。优化时，首先随机生成一个粒子群，然后通过迭代找到最优解。在每一次迭代中，各粒子根据2个极值来更新自身的速度和位置，更新公式如(1)式所示。

(1)

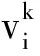
通过基于(1)式的迭代过程，利用粒子群内的信息共享以及粒子个体自身的经验总结来不断修正个体的行为，最终使粒子群聚集于最佳区域，获得问题的最优解。然而，研究和实践证明，PSO不属于全局收敛算法，容易出现“早熟”现象而陷入局部最优。

文化算法是通过模拟人类社会的演进过程而提出的一种双层进化机制，可以显性地获取、保存和利用微观群体演化的知识和经验，图1给出了其模型。由图可见，该算法由群体空间和信念空间组成，两者通过由接受函数accept()和影响函数influence()组成的通信协议进行信息交流。群体空间通过演化操作generate()和性能评价objective()进行自身的迭代求解，并定期通过接受操作accept()将由选取操作select()得到的精英个体作为经验贡献给信念空间，信念空间根据接收到的个体经验通过update()进行自我更新，并定期通过影响操作influence()对群体空间的进一步演化进行指导，上述操作机制使得CA具有了并行演化、相互促进的特点。

图1 文化算法模型

文化算法仅提供了一种进化架构，在求解实际问题之前，还需要在信念空间和群体空间中引入一定的优化算法。本文通过对群体演化类优化算法的详细对比分析，最终确定将前文所述粒子群算法嵌入到2个空间，构建文化粒子群优化算法，利用文化算法的双层进化机制引导粒子群算法的优化过程，提高其全局搜索能力，避免陷入局部最优。

图2给出了所构建文化粒子群算法的流程图。首先，对群体空间与信念空间的粒子个数、最大迭代次数、惯性权重、学习因子等参数进行初始化，计算每个粒子的适应度值，并保存个体和群体的初始极值及其位置。然后，判断是否需要执行接受操作，若不需要，则依据(1)式对群体空间中各粒子的速度和位置进行更新，并计算更新后粒子的适应度以及个体和群体的极值和位置，以备下一次更新使用；若需要执行接受操作，则用群体空间中一定数量的精英个体替换信念空间中相应数量的较差个体，同时依据(1)式对信念空间中各粒子的速度和位置进行更新，并计算更新后粒子的适应度以及个体和群体的极值和位置，以备下一次更新使用，接着判断是否需要执行影响操作，若需要，则用信念空间中一定数量的精英个体替换群体空间中相应数量的较差个体，反之则不做任何操作。上述迭代过程不断重复，直至满足终止条件，即迭代次数超过最大允许值或搜索到的极值达到预定阈值，优化停止，输出最终极值(适应度值)及其空间位置。实际应用中，适应度函数是依据优化目标建立的，而粒子在空间各维度上的坐标便是优化参数，比如在SRM优化中，适应度函数可由效率等建立，而几何尺寸和控制参数等可作为粒子的坐标。另外，需要说明的是，是否需要执行接受或影响操作可通过当前代数对AcceptStep或InfluenceStep求余进行判断，依据图2，若AcceptStep=5，则每对群体空间更新4次便需要执行1次接受操作。

图2 文化粒子群优化算法流程图

为了验证文化粒子群优化算法的可行性，本文利用经典优化问题——压力容器优化设计对算法的性能进行了测试。图3所示为用于存放压缩空气的压力容器，它由两头的锻压半球帽和中间的轧钢圆筒组成，各部件通过焊接连成一个整体。

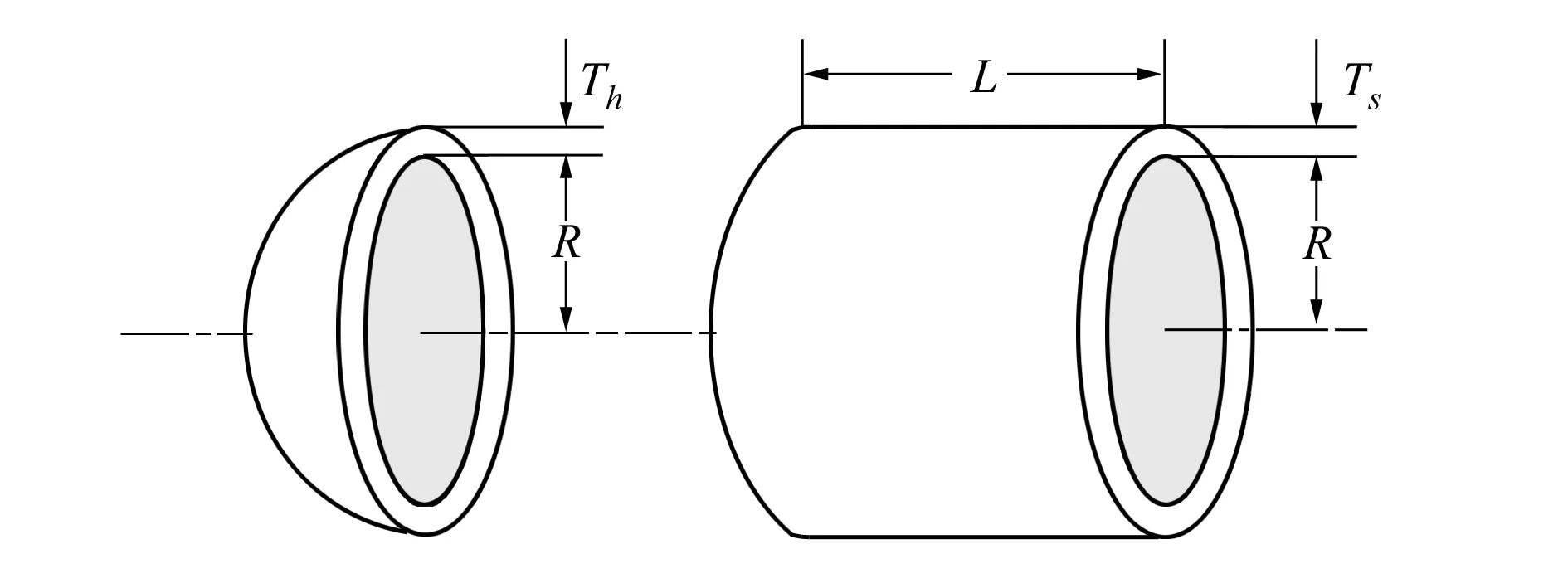
图3 压力容器示意图

以制造成本最小为优化目标，制造成本包括材料、锻造和焊接成本，优化变量为半球帽厚度Th、圆筒厚度Ts、圆筒内半径R和圆筒长度L，而约束条件则遵照美国机械工程师学会(ASME)制定的锅炉和压力标准设置。该优化问题的数学描述如下：

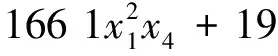
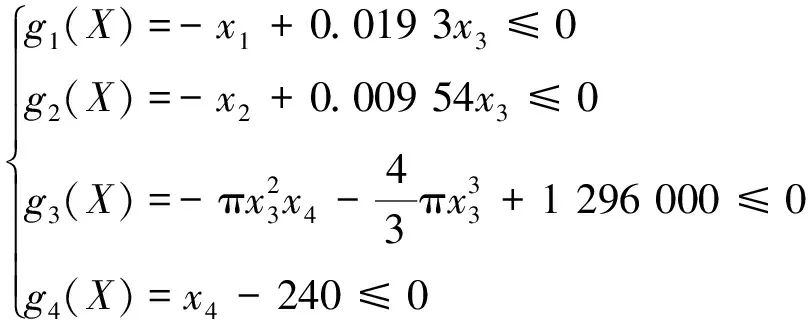
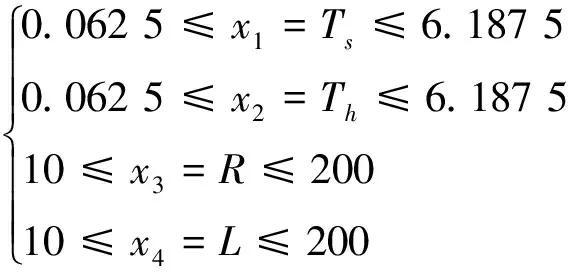
本文在求解该问题时以(2)式作为目标函数，亦即适应度评估函数：

(2)

且，如果g1(X)、g2(X)和g3(X)满足约束条件，则将其设为0，否则保持原值，以达到惩罚的目的。

CPSOA的相关参数取值如下：惯性权重ω=0.729，学习因子c1=c2=1，粒子总个数m=100，最大迭代代数n=500，AcceptStep=5，InfluenceStep= 15，终止条件为迭代次数超过n。

图4给出了优化过程中最大适应度以及各优化变量的变化曲线，可见该算法的收敛速度很快且很稳定，通过优化使得压力容器的制造成本降低至5 654，此时x1=0.75，x2=0.375，x3=40.319 7，x4=199.999 2，证明了该方法的有效性。文献[16]给出了PSO、GPSO(高斯PSO)、PSO-CA和GPSO-CA这4种方法对同一压力容器优化设计问题的求解结果，分别为8 329.490 8、7 781.111 0、6 201.473 7以及6 112.561 9，本文方法优化所得制造成本比这4种方法都要低，从而显示了该方法的性能优势，也证明了参数选取的正确性。

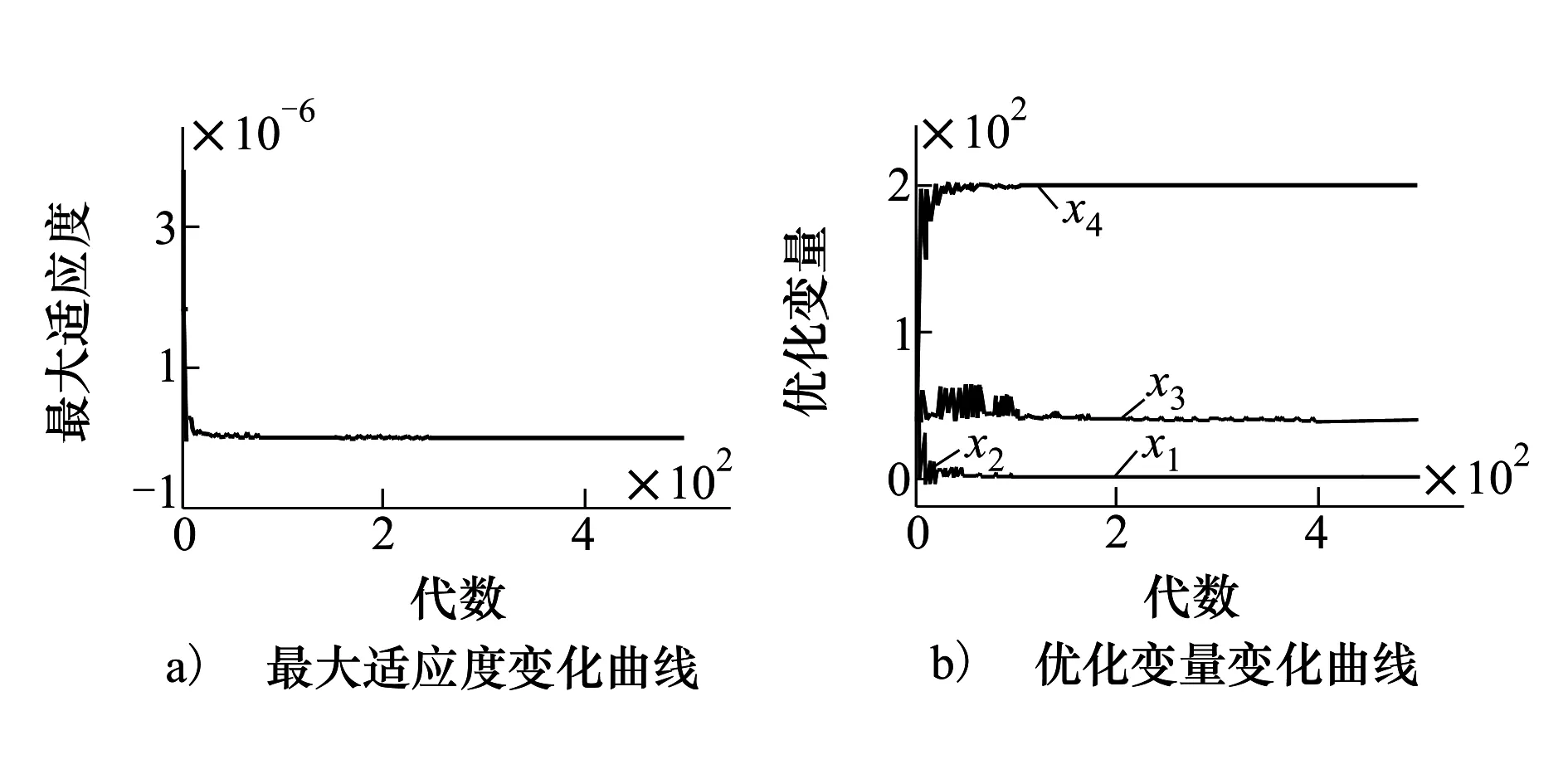
图4 压力容器优化设计结果

2 SRM初始设计

本文利用传统方法对一个三相6/4极SRM进行了初始设计，指标如下：电压Vs=270 V，额定转速n=27 000 r/min，额定功率PN=30 kW，额定效率η=80%。在设计之前，先给出主要尺寸的几何定义，如图5所示。

图5 SRM各主要尺寸示意图

本文的初始设计方法主要基于SRM的输出方程，该方法简单直观，且能很好地反映设计指标与主要尺寸间的关系，具有较好的实用性[17]。(3)式给出了SRM的输出方程。

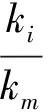
(3)

式中：Dr为转子外径；Lstk为铁心叠长；B为磁负荷，此处取0.4T；A为电负荷，此处取28 000 A/m；ki、km为电流系数，此处取ki/km=0.5/0.8；Pem为电磁功率，可按下式进行估算：

(4)

要求出电机尺寸，还需要引入细长比λ，即λ=Dr/Lstk，对于SRM而言，一个典型取值为λ=1，即Dr=Lstk。

由上述公式可以求出Dr=Lstk=74 mm，则转子外半径rr=74/2=37 mm。利用定、转子外径的比值Dr/Ds可以很方便地求得SRM的定子外径，对于三相6/4极SRM而言，可取Dr/Ds=0.5，进而求得定子外径Ds=148 mm，则定子外半径rs=148/2=74 mm。至此已求出SRM的主要几何尺寸，图5中其他尺寸以及每极相绕组匝数的求取方法可参见文献[17]，最终得到每极相绕组匝数为10。

根据以上计算结果，同时考虑实际加工水平，最终确定了表1所示的尺寸取值。

表1 初始设计SRM几何尺寸取值/mm

本文采用角度位置控制法(APC)对SRM进行控制，其中开通角θon和关断角θoff初始取值如下：

θon=θu=45°

(5)

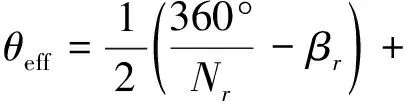
(6)

式中：θu为非对齐状态时转子角位置，记为45°，Nr为转子极数，βr为转子极弧。

本文利用自己研发的SRM性能解析计算软件对方案进行核算，该软件已经过反复考核，证明其计算误差在工程允许范围内，且具有快速、方便等优点。经过核算，可得到在额定转速下，初始设计方案的输出转矩为9.3 Nm，输出功率为26.3 kW，效率为81.4%，转矩脉动系数为1.344 6。可见，初始设计方案的性能基本满足指标要求，不足在于输出功率稍低，效率偏低，且转矩脉动系数较大。

3 SRM多目标优化设计

开关磁阻电机的尺寸参数众多，且与电机性能的关系较为复杂，在进行优化之前，有必要分析它们对电机效率、转矩脉动等的影响模式，进而为优化提供理论依据。在保证电机外形尺寸不变的前提下，经过大量仿真及理论分析发现下列尺寸对电机的效率具有较大影响：定子轭高ys、转子外径rr、定子极弧βs和转子极弧βr。另外，定、转子极弧的取值不仅会影响电机效率，而且会在很大程度上影响转矩脉动。

在上述研究结果基础之上，本文从提高效率、减小转矩脉动的角度出发，对SRM本体的关键尺寸及控制参数进行优化，优化的前提是电机外形尺寸不变，额定功率不小于初始设计方案的26.3 kW。

1) 单目标优化

以效率为优化目标函数，以定转子极弧、转子外径以及定子轭高为优化变量，CPSOA中相关参数的取值与压力容器优化问题相同(下同)。图6给出了优化结果。

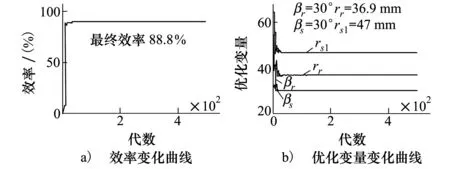
图6 单目标优化结果

由图可见，优化后电机的效率提高为88.8%，且功率大于26.3 kW，满足优化前提，然而转矩波动系数为1.355 3，大于初始设计的1.344 6。需要说明的是，图中的rs1=rs-ys为定子内径。

2) 多目标优化

为了在优化时兼顾电机效率和转矩脉动，将目

标函数设为(7)式。

F(X)=e(k1E+k2/Tr)

(7)

式中：E为效率，k1、k2为系数，其取值可根据优化指标要求以及E和Tr的范围确定，本文中取k1=0.002，k2=1。

图7给出了优化结果，由图可见优化后的目标函数值为2.768 7，此时的电机效率为86.6%，转矩脉动系数为1.183 1。与前文单目标优化结果相比，本次优化在保证电机效率较高的同时，转矩脉动系数有较大减小，两者达到了较好的平衡。

众所周知，开关磁阻电机的性能同时受到结构参数和控制参数的影响，为了得到系统级的最佳设计方案，应该同时对两者进行优化。图8给出了控制参数和几何尺寸综合多目标优化的结果，优化后的目标函数值为11.305 6，此时电机效率为88%，转矩脉动系数为0.444 6。可见，通过综合多目标优化，可以得到比图7所示几何尺寸单一优化性能更好的设计方案。

图7 几何尺寸多目标优化结果 图8 控制参数、几何尺寸综合多目标优化结果

4 结 论

本文针对目前SRM设计依赖传统方法和经验参数、专业化程度高、难以得到全局最优解等现状，采用文化粒子群优化算法对电机进行了优化设计与控制。首先将粒子群算法嵌入到文化算法的群体空间和信念空间，构建了文化粒子群算法，并通过经典的压力容器优化设计问题对算法的有效性和性能优势进行了验证。然后，针对一定的技术指标，利用传统方法对SRM进行了初始设计，得到了叠片几何尺寸、绕组匝数、开通/关断角等的取值。校核结果表明，初始设计方案的效率较低、转矩脉动较大。最后，利用文化粒子群算法对SRM初始设计方案进行了优化，有效提高电机效率的同时，大幅减小了转矩脉动。本文的研究对于SRM优化设计及控制具有一定的参考价值。

参考文献：

[1] Vijayakumar K, Karthikeyan R, Paramasivam S, Arumugam R, Srinivas K N. Switched Reluctance Motor Modelling, Design, Simulation, and Analysis: A Comprehensive Review[J]. IEEE Trans on Magnetics, 2008, 44(12): 4605-4617

[2] Song Shoujun. Detailed Design of a 30 kW Switched Reluctance Starter/Generator System Used in More/All Electric Aircraft[M]. Aachen: Shaker Verlag, 2009

[3] Zhu Z Q, Chan C C. Electrical Machine Topologies and Technologies for Electric, Hybrid, and Fuel Cell Vehicles[C]∥IEEE Vehicle Power and Propulsion Conference, 2008

[4] Cardenas R, Pena R, Perez M, Clare J, Asher G, Wheeler P. Control of a Switched Reluctance Generator for Variable-Speed Wind Energy Applications[J]. IEEE Trans on Energy Conversion, 2005, 20(4): 781-791

[5] Sozer Y, Torrey D A. Optimal Turn-off Angle Control in the Face of Automatic Turn-on Angle Control for Switched-Reluctance Motors[J]. IET Electric Power Applications, 2007, 1(3): 395-401

[6] Wu W, Dunlop J B, Collocott S J, Kalan B A. Design Optimization of a Switched Reluctance Motor by Electromagnetic and Thermal Finite-Element Analysis[J]. IEEE Trans on Magnetics, 2003, 39(5): 3334-3336

[7] Miller T J E. Optimal Design of Switched Reluctance Motors[J]. IEEE Trans on Industrial Electronics, 2002, 49(1): 15-27

[8] Cheshmehbeigi H M, Yari S, Afjei E. Design and Analysis of Low Torque Ripple Switched Reluctance Motor Using 3-Dimensional Finite Element Method[C]∥European Conference on Circuit Theory and Design, 2009, 857-861

[9] Owatchaiphong S, Carstensen C, De R W Doncker. Optimization of Predesign of Switched Reluctance Machines Cross Section Using Genetic Algorithms[C]∥7th International Conference on Power Electronics and Drive Systems, 2007, 707-711

[10] 白凤仙, 邵玉槐, 孙建中. 利用智能型模拟退火算法进行开关磁阻电机磁极几何形状的优化[J]. 中国电机工程学报, 2003, 23(1): 126-131

Bai Fengxian, Shao Yuhuai, Sun Jianzhong. Optimization Design of Pole Shape of SRM by Using Intelligent Simulated Annealing Algorithm[J]. Proceedings of the CSEE, 2003, 23(1): 126-131 (in Chinese)

[11] Kano Y, Kosaka T, Matsui N. Optimum Design Approach for a Two-Phase Switched Reluctance Compressor Drive[J]. IEEE Trans on Industry Applications, 2010, 46(3): 955-964

[12] Raminosoa T, Blunier B, Fodorean D, Miraoui A. Design and Optimization of a Switched Reluctance Motor Driving a Compressor for a PEM Fuel-Cell System for Automotive Applications[J]. IEEE Trans on Industrial Electronics, 2010, 57(9): 2988-2997

[13] Daneshyari M, Yen G G. Constrained Multiple-Swarm Particle Swarm Optimization within a Cultural Framework[J]. IEEE Trans on Systems, Man and Cybernetics, Part A: Systems and Humans, 2012, 42(2): 475-490

[14] 王奕首, 艾景波, 史彦军, 滕弘飞. 文化粒子群优化算法[J]. 大连理工大学学报, 2007, 47(4): 539-544

Wang Yishou, Ai Jingbo, Shi Yanjun, Teng Hongfei. Cultural-Based Particle Swarm Optimization Algorithm[J]. Journal of Dalian University of Technology, 2007, 47(4): 539-544 (in Chinese)

[15] Lin C J, Chen C H, Lin C T. A Hybrid of Cooperative Particle Swarm Optimization and Cultural Algorithm for Neural Fuzzy Networks and Its Prediction Applications[J]. IEEE Trans on Systems, Man and Cybernetics, Part C: Applications and Reviews, 2009, 39(1): 55-68

[16] Dos Santos Coelho L, Mariani V C. An Efficient Particle Swarm Optimization Approach Based on Cultural Algorithm Applied to Mechanical Design[C]∥IEEE Congress on Evolutionary Computation, 2006, 1099-1104

[17] 吴建华. 开关磁阻电机设计与应用[M]. 北京: 机械工业出版社, 2000

Wu Jianhua. Design and Application of Switched Reluctance Machine[M]. Beijing: Mechanical Industry Press, 2000 (in Chinese)