分布式网络中随机接入传送容量的研究

李娜娜，邹东尧，陈昌海

(1．郑州轻工业学院计算机与通信工程学院，河南郑州450002;2． 四川工程职业技术学院电气信息工程系，四川 德阳618000;3．北京邮电大学 泛网无线通信教育部重点实验室，北京100876)

0 引言

自从Gupta 对分布式网络容量［1］进行了创新性的定义之后，人们对分布式网络容量进行大量的研究，其中Weber 做出了尤为重要的贡献． 在文献［2］中，Weber 重新定义了能够用来衡量分布式网络容量的参量，即传输容量(Transmission Capacity，TC)，其被定义为:通信中断概率受限时，网络在单位面积上能够实现的成功通信数量． 由于使用了随机几何理论对分布式网络进行建模，使得人们可以用严格的数学推导得到TC 的上下界，并可以得到TC 在一些特殊情况下的闭合表达式，人们在此基础上可以使用各种传输技术来进行进一步的研究，如多天线［3］，干扰消除［4］，感知技术［5］等．

Weber 的网络模型被认为是分布式网络容量研究中一种最经典的网络模型，使用随机几何理论进行网络建模研究TC 的方法得到了业界的广泛认同．但是这种经典的网络模型同样存在不足，该模型中任意发送机(Transmitter，TX)可以在其最大中继距离Rm内随机选择一个中继接收机(Receiver，RX)进行数据传输，但是这个选择并没有方向性，无法保证数据传输能够最终到达目的RX 处．文献［6］中提出了改进的系统模型，规定了任意TX 需在指向目的接收机方向选择中继RX，并定义了空间进度密度(Spatial Density of Progress，SDP)来衡量分布式网络容量的大小．使用这种改进的网络模型，可以确保中继RX 比TX更接近目的RX，但是需要满足目的RX 位于无穷远处这一假设条件，然而实际中目的RX 却都是位于有限远处的． 文献［7］定义了新的网络模型来试图解决这个问题，规定了目的RX 位于TX 有限远处，在两者之间有等间距的几个固定中继RX 来辅助信息传输，并定义了随机接入传输容量(Random Access Transport Capacity，RATC)来衡量网络容量的大小． 文献［7］突破了近年来局限于单跳网络容量研究的状况，开始尝试对端到端的多跳网络容量进行研究，但是由于中继RX是人为设置好的固定中继，与实际中继RX 随机分布的情况不符，所以没有继续深入的研究成果出现．

基于文献［7］的研究成果，笔者将使用RATC来衡量多跳网络容量的大小，重新定义可用于研究多跳网络容量的网络模型，假定目的RX 位于有限远处，中继RX 随机分布，并提出新的中继RX 选择策略来确保数据经过有限次数中继后能够成功到达目的RX 处．

1 系统模型和参数说明

在一个网络规模没有限制的分布式网络中，所有通信使用相同的频率，同一时隙中TX 的位置在二维平面上服从密度为λ 的泊松点过程(Poisson Point Process，PPP)(Π)分布，则在一个半径为R 的圆形区域内出现k 个TXs 的概率为Pr(k in R)，如式(1)所示．在网络中任意TX 都有唯一一个RX(不属于Π)与之对应，本研究使用编号i 表示由TXi 和RXi 构成的通信对． 使用文献［2］的经典研究方法，把一个参考RX

放在二维坐标的原点，这个参考RX 和它相对应的TX 组成编号记为0(0∉Π)通信对． 由于PPP具有平稳性，所以RX0 处统计特性的研究结果与任意RXi(i≠0)处是一样的，且RX0 处接收到的任意TXi(i ≠0)发送的信号都被认为是干扰信号．

任意TXi 使用固定功率P 发送信号，路径损耗因子为α(α ＞2)，任意TXi 与RXj 之间的小尺度衰落为Hij，TXi 距离RX0 的距离记为Xi，则RX0 处的总干扰信号功率为∑i∈ΠPHijX-αi． 本研究中小尺度衰落为瑞利衰落，其功率衰减因子服从参数为τ 的指数分布． 任意RX 处的信号与干扰功率之比的最低门限要求记为β，TX0 和RX0之间的距离(也可以叫中继传输距离)记为R，则RX0 处的中断概率为q(l)，如式(2)所示．其中，Π 如式(3)所示．

定义源TX 和目的RX 之间距离为L，且源TX 无法将数据直接发送到目的RX，需要经过多次中继传输，任意一次中继传输的最大中继距离为Rm．图1 为中继RX 选择区域示意图，如图1 所示，节点A 为一次中继传输中的TX，节点C 为目的RX，则AC≤L;图中扇形阴影部分为TX 的中继RX 选择区域，此区域有3 个因素决定:扇形区域的中轴线为指向目的节点C 方向，扇形的半径Rm表示一次中继传输的最大距离，角度θ 限定了中继RX 选择的角度范围为［-θ，θ］．

在多跳传输中，除最后一跳外，中继RX 使用随机选择策略，则中继传输距离R 的概率密度公式为fR(r)，如式(4)所示． 当数据到达节点距离目的节点的距离小于Rm时，数据能直接传输到目的节点，定义这一跳为最后一跳，即

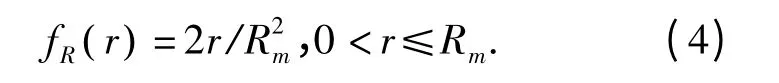
图1 中继RX 选择区域Fig．1 The region for the selection of relay RX

目的节点作为数据的接收节点，且假定传输必定成功．最后一跳的设定可以在最大程度上保证数据在有限跳数内被传送到目的节点，并且可以避免令人尴尬的情况出现，即数据已经到达目的节点附近，还不断选择目的节点附近的其它节点进行中继传输．

分布式网络容量的研究都是基于中断概率受限这一前提，最大中断概率记为ε，令q( λ) =ε 可以求得对应于ε 的最大TX 密度λε，参考文献［7］中随机接入传送容量的定义，网络的随机接入传送容量可以被定义为

2 随机接入传送容量的研究

2．1 中继RX 选择区域的的进一步定义

图1 所定义的中继RX 选择区域给出了对于角度θ 的约束条件，即θ≤∠DAC．但是，每一次中继传输时TX 与目的RX 之间的距离都会发生变化，∠DAC 的大小也会随之变化，所以还需要进一步明确角度θ 的约束条件．

定理1:在分布式网络中，当目的RX 位于有限远处L(L ＞Rm)时，定义由最大传输距离Rm和角度范围［-θ，θ］确定的指向目的RX 的扇形中继RX 选择区域，当θ≤π/3 时，数据能够在有限跳数内传送到目的RX．

证明:笔者的研究基于L ＞Rm这一条件，此时源TX 无法直接把数据发送到目的RX，需要选择中继传输． 如图1 所示，以目的节点C 为圆心且以线段AC 长为半径画圆，并与以TX 为圆心且以最大传输距离Rm为半径所画的圆相交与D，则由两圆相交区域所确定的最大中继RX 选择区域如图1 中阴影部分所示，此时θ =∠DAC，为最大值，实际中只要满足公式(6)的约束条件就可以．从目的节点C 向AD 做垂直线并交AD 与F 点，则由三角函数的定义可以得到式(7)．

以节点C 为圆心且Rm为半径画圆交AC 与点B，当节点A→B 时，有AC→Rm，根据公式(7)可以得到∠DAC→π/3，此时∠DAC 取最小值，结合公式(6)可以得到θ≤π/3，证明完毕．

综上所述，角度θ≤π/3 时，数据能在有限跳数内从源TX 发送到目的RX，中继RX 选择区域的角度范围为［-θ，θ］．

2．2 随机接入传送容量的数学推导

本节将在定理1 所定义的中继RX 选择区域基础上进行随机接入传送容量的公式推导．

当中继距离R=r 时，中断概率的公式(2)经过变换可以得到式(8)． 因为功率衰减因子服从参数为τ 的指数分布，则可得到式(9)．结合公式(8)和(9)可以得到式(10)．其中LIΠ(* )是IΠ的概率密度函数的拉普拉斯变换． 使用与文献［8］中附录相似的证明过程可以得到式(11)．

式中:γ = 2/α．

由于H 服从参数为τ 的指数分布，因此，

把Γ(1 + γ)Γ(1 + γ)= γπcsc(γπ)和式(12)代入公式(11)可以得到式(13)． 把式(13)代入式(10)可以得到当中继距离R = r 时的中断概率表达式q(λ| R = r)如式(14)所示．结合式(4)和(14)可以得到网络的中断概率q(λ)，如式(15)所示．

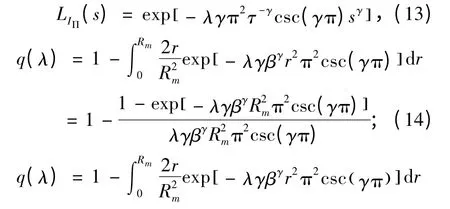
令q(λ)=ε，利用公式(15)可以求得对应于最大中断概率ε 时的最大TX 密度λε如式(16)所示．其中ProductLog(* )是函数f(x)=xex的反函数，且δ =1/(1 - ε)． 最后，把式(16)代入式(5)，可以得到随机接入传送容量C 的数学表达式．

3 仿真和性能分析

这一节中，当没有额外说明时，仿真参数设置为Rm=20 m，β=3，α=4，θ=

图2 是随机接入传送容量C 相对于最大中断概率ε 的曲线图．如图所示，随机接入传送容量随着最大中断概率ε 的增加而增大． 这是因为C的大小主要取决于由式(16)所确定的对应于ε最大TX 密度λε和中继传输的成功概率(1 -ε)的乘积，当ε 增大时，TX 密度λε变大，成功概率(1 -ε)变小，可是(1 -ε)变小的速度没有λε变大的速度快，最终导致了随机接入传送容量C 的增加．ε 增大时TX 密度λε会随之增加，会使得系统内的干扰信号功率增加，最终导致C 的增加变得缓慢．

图2 随机接入传送容量C 相对于最大中断概率ε 曲线图Fig．2 The random access transport capacity C versus ε the maximum probability of outage

4 结论

定义了新的网络模型，可以用于研究分布式网络中端到端的多跳网络容量，并对中继次数和随机接入传送容量进行了理论推导和仿真分析．但是本研究还不够深入，如中继RX 选择区域中角度θ 对网络性能的影响，多天线和干扰消除技术对多跳网络容量的影响等，这些都还需要继续研究．

［1］ GUPTA P，KUMAR P R． The capacity of wireless networks［J］． IEEE Transactions on Information Theory，2000，46(2):388 -404．

［2］ WEBER S，YANG X，ANDREWS J G，et al． Transmission capacity of wireless ad hoc networks with outage constraints［J］． IEEE Transactions on Information Theory，2005，51(12):4091 -4102．

［3］ RAHUL V，ROBERT W H． Transmission capacity of ad-hoc networks with multiple antennas using transmit stream adaptation and interference cancellation［J］．IEEE Transactions on Information theory，2012，58(2):780 -792．

［4］ LEE J，JEFFREY G A，HONG D． Spectrum-sharing transmission capacity with interference cancellation［J］． IEEE Transactions on Communications，2013，61(1):76 -86．

［5］ YIN Chang-chuan，GAO Long，LIU Tie，et al． Transmission capacities for overlaid wireless ad hoc networks with outage constraints［C］． IEEE International Conference on Communications，Dresden:IEEE Press，2009:1 -5．

［6］ LI Di，YIN Chang-chuan，CHEN Chang-hai． A selection region based routing protocol for random mobile Ad Hoc networks with Directional Antennas［C］．Global Telecommunications conference，Miami，FL:IEEE Press，2010:104 -108．

［7］ JEFFREY G A，STEVEN W，MARIOS K，et al． Random access transport capacity［J］． IEEE Transactions on Wireless Communications，2010，9(6):849-856．

［8］ SOUSA E S，SILVESTEI J A． Optimum transmission ranges in a direct-sequence spread-spetrum multihop packet radio network［J］，IEEE Journal on Selected Areas in Communications，1990，8(5):762 -771．