基于辅助函数思想的城市高压电网无功优化

2014-03-25周晓娟王奎英

郑州大学学报（工学版） 2014年4期

周晓娟，王奎英，张将

(1．河南机电职业学院电子工程系，河南郑州451191;2．重庆大学电气工程学院，重庆400044)

0 引言

电力系统的经济运行，实质上是一个最优化问题．从运筹学角度来讲，就是在满足一定的约束条件下，使得目标函数达到最优．按照优化对象，可分为发电机组的最佳开停、电源功率的最优分布和无功电源的最优补偿等．优化的目标函数也因对象的不同而不同，如发电费用最小、网损最小、无功补偿容量最小和综合经济效益最大等．

电力系统无功优化［1］是通过改变无功潮流在网络中的分布来达到降低网损，保证电压质量的目的．无功优化的方法通常分为两种，即经典式和现代启发式．这些方法在计算速度、实用范围、收敛性和对初值要求等方面都各有特点．如何实现优化问题中离散变量和连续变量的综合处理、保证算法收敛性和对非线性函数的处理是目前无功优化需要考虑的焦点问题［2］．

鉴于电容器组的离散特性，笔者采用了一种简单实用的处理方式［3］．构造一个表示电容器组投切状态的辅助函数，将离散变量转化为连续变量．设定电容器状态初始值为0．5，一旦新计算的状态值偏离0．5，则把新计算出的值作为电容器组的当前投切状态值，电容器组投切状态值最终以整数0(退出)或者1(投入)输出．

1 电容器的处理

电容器的投切具有离散的特性，在传统最优化问题求解中，混合整数规划方法对解决离散变量非常有效．它为了逐渐逼近全局的最优解，采用分支定界来不断地缩小可行域．这种算法存在一定的缺陷性，如果计算维数不断增加，计算时间也会跟着急剧增加，有时甚至是爆炸性的．为了避免上述问题出现，引入变量Km，Km的取值范围是0 ～1 的一个实数，用它表示电容器投切状态．构造一个关于它的辅助函数y(Km)如图1 所示．

图1 函数曲线Fig．1 Function curve

辅助函数y(Km)为

y = (Km-0．5)2+5． (1)

ya= max y = max［(Km-0．5)2+5］． (2)

对于y 取得最大值ya时，Km值选取如下．

(1)当0 ≤Km＜0．5 时，Km值取0，表示退出该电容器．

(2)当0．5 ＜Km≤1 时，Km值取1，表示投入该电容器．

2 优化模型

无功优化的目标函数［4］我们可以用当前时刻的最小网损来表示．所有发电机的有功出力在不考虑平衡节点的情况下，可以认为是给定不变的．对于一定的负荷来讲，平衡节点的注入功率将会伴随着网络损耗的变化而发生变化，因此系统总网损最小可以用平衡点有功注入最小来表示．

2．1 无功优化的目标函数

笔者以包括全网电能损耗和控制设备的调节代价的综合费用最小作为无功优化调度的目标函数．在只考虑电容器的情况下，目标函数表达式如下．

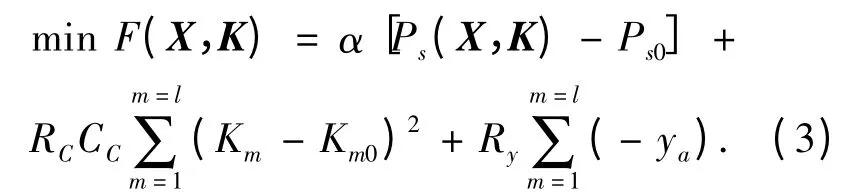
式中:向量X 由直角坐标形式的节点电压的实部和虚部表示(Xi= ei+ jfi);α 为综合电价(元/kWh)，α 取值为0．5 元/kWh;Ps(X，K)，Ps0分别是单一时段优化后和优化前全网的有功损耗(用平衡点的有功功率来表达);CC为单位调节代价(元/ 次)，根据现场人员提供的经验数据取值为2 元/ 次;RC为权重系数，它的取值范围为0 ～1，为了改善迭代收敛特性，RC在迭代刚开始时取较小值，随着迭代次数的逐渐增加，RC也逐渐增加，最后增加到1;Ry取值为1 元;Km0为电容器组的初始状态值．

2．2 无功优化目标函数的约束条件

2．2．1 等式约束

等式约束条件为潮流计算中的节点功率平衡方程:

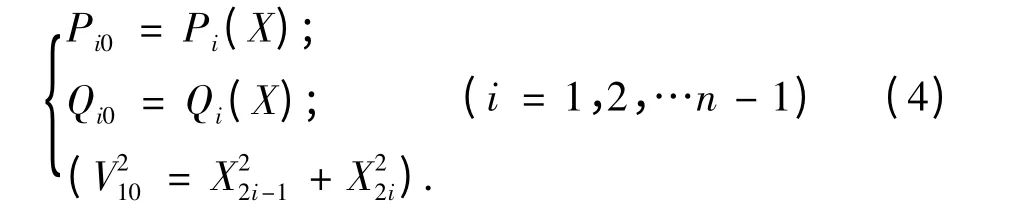
式中:Pi0、Qi0、Vi0分别为节点有功功率、无功功率和电压的给定量;n 为系统的总节点数;X2i-1和X2i为直角坐标形式下节点i 电压的实部和虚部;当为PV 节点时，可用式(4)中的电压方程代替无功等式约束．

2．2．2 不等式约束

电容器状态Km约束0 ≤Km≤1(m = 1，2，…l)． (5)

并联电容器组数约束0 ≤Cl≤Cls(l ∈T)．(6)

支路功率约束Pij(X)≤Pijmax． (7)

节点电压约束Vimin≤Vi≤Vimax，(i = 1，2，…n)． (8)

式中:Km为电容器的投切状态;Cl为节点l 处所安装的电容器组数;Cls为节点l 安装的最大电容器组数;Pijmax为i - j 支路有功功率的最大输送值;Vimin、Vimax分别为节点i 的电压上下界．

3 无功优化问题的最优求解

3．1 增广目标函数

根据最优潮流计算中的梯度法［5］，将目标函数写成如下形式．

式中:λi，mi分别表示有功无功的拉格朗日乘子;wtk，rgp分别是电容器状态约束和支路功率约束的罚因子;cox 表示越界负荷节点电压下标的集合;cop 表示越界支路功率下标的集合;cok 表示越界电容器投切状态下标的集合．

根据最优潮流可知，目标函数极小值的必要条件为

为方便起见，对于式(10)中的节点功率约束，可用hi(X，K)= 0 来表示．其中，∂Ps/∂XN为将潮流计算中的雅可比矩阵扩展到包含平衡节点时有功功率对应行中的元素．

别为节点直角坐标形式下电压的实部和虚部．

3．2 一维搜索

用黄金分割搜索法［6］(即0．618 法)，对目标函数进行一维搜索．直到收敛条件满足才停止搜索．否则，就要建立H-k到H-k+1的迭代关系，其中H-k的初值取单位矩阵．

对于目标函数，可以简化为e ，K )+ W(Z，V)． (11)

其中，W(Z，V)表示所有不等式约束．

由变尺度法可知

Δ gk= ［∇XC(Xk+1，Kk+1，λk+1)- ∇XC(Xk，Kk，λk)］+［∇KC(Xk+1，Kk+1，λk+1)- ∇KC(Xk，Kk，λk+1)］． (12)

经化简可得

Δ gk= 2ruX(Xk+1-Xk)+2(Kk+1-Kk)(wK+RCCC-1)+∑n-1i=1λi［J'k+1- J'k］． (13)

变量的增量表达式如下:

Δx = ［Xk+1- Xk，Kk+1- Kk］． (14)

ηk= θΔ gk+ (1 - θ)H-kΔ xk(0 ＜θ ＜1)．(15)

同时，对θk的选择应该遵循下式:

在已知ηk，Δ Gk，θ，Δ XK的前提下，即可得到变尺度矩阵的迭代关系式．

4 算例分析

算例为试运行系统，我们用系统I 来表示，如图2 所示．系统I 在文中所用的当前系统运行方式下，经过节点的压缩等过程，共得到3 个子系

图2 110 kV 系统IFig．2 110 kV power system I

统，第1 个子系统中含有30 个节点，5 台电容器组，2 台双绕组变压器，4 台三绕组变压器．第3 个子系统含有3 个节点，1 台电容器组，1 台双绕组变压器．其中只有第1 个子系统代表系统I 主运行方式．电容器编号依次为C1-卫1，C2-孝1，C3-孝2，C4-崔容18 外，C5-崔容18，C6-樊2，C7-樊1．

表1 系统I 电容器优化结果Tab．1 Capacitor optimization results in power system I

在110 kV 系统I 的子系统1 中，一共有五台电容器组，分别为C2，C4，C5，C6，C7，其中C4没有投入运行．运用Fortran 语言进行编程，程序运行结果给出了优化后各电容器组的投切状态．表1 列出了电容器组状态;表2 给出了优化前后的有功损耗．通过程序计算我们得出了优化前的有功损耗为11．512 07 MW，优化后的有功网损为11．503 96 MW;优化前的综合费用为0．601 7 万元，优化后的费用为0．598 6 万元，可节省0．003 1 万元．