基于半监督聚类理论的MQAM 信号的调制识别

孙刚灿，李苹苹，申金媛，赵海东

(郑州大学 信息工程学院，河南 郑州450001)

0 引言

通信信号调制方式的识别是信号分析的重要部分，也是软件无线电的关键技术［1］，在军用和民用上均有广泛运用． 对于MQAM(Multiple Quadrature Amplitude Modulation)信号，理论上调制阶数可以很大，调制星座图的样式可以有任意多种．因此往往很难确定待识别信号调制方式的可能范围［2］．由于MQAM 信号调制方式同时进行了幅度和相位的调制，而任何一种数字幅相调制信号都可以用唯一的星座图表示［3］，因此可以用星座图聚类方法解决本问题．

最常用的传统聚类算法是模糊C -均值算法及其改进算法［4］．模糊C -均值算法需要预先知道初始聚类中心的数目及位置，因此初始聚类中心的选择对聚类结果有着很大的影响． 而半监督聚类的方法是指面对大量的无标记数据，给出属于各个聚类的一些标记数据，从而指导聚类的结果向着高精确度的方向发展［5］． 笔者采用半监督聚类的方法，基于减法聚类中“密度”的思想，选出部分“密度”较大的数据点作为标记点［6］，来指导聚类中心的选择，进而减少算法的迭代次数．另外，修正了误差平方和函数的更新公式，使迭代过程中误差平方和函数曲线趋于平滑．

由于传统的减法聚类对不同阶数的调制信号的聚类效果不同，不同阶数的调制信号要求的领域半径值不同［1］． 当领域半径值较大时，高阶调制信号的分离性差，而当领域半径值较小时，低阶调制信号的聚合性差． 因此我们提出基于信噪比的自适应减法聚类．

1 基于信噪比的自适应减法聚类算法

对不同阶调制信号自适应设定不同大小的“密度”半径值γa和γb，就能实现星座点初始聚类．考虑N 个码元同步复信号(r1，r2，…，rN)，不失一般性，对其进行幅度归一化得rn，k． 由于每个数据都是聚类中心的候选者，因此rn，k处密度指标Dk定义为

式中:SNR 表示信噪比值;γa(SNR)定义了基于信噪比的密度指标领域，是平均功率意义上的平均噪声幅度值;Ka表示一个性能调整系数，通过调整Ka的取值找到聚类密度领域与平均噪声幅度的比例关系，通过实验给出Ka的合适取值．令γa

(SNR)=Pn，代入(1)式可得

其中，Pn代表了平均每个符号的噪声功率．

在计算每个数据点密度指标后，选择具有最高密度指标的数据点为第一个聚类中心，令rnc，1为选中的点，Dnc，1为其密度指标．每个数据点的密度指标重新修正为

式中:Kb是个常数，其物理意义是密度指标显著减小的领域半径的调整系数，为避免出现相距很近的聚类中心，一般选Kb=1．5Ka． 通过迭代操作，可以逐渐求出密度最大点，但是不能确定密度最大点的数目，因此需要定义一个聚类结束半径γc，由信噪比大小确定=Pn．

设已找到的L 个密度最大点聚类中心为rnc={rnc，1，rnc，2，…，rnc，L}，当计算出第L +1 个密度最大点rnc，L+1，然后判断该点是一个新的聚类中心，还是属于已有的聚类，判断公式如下

公式(5)左边表示新的密度最大点与所有已选出的聚类中心点距离平方的最小值，右边为符号噪声的平均功率，常数Kc为调整系数． 通过自适应减法聚类将密度最大的点选出来，为了更好地聚类，将这些点作为标记样本，进而用半监督聚类的思想来指导聚类中心的选择．

笔者先基于减法聚类算法，计算出密度较大的点(将此部分点作为初始聚类中心)通过半监督的思想标记部分优选的样本点，并计算出标记样本点的初始隶属度值，进而更新聚类中心，指导聚类中心的选择，并对FCM 聚类(Fuzzy c-means clustering)算法目标函数进行修改［7］．

2 半监督模糊聚类算法

传统的模糊C 均值聚类算法，迭代收敛比较慢，而且聚类过程中聚类的代价函数值出现了起伏［8］，因此笔者提出了半监督模糊聚类算法．

半监督模糊聚类的关键是用标记样本引导聚类中心的选择［4，9］．在减法聚类的基础上，先通过减法聚类计算出密度较大的点(即初始聚类中心)，将这些点及其周围的点作为标记样本点，进而优化迭代的过程．设N 个码元同步复信号组成的样本集合R={r1，r2，…rN}，mi为聚类中心，uik

是第k 个样本对于第i 个聚类的隶属度函数． 用以下公式选择密度较大点的周围的点

Ku是常数用来调整密度较大点周围点数的选择，P1n是归一化后的信号噪声功率． 对这部分标记的样本点计算初始的隶属度值(未标记样本点fik值为0)，以矩阵F=［fik］给出i=1，2，…，C，k=1，2，…，N．其中C 代表聚类中心数目，N 代表标记的样本点数．由如下公式计算fik．

接下来开始循环迭代过程，对所有样本点按公式(8)计算其隶属度uik

由隶属度的物理意义可知，一个样本对各聚类中心的隶属度之和为1，即

其中标记样本的隶属度更新公式如(10)所示

公式(7)，(8)中的b 是控制模糊程度的常数，当b取2．3 时效果较好，当b 趋向1 时，算法变成硬聚类．当b 趋向无穷时，算法的聚类结果是最模糊的，即b 的取值影响聚类的模糊度．隶属度更新完后，按下式更新聚类中心．

当隶属度和聚类中心都更新完之后，将得到的隶属度和聚类中心代入误差平方和函数计算［10］．误差平方和函数的计算公式如下

公式(10)，(12)中α 可理解为对标记样本的可信度，标记的样本点越多，α 值就越小，可信度越低． 相反标记的样本点越少，α 值就越大，可信度就越高，由此可知，通过标记样本点的多少来指导隶属度的更新，进而指导聚类过程．通过数次迭代，使聚类的代价函数逐渐收敛，迭代的收敛条件如下

Je(k+1)=Je(k)． (13)

通过上述标记的样本点指导隶属度和聚类中心的更新，使算法收敛快、聚类精度高．

3 基于半监督模糊聚类重构星座图的特征参数提取

由MQAM 信号的基本特征可知不同阶数的调制信号，其有效的聚类中心数不同，因此将半监督模糊聚类和SVM(Support Vector Machine)联合来完成MQAM 信号的调制识别．首先需要提取特征参数［11］，因为不同调制阶数的信号，其有效的聚类中心数是不同的，所以根据聚类中心计算有效性函数值MC，不同阶数的调制信号具有不同的有效性函数值［12］，将MC值作为SVM 的输入，通过SVM 分类器从而可以将不同的调制信号识别出来．求解MC值的过程如下．

(1)先对每个信号xi，计算MCj(i)值．

式中:a(i)为第i 个信号点xi与划分到其所在的聚类中心vj中其它信号点的平均距离;b(i，k)为第i个信号点xi与其它所有划分到第k 个聚类中心vk(k=1，2，…，C，k≠i)的所有信号点的平均距离．

(2)计算第j 个聚类中心vj中所有信号点MCj(i)的平均值MCj．

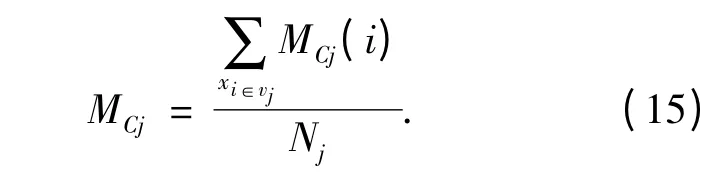
式中:Nj是所有隶属于聚类中心vj的样本点数目．

(3)当聚类中心数为C 时，将所有MCj的均值定义为聚类整体划分结果的有效值MC，

不同阶数的调制信号，将其划分为C 类的有效性程度是不同的，即阶数不同的调制信号的MC值是不同的，因此可以将MC值作为支持向量机的输入特征值，通过SVM 支持向量机将不同阶数的调制信号识别出来．

3．1 支持向量机分类器的设计

支持向量机是基于统计学习的理论发展起来的模式识别方法［13］，在理论上实现了不同类别的最优分类．笔者是在半监督模糊聚类的基础上提取(信号误码率为15%时)特征参数值作为支持向量机分类器的输入，来训练支持向量机分类器．

线性可分情况下，SVM 可以用来求解最优分类面的问题．最优分类面就是要求分类平面不但能将两类样本无误的分开，而且要使两类之间的距离最大．对于两类可分问题，其目标函数为

其中{(x1，y1)，(x2，y2)，…，(xl，yl)，y∈{-1，+1}}是训练集，K(xi，xj)是核函数，Q 是惩罚因子．求解(17)式得到最优解α*=，，…)选择α*的一个正分量0≤≤Q，并计算

由上述可以求决策函数:

笔者先利用半监督模糊聚类重构星座图的方法提取特征参数，然后将特征参数输入支持向量机进行训练．支持向量机在识别多类问题时，常用的方法就是一对一类或一对余类两种算法． 由于前两种算法的运算复杂度高，笔者用分级的思想设计分类器，分16 QAM、32 QAM、64 QAM 3 种信号，实现流程如图1 所示．

用分级的思想设计分类器，首先将提取的特征参数M16输入第1 个16 阶分类器，此时如果输出16 QAM 信号就判为16 QAM，如果输出非16 QAM 信号，将计算非16 QAM 信号的M32输入第2个32 阶分类器，输出32 QAM 和64 QAM 信号，判决结束，3 种信号都识别出来．

图1 SVM 分级的分类器Fig．1 SVM hierarchical classifier

4 仿真结果及性能分析

4．1 重构信号星座图

分别用模糊C 均值和半监督模糊C 均值在误码率为15%时对16QAM 信号的聚类星座图．如图2，图3 所示． 这是对4 000 个样本点进行仿真，图中叉号代表接收到的已加入噪声的复信号序列，圆圈代表实际的星座图，米字星号为减法聚类给出的聚类中心，圆点表示聚类过程，三角形表示最终的聚类结果． 模糊C 均值聚类，初始聚类中心是通过减法聚类计算密度较大的点，由噪声功率的大小设置判决结束门限，从而确定初始聚类中心的数目．但是，这种方法可能会使初始聚类中心数目不准确，如图2 所示，聚类中心数目为17，多于实际的调制星座点数目，而且有些聚类是从两个方向向聚类中心靠近，这可能是隶属度的更新没有监督，更新尺度过大造成的．半监督模糊聚类是通过标记部分密度较大的点，给这些标记的点赋予初始隶属度值，因此，这些点在隶属度更新时与无标记点的权重不同进而来指导隶属度及聚类中心的更新，由图3 可以看出，聚类中心由一个方向向着调制星座点逐渐靠近，最终都聚在调制星座点上，聚类点数为16，聚类中心数目和实际调制星座点数目相同．

图2 模糊C 均值聚类16 QAM 信号聚类星座图Fig．2 Fuzzy c-mean clustering constellations of 16 QAM signals for 16 QAM signals constellation diagram

图3 半监督模糊C 均值聚类16 QAM 信号聚类星座图Fig．3 Semi-supervised fuzzy c-mean clustering

4．2 误差平方和函数曲线

图4 是模糊C 均值算法和半监督模糊C 均值算法的代价函数曲线．从图中看出，上面的那条实线是模糊C 均值算法的代价函数曲线Je随迭代次数增加逐渐减小，迭代50 次时才逐渐收敛而且代价函数的值出现了起伏，原因可能是隶属度更新尺度过大，和图2 中聚类过程从两个方向逐渐向聚类中心靠近的结果相照应． 下面的那条虚线是半监督模糊C 均值聚类算法的代价函数曲线．由曲线看出，随着迭代次数增加代价函数Je逐渐减小，迭代到13 次时就已经收敛．曲线比较平滑，没有出现起伏，这和图3 中聚类过程从一个方向逐渐向调制星座点靠近相吻合．通过上述对比，可以看出通过半监督标记部分样本点指导隶属度和聚类中心的更新，算法的迭代次数少，聚类点数准确、精确度高．

图4 模糊C 均值算法和半监督模糊C 均值算法的代价函数Je曲线Fig．4 Cost function of fuzzy c-means algorithm and semi-supervised fuzzy c-means clustering algorithm Je

4．3 用SVM 分类器进行分类

笔者仿真了16 QAM、32 QAM、64 QAM 3 种调制信号，在误码率为15%的情况下进行实验，每种情况下各实验100 次，得到正确识别率的统计，结果如表1 所示．

表1 SVM 对MQAM 信号的识别率Tab．1 The recognition rate of MQAM signals based on SVM %

由表1 可知通过支持向量机进行分类识别时，首先识别出16QAM 信号且识别率为92%，然后再通过32 阶分类器识别非16 阶信号(包含32阶信号和64 阶信号)． 通过32 阶分类器对32 阶信号的识别率是99%，对64 阶信号的识别率是100%，那么最终的识别率是16 阶信号92%，32阶信号96%，64 阶信号97%．

5 结论

笔者用减法聚类找出密度较大的点，将之作为标记样本．用半监督模糊聚类的方法为标记样本隶属度赋初始值，进而用标记的样本点来指导聚类中心的更新，减少了迭代次数．通过重构星座图来提取特征参数，运用SVM 分类器进行识别，通过实验可以看出对MQAM 信号的识别率大于90%．但是笔者用半监督的思想通过标记部分优选的样本点来指导聚类中心的更新，如果标记的样本点不典型或者标记点错误，将会出现错误聚类的点，造成聚类失败．

［1］ 孙刚灿．非协作数字通信信号调制方式识别算法研究［D］． 北京:北京理工大学信息与电子学院，2008．

［2］ 贺涛． 数字通信信号调制识别若干新问题研究［D］．成都:电子科技大学电子工程学院，2007．

［3］ 王建新，张路平．MQAM 信号调制方式盲识别［J］．电子与信息学报，2011，33(2):332 -336．

［4］ 刘方．数据挖掘中半监督K_均值聚类算法的研究与改进［D］． 吉林:吉林大学计算机科学与技术学院，2010．

［5］ 李春芳，庞雅静，钱丽璞，等．半监督FCM 聚类算法目标函数研究［J］． 计算机工程与应用，2009，45(14):128 -135．

［6］ 张亮，李敏强． 半监督聚类中基于密度的约束扩展方法［J］．计算机工程，2008，34(10):13 -15．

［7］ COVÕES T F，HRUSCHKA E R，GHOSH J． A study of k-means-based algorithms for constrained clustering［J］． Intelligent Data Analysis，2013，17(3):485-505．

［8］ GU Lei，LU Xian-ling． Semi-supervised Localityweight Fuzzy C-Means Clustering:International Conference on System Science［C］//Engineering Design and ManufacturingInformatization． Wuxi，2012:88-91．

［9］ 李昆仑，铮曹，曹丽苹，等．半监督聚类的若干新进展［J］． 模式识别与人工智能，2009，22(5):735-742．

［10］ GARIBALDI D T C L． A Comparison of DistancebasedSemi-Supervised［C］//IEEE International Conference on Fuzzy System． Taipei，Taiwan，2011:1580-1586．

［11］刘爱声．数字通信信号调制识别研究［D］．南京:南京邮电大学，2012．

［12］ CHEN C． A semi-supervised feature selection method using a nonparametric technique with pairwise instance constraints ［J］． Journal of Information Science，2013，39(3):359 -371．

［13］龚晓洁．基于支持向量机的调制方式识别算法的研究［D］．南京:南京邮电大学通信工程系，2011．