螺旋内肋管换热及流体流动数值研究

靳遵龙，赵金阳，王永庆

(1．郑州大学 化工与能源学院，河南 郑州450001;2．洛阳双瑞特种装备有限公司，河南 洛阳471003)

0 引言

内螺纹管是一种在管内壁上设置螺旋型螺纹的高效无源强化换热管． 当流体在内螺纹管管内流动时，在近似轴向周期性螺纹突起的作用下，流体产生周期性的旋转扰动，有利于减薄边界层，降低边界层传热热阻，改善了速度场与热流场的协同程度．在近壁面附近，边界层热阻占总传热热阻的70%［1］．因此，流体旋转扰动所造成的边界层减薄降低了传热热阻．并且，管内的螺纹突起使流体产生流动脱离区，形成湍流漩涡，从而强化了传热．

国内外许多研究者对内螺纹强化换热管进行了卓有成效的研究．但是，由于所研究的内螺纹管的材质、结构参数、加工方法及研究手段的不同，所得结论也不尽相同．Lixin Cheng 等［2］通过实验证实，内螺纹管的传热系数是对应光管的1．2 至1．6 倍，压力损失是对应光管的1．4 至1．7 倍，并给出了内螺纹管的努赛尔数及阻力系数关联式．Wentao Ji 等［3］在假设强化系数为1 的基础上，依据Gnielinski 公式［4］，推导出了Gnielinski 扩展公式，用来预测内螺纹管强化传热． 刘湘云等［5］用实验手段研究了内肋管不同肋高及不同肋条数对管内流体流动与换热特性的影响． 以上众多研究较多采用实验手段，很难获得管内流体流动及换热的细观信息． 笔者采用数值方法，利用CFD 技术，对不同螺距、螺旋角和肋高等27 组结构进行数值研究，详细分析了各个结构参数对流体流动及换热的影响，并以研究结果为基础，拟合了内螺纹管换热及阻力性能公式，同时对强化管综合性能做出评价．

1 物理及数学模型

1．1 物理模型

从物理结构上看，内螺纹管管内流道呈周期性变化．建模时可利用周期性结构计算模型进行简化．当管内流体流动进入充分发展阶段以后，流体流动与换热均以若干个几何周期为变化规律在主流方向上重复． 沿管内流体流动方向可以划分为进口段、周期性充分发展段和出口段．管内流体流动大部分处于周期性充分发展段，该段的流体流动和换热性能，很大程度上反应了内螺纹强化管的基本性能．

笔者充分利用内螺纹管的这种特殊结构，在流体流动充分发展段选取其中的一个螺距长度，作为周期性全截面计算模型进行数值求解． 直观的周期性全截面物理模型如图1 所示． 其中:螺距为10 ～25 mm;肋高为0．5 ～1．2 mm;螺旋角为70 ～85 ℃．

图1 周期性全截面物理模型Fig．1 The periodic physical model

1．2 数学模型及边界条件

计算时假定流体不可压缩、定常流动并忽略重力的影响．将连续方程连同动量方程、能量方程构成可用来求解湍流流动与换热问题的封闭的控制方程组［6］，湍流计算模型采用目前使用最为广泛的标准k-ε 两方程模型． 管内流动工质为水，入口温度为300 K，设置恒定外壁面温度为400 K．采用速度入口以及压力出口边界条件．雷诺数Re 在15 000 ～25 000 之间．

采用有限体积法将计算区域划分成网格，离散格式采用二阶迎风格式．为了提高计算精度，采用结构化六面体网络，由于内壁面上存在螺旋内肋，给网格划分带来困难．将内肋所在区域单独剖分，并对其表面采用增强壁面函数法进行边界层细化．

2 计算结果及分析

笔者采用有限体积法，利用CFD 技术，对27组不同结构参数的内肋管进行流体流动与换热分析．结构参数范围为:螺距10 ～25 mm、肋高0．5 ～1．2 mm、螺旋角70° ～85°，为了便于无量纲分析，文中以下所指的螺距为螺距和管径的比值p/d，肋高为肋高与管径的比值e/d． 雷诺数Re 范围为10 000至25 000，流体特性温度取进出口平均温度．

2．1 螺距对换热及流体流动性能的影响

螺距对内肋管换热性能及流体流动阻力的影响分别如图2、图3 所示．

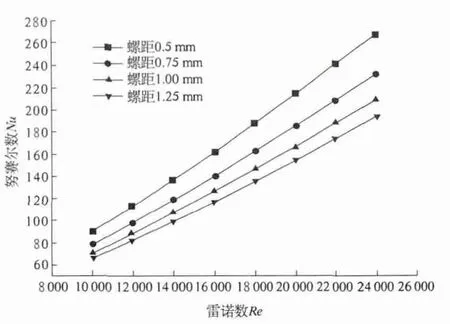
图2 螺距对换热性能的影响Fig．2 Influence on heat transfer of pitch

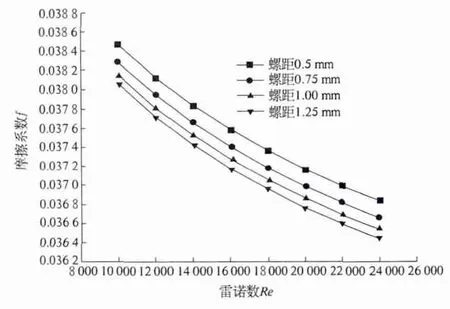
图3 螺距对流体流动阻力的影响Fig．3 Influence on fluid flow of pitch

由图2、图3 可知，随着螺距的减小，内肋管换热性能也随之增强，同时伴随着摩擦系数逐渐增大，努赛尔数Nu 对雷诺数Re 的斜率越来越大，摩擦系数对雷诺数Re 的斜率并无此变化规律，不同螺距时摩擦系数对雷诺数Re 的斜率基本保持一致．这些趋势表明:适当减小螺距可有效提高管侧对流换热能力，同时伴随着阻力降增大，换热性能对雷诺数Re 的增长趋势更为明显，综合性合性能趋势向好．这可归因于，当流体在内肋管内流动时，在近似轴向周期性肋条突起的作用下，迫使管内流体产生周期性的旋转扰流，螺距越小，管内流体旋转流动周期越短，扰动越强烈，为此需付出的代价便是泵功需求增加．在肋条壁面附近，湍动程度增强，如图4 所示，有利于减薄边界层，降低边界层传热热阻，肋条壁面附近热通量增大，如图5 所示．并且，近似轴向的流体旋转运动，减小了主体流速与热流矢量之间的夹角，改善了速度场与热流场的协同程度．

图4 沿Z 轴方向的湍流度Fig．4 Turbulence intensity along Z axis

图5 沿Z 轴方向的热通量Fig．5 Heat flux along Z axis

2．2 肋高对换热及流体流动性能的影响

肋高对内肋管换热性能及流体流动阻力的影响分别如图6、图7 所示．

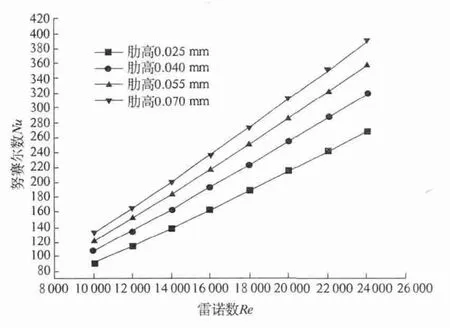
图6 肋高对换热性能的影响Fig．6 Influence oll heat transfer of fin height

由图6 可知，随着肋高的增大，强化管换热性能随之增强，努赛尔数Nu 对雷诺数Re 的斜率也逐渐变大，表明在高雷诺数Re 区域强化管的换热性能随肋高的增加变化得更为明显．由图7 可知，随着肋高的增大，摩擦系数逐渐增大，且摩擦系数增加的比例与肋高增加的比例大致相当． 这些趋势表明:适当增加肋高可有效提高管侧对流换热能力，此时阻力降增加十分明显．这可归因于，当流体在强化管内流动时，在近似轴向周期性肋条突起的作用下，迫使管内流体产生周期性的旋转扰流，如图8 所示．肋高越大，管内流通截面积越小，并且促使扰流的流体体积越大，所需要的泵功越大;肋高越大，迫使扰流越强烈，湍动程度越强．特别是在肋条壁面附近，强化传热更为明显，如图9 所示．

2．3 综合性能及公式拟合

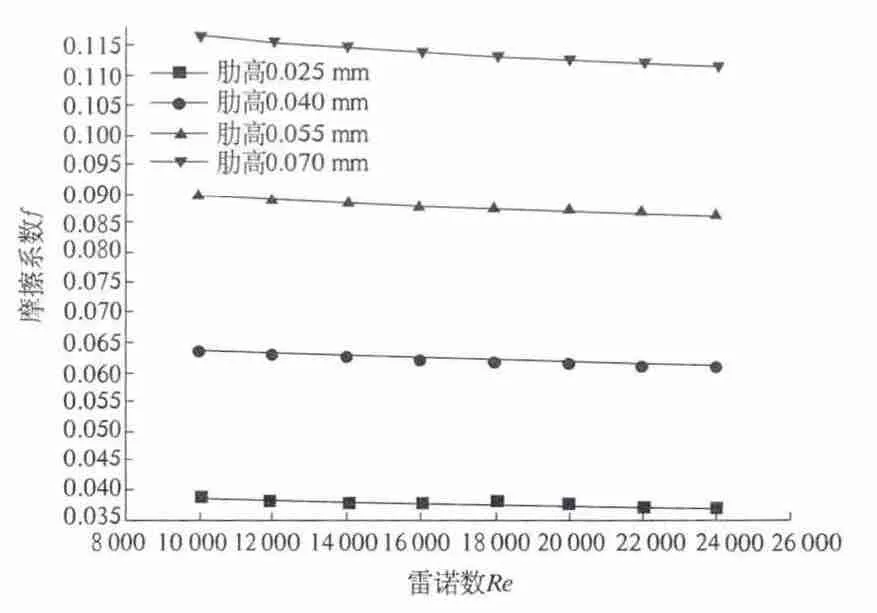
图7 肋高对流体流动阻力的影响Fig．7 Influence on fluid flow of fin height

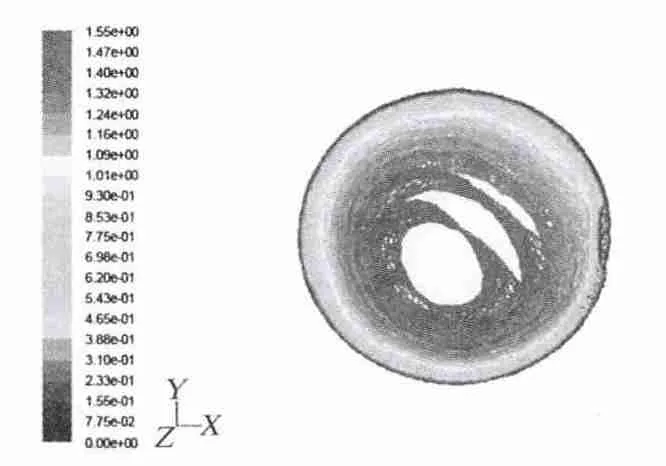
图8 横截面速度场Fig．8 Velocity field of cross section

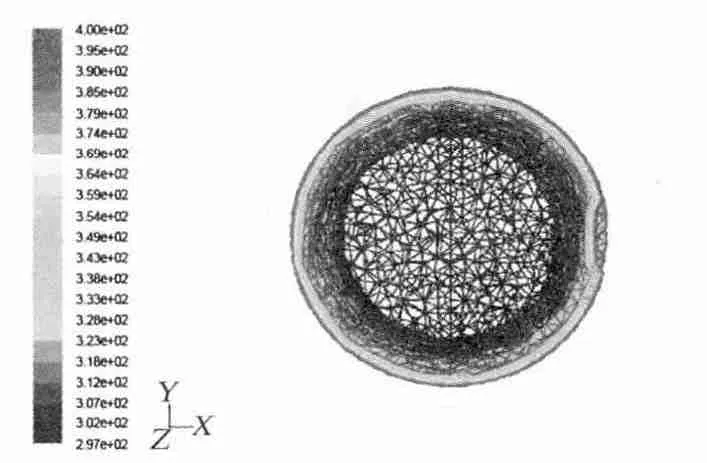
图9 横截面温度场Fig．9 Temperature field of crosssection

利用螺旋内肋管强化传热的同时，管内流体流动阻力增加．几乎所有的强化传热管，其阻力增大的倍数大于强化传热的倍数［7］． 此处采用基于相同泵功率的综合性能评价因子，来表征强化管的综合性能［8］．定义强化因子η 为

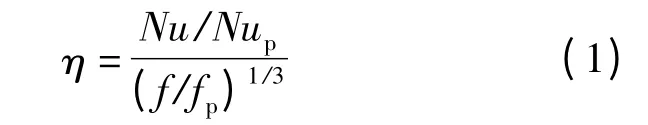
式中:Nu，Nup分别表示强化管及光管的努赛尔数;f，fp分别表示强化管及光管的摩擦系数．依据该强化因子概念，强化因子随雷诺数Re 的变化规律如图10 所示．在雷诺数10 000 至25 000 范围内，强化因子介于1．25 至1．4 之间，表明管内设置螺旋内肋可有效强化换热，是一种行之有效的强化手段．

为了便于工程应用，将所得结果通过多元回归分析得出了包含螺距以及肋高影响因子的换热及阻力特性关联式．换热特性关联式为

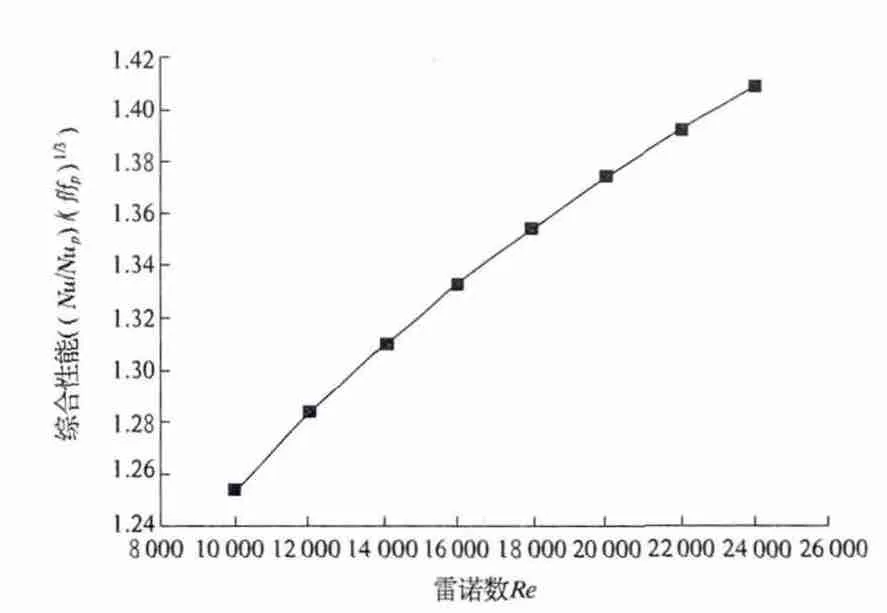
图10 综合性能随雷诺数Re 的变化规律Fig．10 Comprehensive performance variation with Re

Nu=0．001 3×Re0．945×(p/d)-0．358×(e/d)0．364×Pr0．4． (2)

阻力特性关联式为

f=3．202 ×Re-0．05×(p/d)-0．012×(e/d)1．076． (3)

结构参数范围为:对于内径为20 mm 的内肋管，螺距10 ～25 mm、肋高0．5 ～1．2 mm，雷诺数Re 范围为10 000 至25 000．由公式(2)和(3)计算所得的努赛尔数Nu 及摩擦系数f 与数值结果相对误差分别约3．8%和6．5%．

3 结论

(1)适当减小螺距可有效提高管侧对流换热能力，同时伴随着阻力降增大，但是换热性能对雷诺数Re 的增长趋势更为明显，综合性能趋势向好．

(2)随着肋高的增大，强化管换热性能随之增强，在高雷诺数区域强化管的换热性能随肋高的增加变化得更为明显;摩擦系数增加的比例与肋高增加的比例大致相当．

(3)强化管强化因子介于1．25 至1．4 之间，表明设置螺旋内肋是一种行之有效的强化传热手段．

(4)拟合出了换热及阻力特性关联式，可用于相应条件下的换热系数及摩擦系数的计算．

［1］ 王为术，徐维晖，陈听宽，等． 内螺纹管内流动传热特性研究进展［J］． 华北水利水电学院学报，2011，32(4):81 -87．

［2］ CHENG Li-xin，CHEN Ting-kuan． Study of single phase flow heat transfer and friction pressure drop in a spiral internally ribbed tube［J］． Chem Eng Technol，2006，29(5):588 -595．

［3］ JI Wen-tao，ZHANG Ding-cai，HE Ya-ling，et al．Prediction of fully developed turbulent heat transfer of internal helically ribbed tubes -An extension of Gnielinski equation［J］． International Journal of Heat and Mass Transfer，2012，55:1375 -1384．

［4］ GNIELINSKI V，New equations for heat and mass transfer in turbulent pipe and channel flows［J］． Int．Chem． Eng，1976，16:359 -368．

［5］ 刘湘云，史保新，李克天，等． 螺旋内肋管的流阻与换热特性实验研究［J］． 中北大学学报，2010，31(2):108 -112．

［6］ 陶文铨． 数值传热学［M］． 2 版．西安:西安交通大学出版社，2001．

［7］ 顾维藻，神家锐，马重芳，等． 强化传热［M］． 北京:科学出版社，1990:9 -12．

［8］ 张定才，何雅玲，刘启斌，等． 内螺旋肋管流动与传热特性的实验研究［J］． 工程热物理学报，2006，27(6):1029 -1031．