基于激光跟踪测量的火箭橇轨道精测技术分析

何越磊，黎 桂，李再帏

(上海工程技术大学 城市轨道交通学院，上海201620)

0 引言

火箭橇轨道是航空工业重要的大型、高精度地面动态模拟试验设施，其承载火箭橇运行的高速度(600 m/s)［1］，无疑对轨道几何形位的平顺性提出极高的技术要求［2］，即轨道直线性百万分之一的相对精度［3］．现有国内外对高速轨道几何形位静态测量方式主要是以瑞士GRP1000［4］和德国GEDO CE［5］为代表的轨检小车，此种测量方式是通过小车进行逐点移动测量，利用全站仪来确定小车位置，从而提供测量点的轨道几何形位参数［6］．这种基于轨检小车测量方法，为高速铁路轨道精调测量提供了重要的技术支持． 但火箭橇轨道的高低和轨向的偏差精度一般要求在0．2 mm 以下，上述轨检小车的测量精度无疑不能满足这样高精度的要求．因此，需要提出一种能够实现高精度轨道的测量方法，从而为我国高精度轨道几何形位测量提供技术支撑．

笔者采用激光跟踪测量系统对高精度轨道几何形位进行测量;通过球坐标系与轨道空间坐标系进行转换，确定两者之间的对应空间解析几何关系，研究高精度轨道高低和轨向偏差测量方法，进而实现火箭橇轨道几何形位的精确测量．

1 不同空间坐标系间的转换原理

在轨道精调测量工作过程中，为使激光跟踪测量系统球坐标系转换为轨道空间坐标系，必须建立过度空间坐标系进行换算． 采用球坐标系和空间直角坐标系转换原理，将激光跟踪测量系统球坐标系换算为同一坐标原点的控制点空间坐标系，进而基于不同空间直角坐标系的转换原理，将控制点空间坐标系换算为轨道空间坐标系，从而实现激光跟踪测量系统球坐标系与轨道三维空间坐标系的转换．

1．1 球坐标系和空间直角坐标系转换原理

球坐标系是空间极坐标系． 设点Pi(l，α，β)为球坐标系内一点，则点Pi可用3 个有次序数xi，yi，zi来确定．则球坐标系点Pi(l，α，β)与空间直角坐标系点Pi(xi，yi，zi)转换关系如图1 所示．

其中:l 为原点Oi与点Pi的距离，垂直角α为有向线段OiPi与Zi轴正向的夹角;水平角β为从正Zi轴来看自Xi轴按逆时针方向转到有向线段OiMi的角，Mi为点Pi在XiOiYi面上的投影．因此，球坐标系点Pi(l，α，β)可表示为空间直角坐标系点Pi(xi，yi，zi)． 两者转换关系式如式(1)所示．

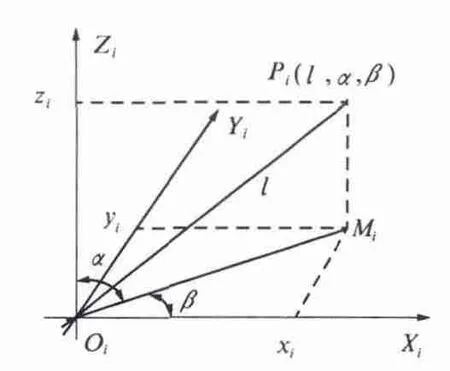
图1 球坐标系和空间直角坐标系转换示意图Fig．1 Spherical coordinate system and spatial Cartesian coordinate system transition diagram

其中:l，α，β 的变化范围分别为:0≤l ＜+∞，0≤α≤2π，0≤β≤π．

1．2 不同空间直角坐标系的换算原理

两个空间直角坐标系间变换需对坐标原点平移参数进行计算，且当坐标轴间互不平行时还要对欧拉角参数，以及坐标系尺度变化参数进行换算［7-9］．不同空间直角坐标系间的坐标变换如图2 所示，对应的布尔莎七参数公式如式(2)所示．

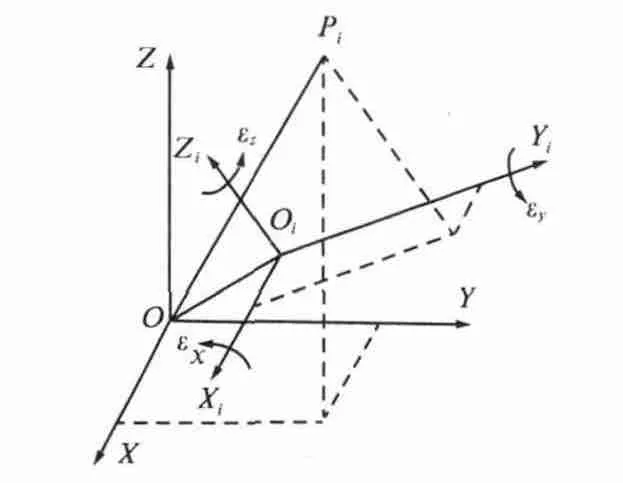
图2 不同空间直角坐标系间坐标变换示意图Fig．2 Schematic coordinates transformation between different spatial Cartesian coordinate system

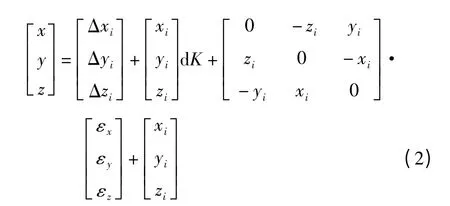
式中:(x，y，z)T和(xi，yi，zi)T分别表示任意点Pi在直角坐标系O-XYZ 及Oi-XiYiZi中的空间直角坐标形式;(Δxi，Δyi，Δzi)T为原点坐标的三个平移参数;dK 为尺度变化系数;εx，εy和εz分别是绕X，Y，Z 轴的三个欧拉角．

2 激光跟踪测量系统球坐标与轨道空间三维坐标的转换算法

2．1 建立相应的坐标系

由于激光跟踪测量系统球坐标系与轨道空间坐标系的坐标原点不在同一点．因此，需要将激光跟踪测量系统球坐标系与轨道空间坐标系间建立一个过度空间坐标系，从而实现测量球坐标系-过度空间坐标系-轨道空间坐标系之间的转换．

这里通过建立控制点空间坐标系来实现上述二次换算．以小里程控制点Cj为原点，控制点Cj与相邻的控制点Cj+1的连线为X 轴，激光跟踪测量系统顶端为Z 轴，根据右手坐标准则确定Y 轴的过度空间直角坐标系;得到的控制点空间坐标系如图3 所示．

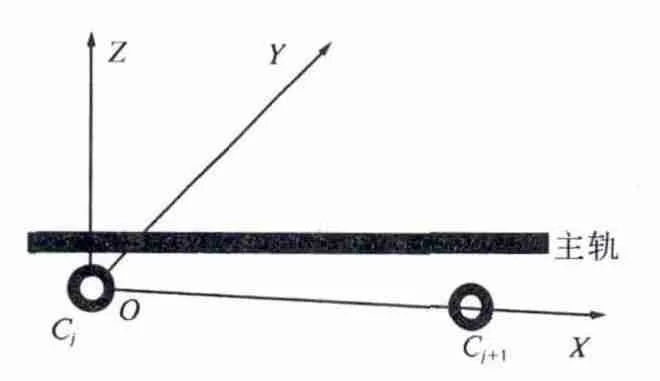
图3 控制点空间坐标系建立示意图Fig．3 Space coordinates of control points established schematic

所建立对应的轨道空间坐标系是以主轨轨头为原点，主轨轨道面内侧为X 轴，垂直于X 轴指向副轨为Y 轴正向，Z 轴为垂直XOZ 面向上组成空间右手坐标系．轨道空间坐标系如图4 所示．

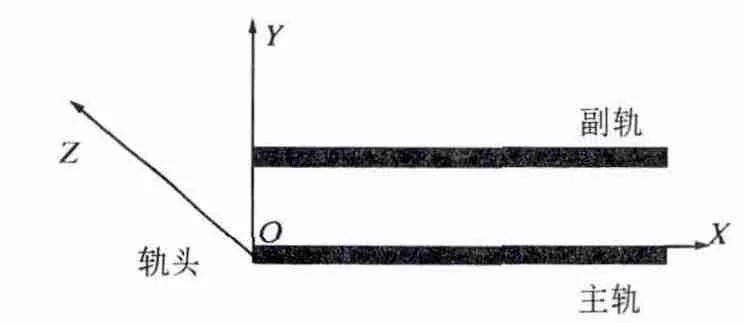
图4 轨道空间坐标系建立示意图Fig．4 Space coordinates of orbital established schematic

2．2 轨道几何形位测量点坐标计算

设点Pj为轨道几何形位的测量点，则采用激光跟踪测量系统对点Pj进行测量，得球坐标系点Pj(r，θ，φ)，其中，r、θ、φ 分别为激光跟踪测量系统测量点的距离、垂直角和水平角．由式(1)可得

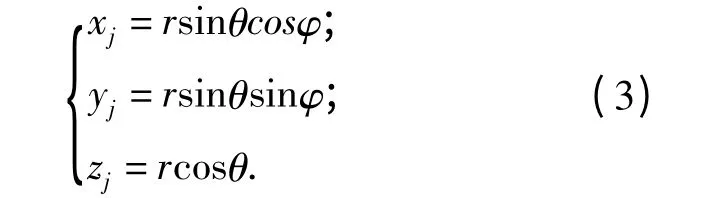
即:轨道几何形位测量点Pj(r，θ，φ)可表示为控制点空间坐标系点Pj(xj，yj，zj)． 将式(3)代入式(2)，可得

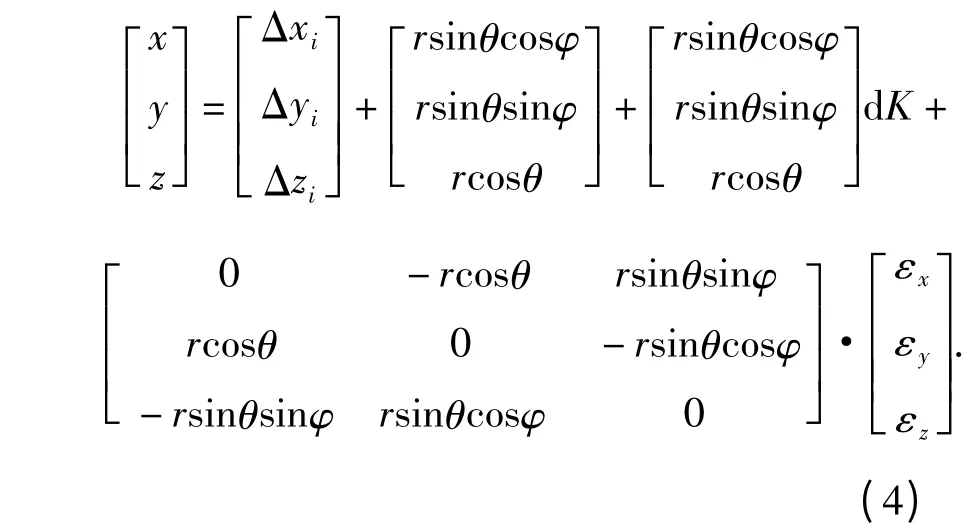
即:球坐标系点Pj(r，θ，φ)可表示为轨道空间坐标系点Pj(x，y，z)．式中，Δxj，Δyj，Δzj分别为测量所得控制点与轨道空间坐标系原点的距离、控制点到轨道中心线的距离和控制点到轨顶的距离．

尺度变化系数dK 由于尺度比变化为零，所以认为等于零．

因控制点空间坐标系和轨道空间坐标系之间只有两个已知共同点，且只需确保控制点空间坐标系Y 轴和Z 轴与轨道空间坐标系完全平行一致，所以绕X 轴的旋转角度εx=0．

绕Y 轴旋转角度εy由于是通过使控制点空间坐标系Z 轴与轨道空间坐标系Z 轴相平行来获取的，因此其计算式为

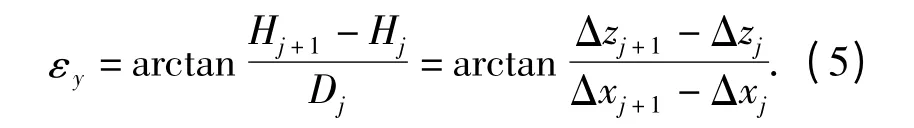
式中:Hj，Hj+1分别表示为第j，j +1 个控制测量点的正常高;Dj为Cj与Cj+1控制测量点间的垂直距离．

绕Z 轴旋转角度εz则是通过使控制点空间坐标系Y 轴与轨道空间坐标系Y 轴相平行来获取的，计算式为

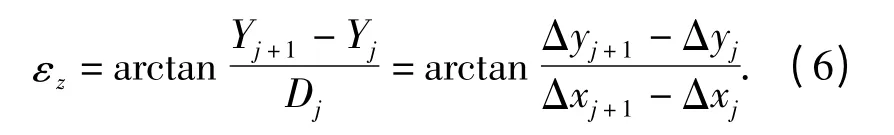
式中:Yj，Yj+1分别表示为第j，j +1 个控制测量点到设计中线的垂直距离．

将已知量Δxj，Δyj，Δzj以及dK =0，εx=0，式(5)、式(6)代入式(4)可得

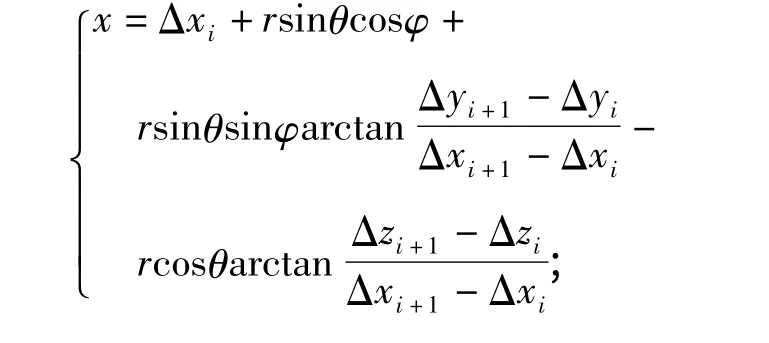
式(7)为激光跟踪测量轨道几何形位测量点的三维坐标计算结果．

3 测量与验证

3．1 测量试验条件

本次试验依据某基地火箭橇轨道的设计参数并对该轨道进行测量;该轨道为9 km 双轨无缝线路，建于长度为15 m 的连续简支梁桥上，各测点的间距为1 m;轨道结构的东侧每隔60 m 设有一个测量控制点，共计151 个控制点．

3．2 激光跟踪测量实际精度评定

为评估笔者采用激光跟踪测量系统测量轨道几何形位坐标的实际精度，采用高精度Leica AT401 激光跟踪仪测量轨道控制网6 个CPⅢ控制点的三维坐标，得到5 组CPⅢ高程坐标差值．将测量得到的5 组CPⅢ高程坐标差值与提供的高程坐标差值进行差异比较，以此来评价激光跟踪测量的实际精度． 按式(8)计算激光跟踪测量控制点高程坐标差差异的均方根误差(RMSE)．

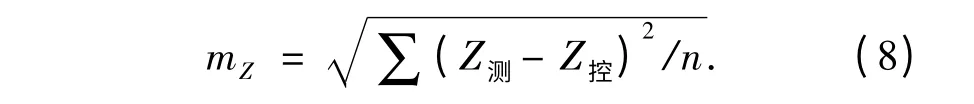
式中:mZ为控制点高程Z 分量的均方根误差;Z测为控制点实测高程坐标差;Z控为控制点提供的高程坐标差;n 为控制点高程坐标差的组数．则得到如表1 所示的精度评定数据．

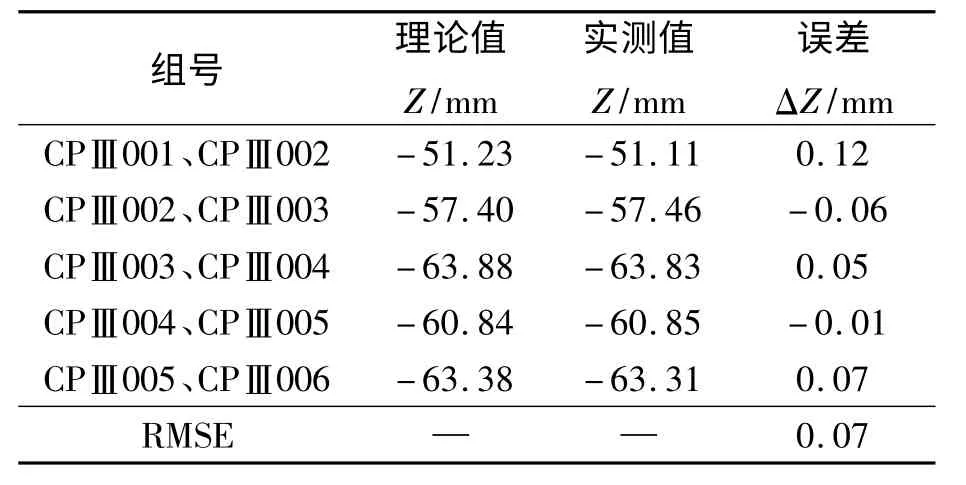
表1 火箭橇轨道控制点高差精度Tab．1 Rocket sled rail control point elevation accuracy

由表1 可知:激光跟踪测量轨道控制点高差精度为0．07 mm，精度较为均匀;激光跟踪测量控制点的实际精度略低于其理论计算精度，主要原因在于CPⅢ轨道控制点起算数据的误差、气象环境变化大影响到仪器本身的精度． 根据火箭橇轨道精调测量对轨道高低和轨向允许偏差小于0．2 mm 的要求，笔者提出的基于激光跟踪测量方法能够满足火箭橇轨道精调测量精度的技术指标．

3．3 火箭橇轨道实测精调数据分析

采用激光跟踪仪对火箭橇轨道几何形位进行测试，这里选取三个样本区段进行分析，其中同样具有15 个测点．则根据已有的控制点参数，利用式(7)对轨道高低和轨向的偏差值进行计算，得到相应的轨道几何形位调整量． 计算结果如表2所示．

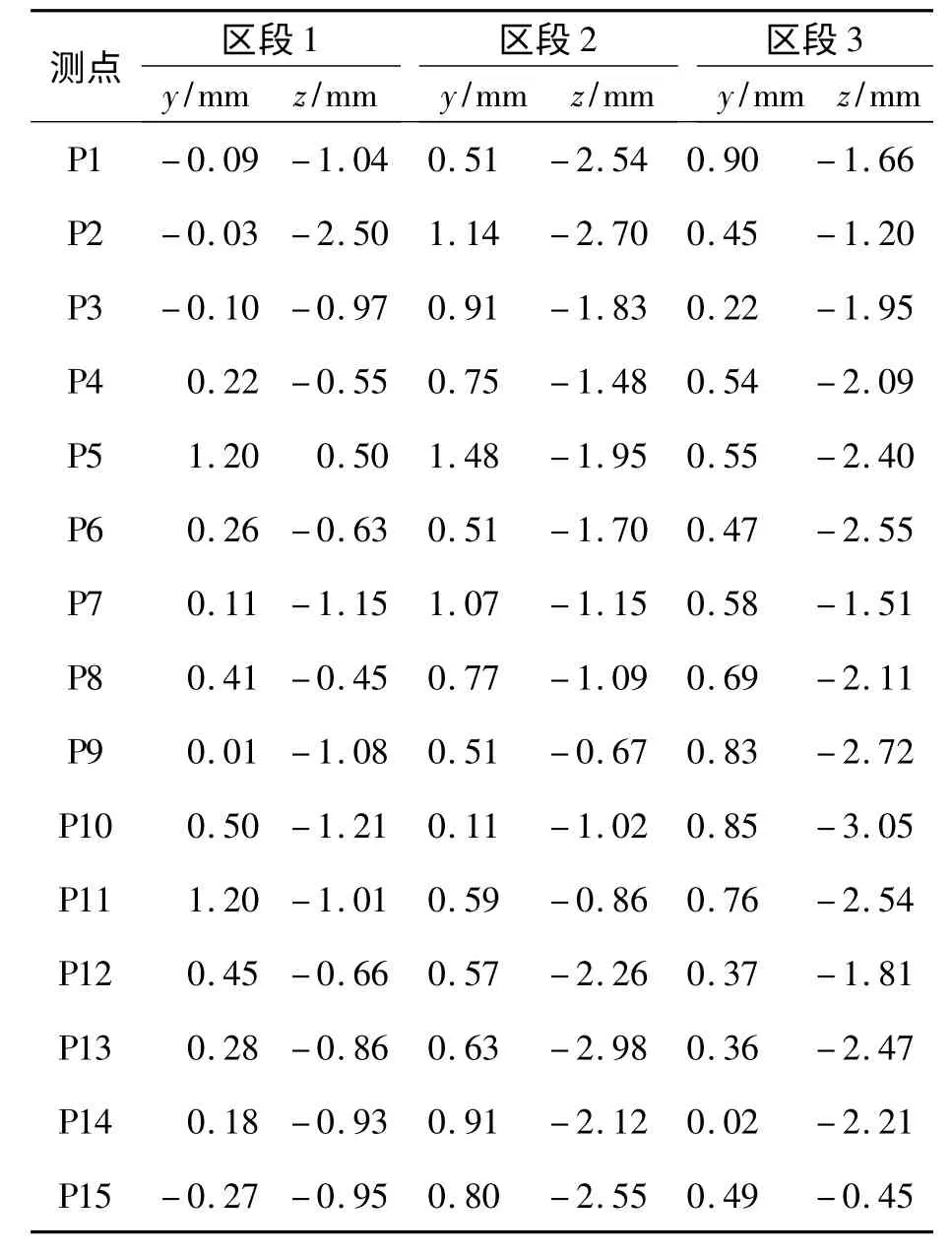
表2 火箭橇轨道高低和轨向精调数据表Tab．2 Rocket sled track fine-tune data

由表2 可知，利用笔者提出的测量方法可有效地计算出火箭橇轨道几何形位的调整量值，且由于所提方法已满足相应的测量精度指标，因此，可以确保所提出的测量方法在实际精调作业中起到良好的作用．

4 结论

笔者采用激光跟踪测量系统对火箭橇轨道几何形位测量的方法，对轨道高低和轨向的三维空间坐标进行计算．主要有以下结论．

(1)从理论上分析了激光跟踪测量轨道高低和轨向的三维坐标计算模型和精度评定方法． 通过实例测量数据及精度评定分析，验证了该方法具有高精度以及可行性．

(2)激光跟踪测量的实际精度略低于其理论计算精度，主要原因在于CPⅢ轨道控制点起算数据的误差、温度和湿度变化大影响到仪器本身的精度．现场测量的环境条件应保持稳定，避免气象环境变化大和振动的干扰对测量精度的影响．

(3)激光跟踪测量轨道高低和轨向的偏差测量精度为0．07 mm，精度较均匀．能够满足火箭橇精调测量的高精度要求，表明该测量方法提高了现有的轨道精调测量的技术水平，可为火箭橇轨道以及高速试验轨道铺设与精调提供高效准确的测量技术．

［1］ 张立乾，邓宗才，时瑾，等．高速滑轨结构参数对橇轨动力响应的影响［J］． 北京工业大学学报，2013，39(2):185 -191．

［2］ 李再帏，练松良． 武广高速铁路轨道不平顺谱特征分析［J］．郑州大学学报:工学版，2013，34(5):52-55．

［3］ 杨兴邦．XB 高精度火箭橇试验滑轨［J］． 中国工程科学，2000，2(10):98 -104．

［4］ 郝亚东，赵杰，樊廷春．基于GRP1000 的无砟轨道精调测量研究［J］．测绘通报，2013(4):52 -55．

［5］ 杨成宽． GEDO CE 轨道检测系统在无砟轨道施工测量中的应用［J］． 铁道工程学报，2009(3):57-61．

［6］ 陈强，刘丽瑶，杨莹辉，等．基于双向近景摄影测量检测轨道平顺度的计算模型［J］． 铁道学报，2012，34(12):83 -89．

［7］ 郭英起，唐彬，张秋江，等．基于空间直角坐标系的高精度坐标转换方法研究［J］． 大地测量与地球动力学，2012，32(3):125 -128．

［8］ 王解先．七参数转换中参数之间的相关性［J］．大地测量与地球动力学，2007，27(2):43 -46．

［9］ 欧朝敏，黄梦龙．地方坐标到2000 国家大地坐标转换方法研究［J］．测绘通报，2010(9):26 -28．