基于测试结果调整语句出错概率方法＊

王蓁蓁

（1.金陵科技学院信息技术学院，江苏南京211169；2.江苏省信息分析工程实验室，江苏南京211169）

1 引言

运用从软件测试中获得的信息自动确定错误位置是很重要的一种技术手段，有关方法可以统称为TBFL（Testing－Based Fault Localization）方法［1～12］。

文献［3］讨论了六种涉及动态定位的TBFL方法：Dicing方法（Agrawl et al，1995）、TARANTULA方法（Jones et al，2002；Jones and Harrold 2005）、Nearest Neighbor Queries方法（Renieris and Reiss 2003）、CT（Cleve and Zeller 2005）、So－BER（Liu et al，2005）和Liblit05（liblit et al，2005），发现它们都忽略了实施相似性的测试用例可能产生的问题。同样，文献［6］也指出，相似性的测试用例可能会损害TBFL方法的功效。为了解决该问题，文献［3］主要是运用模糊集合理论提出了SAFL（Similarity－Aware Fault Localization）方法。在测试实践中，测试用例的相似性总是难以避免的，所以讨论类似SAFL方法和寻找更有成效的错误定位方法是有价值的。

然而测试实践里也存在这样的问题，就是没有充分利用原程序和测试用例本身所包含的信息去辅助测试结果寻找错误根源，这不仅是一种“资源浪费”，而且有时对程序中隐蔽错误的揭露“无能为力”，这特别表现在，当测试用例全部通过时，测试对程序中没有被揭露出的错误就“无话可说”。为了解决这个问题，文献［12］提出了一种新的基于随机理论的TBFL方法，该方法对减少相似用例的伤害性方面也有成效。

文献［12］认为软件虽然是由高度负责和有丰富专业知识的程序员编写的，但是由于软件的复杂性和“非物质性”，一些“偶然”因素所导致的错误是无法避免的，所以将整个待测程序看成是一个随机变量，把程序员或测试员在测试前关于程序中每个语句（或各个构件）出错的可能性的估计抽象为该随机变量的先验分布。同样，就测试用例捕捉程序的错误能力而言，也视测试用例集为另一个随机变量，其分布就是它们的捕捉错误的能力的抽象表示。在这些信息的基础上，综合利用每个测试用例的测试结果类型（失败或通过）和它们覆盖语句的情况，对程序里每个语句的（先验）概率作“综合性”调整，调整后的概率称为后验概率，最后根据这个后验概率对错误语句进行排序，为程序员寻找错误提供导向。

随机TBFL算法可以用如图1所示的流程图（参见文献［12］的图3）表示（稍加改变）。

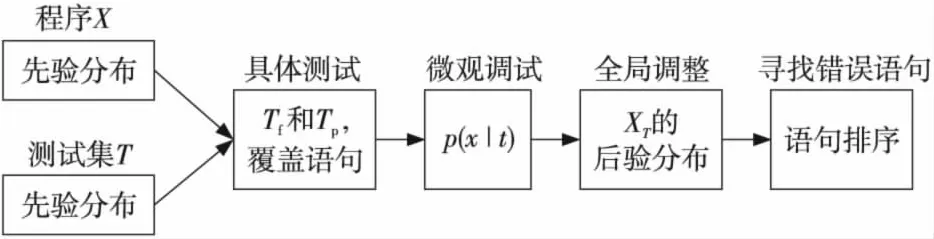
Figure 1 Flowchart of random TBFL algorithm图1 随机TBFL算法流程图

图1很好地阐述了文献［12］提出的随机TBFL算法的精神。算法细节请参见该文献。文献［12］指出，X的先验分布是根据程序“样式”分析得到的，测试集的（先验）分布与设计测试用例的类型、意图有关，它们分别与程序里语句的真实错误和测试用例具体实施结果无关，并且这些先验知识即使粗糙，只要大体上“正确”，当它们和测试实践产生的结果从微观和宏观两个层次上进行关联以后，就会对语句的错误定位有较大帮助。文献［12］在一些具体实例上，把它和前述几个方法进行对比，证实了这一点。

本文遵循文献［12］的思路，但对其算法作了改进。主要思想是：首先把程序X的先验分布从测试活动里“分离”出来，因为程序的先验分布的不精确可能会影响“单纯的”测试活动的结果，这种分离也符合当前流行的软件测试的主流方向。其次，测试集T的先验分布也从具体测试里分离出来，等到估计测试结果的影响时才加入考虑。其具体思想可用图2表示。

本文的算法称为基于测试结果的随机TBFL方法，为了叙述简洁，下文简称它为新方法。

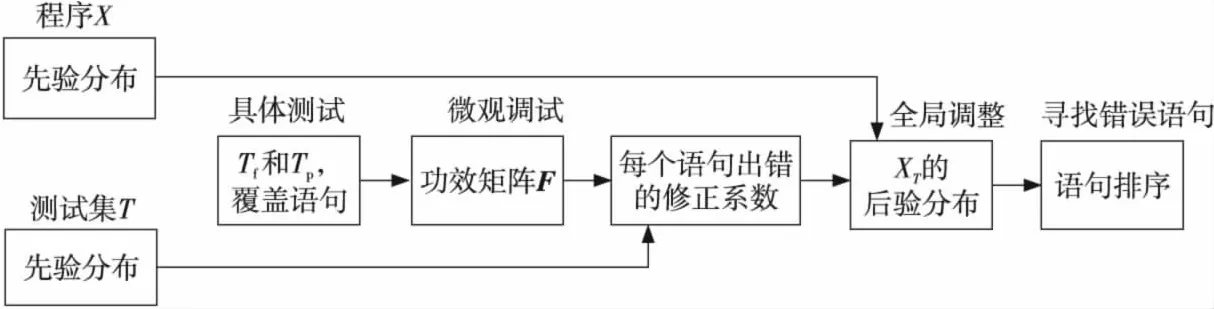
Figure 2 Flowchart of random TBFL algorithm based on testing results图2 基于测试结果的随机TBFL方法流程图

本文的其余部分组织如下：第2节给出新算法大致框架；第3节给出TBFL算法评价标准；第4节为实例分析；第5节为结论和展望。

2 基于测试结果随机TBFL算法模型

2.1 程序随机变量X

用X＝｛x1，x2，…，xm｝＝｛xi｜xi是程序语句，1≤i≤m｝表示程序，它是语句的集合，其中语句xi的下标i可按程序的书写方式编码。假定程序是“精心”编码的，即是由有责任心且有熟练技能的开发人员编写的。然而由于各种各样不可控制的因素的影响，程序发生错误仍然是难免的。把程序的错误归咎到语句层次上，认为它的每个语句出错是一种偶然现象。因此，视程序X为（出错）随机变量，用rk＝P（xk出错）表示语句xk出错的概率。rk（k＝1，2，…，m）是程序X随机变量的先验概率质量函数。可以根据开发人员的经验、历史资料分析各种语句类型通常犯错误的可能性，也就是根据程序X的“样式”确定rk之值。当然不同的人可能有不同的估计值，然而即使这些估计值粗糙、不精确，只要大体上反映了程序编写时的客观情况，它们对于语句错误定位算法都是有用的。如果缺少这方面的资料，可以按照统计学上“同等无知”原则，令rk＝1/m，k＝1，2，…，m，其中m是程序X的语句总数。

2.2 测试随机变量T

用T＝｛t1，t2，…，tn｝表示测试用例集，其中tj（j＝1，2，…，n）表示测试用例，以下有时简称为用例。它们是用来对程序X进行测试的。设计测试用例的目的是想捕获程序错误，它们捕获错误的可能性也是随机现象，可以根据测试人员的经验和软件测试理论确定每个用例捕获错误的概率，用pi＝P（ti发现错误）表示ti用例能检测出错误的概率。若没有这方面的资料，在算法里不妨假设pi＝1/n，其中n是T中测试用例的总数，这也是统计学中“同等无知”原则的应用。

2.3 具体测试

用T测试X后，可以将T中用例分为两类：Tp和Tf。Tp表示测试程序时没有发现错误的所有用例组成的子集合，Tf表示测试程序时发现错误的所有测试用例组成的子集合。Tp和Tf中的用例分别称为通过用例和失败用例。每个用例覆盖语句的具体信息也可从测试活动里提取出来。一般来说，从具体测试活动中可以得到上述两类信息。

2.4 测试功效矩阵F

根据具体测试结果，构造测试用例集T的功效矩阵F。F是一个n×m阶矩阵，列对应程序X

的语句，行对应测试集T里的用例。即第i行为：ti＝ti1ti2ti3ti4…tim，i＝1，2，…，n

其中，tij（j＝1，2，…，m）表示第i个用例测试结果对语句xj出错概率“纯粹功效”。我们建议：

其中，i＝1，2，…，n；j＝1，2，…，m；c1、c2都是大于1的正数。

设计tij的思想是，如果ti是失败用例，则它覆盖语句应承担较多责任。用α表示ti覆盖的语句可能犯错误的概率，β表示ti未覆盖的语句出错的概率，令α＝c1β，c1＞1是合理的。于是，由αl＋β（m－l）＝1，α＝c1β，可得：

若ti是通过用例，则它未覆盖的语句对程序出错应承担较多责任。同样，用α表示ti覆盖的语句可能犯错误的概率，β表示ti未覆盖的语句出错的概率，这时令β＝c2α，c2＞1是合理的。于是，由αl＋β（m－l）＝1，α＝c2β，可得：

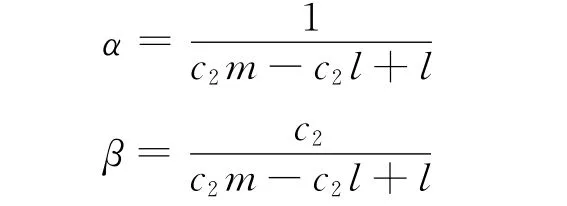
为了计算简单起见，下面算法皆采用c1＝c2＝2。即：

其中，i＝1，2，…，n；j＝1，2，…，m。

以公式（2）产生的tij（i＝1，2，…，n；j＝1，2，…，m）为元素的矩阵称为（测试集）功效矩阵，记为：

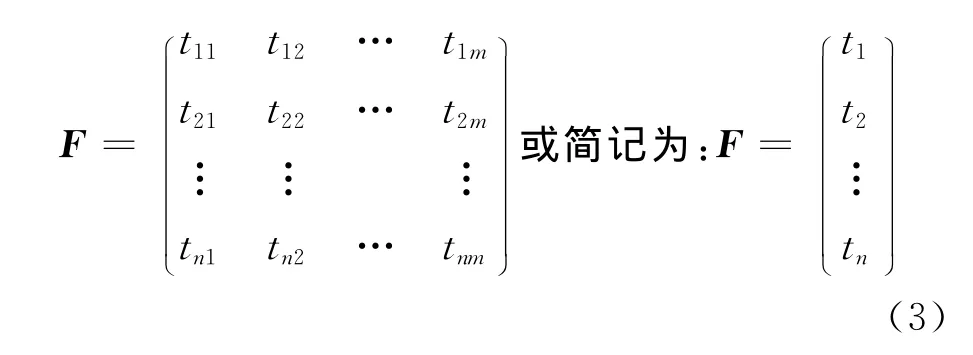
2.5 修正系数

计算向量b＝（b1b2…bm），其中bi表示对程序X第i个语句xi出错概率进行调整的修正系数，其定义如下：

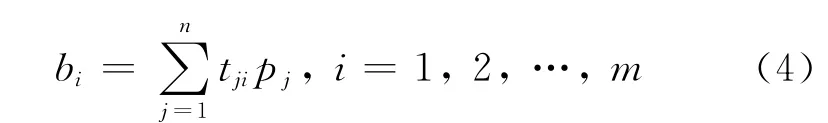
固定xi，我们知道tji是从用例tj的观点看待语句xi出错的可能性，而pj是用例tj捕获错误的能力，因此对于语句xi而言，把t1i，t2i，…，tni按照p1，p2，…，pn加权求和得到xi出错的修正系数是合理的。

今后称向量b为修正向量，其中i＝1，2，…，m，元素bi称为xi的修正系数。

2.6 后验概率

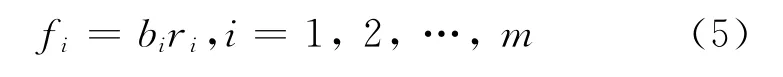
用向量f＝（f1f2…fm）表示（准）随机分布，其中fi定义如下：称向量f为原程序X的（准）后验概率分布。也可以将f“标准化”，即令a＝f1＋f2＋…＋fm，则由fi←fi/a得到的序列是“真正”概率分布，记如此分布的随机变量为XT。

然而就对语句出错的排序而言，未标准化的f和标准化后的f作用是一样的，今后我们就用未标准化的f作为XT的（准）概率分布，并省略“准”字，它与标准化后的概率不难从上下文中分辨出来。

2.7 语句出错排序

根据fi（i＝1，2，…，m）的值，从大到小排序，如果有若干个值相等，则按它们相应的语句出现的次序排序（语句编号较小的排列在前），得到：

把式（6）中具有相等值的fij归为一类，然后把fij换成对应的语句xij，这样就把程序语句按出错可能性从大到小排列成若干个等级。假如是k个等级，则写成表格形式，如表1所示。

Table 1 Rank of faulty statements表1 出错语句排列等级

程序员可以按照上面次序寻找出错语句，一般地，找到真实错误以后，就重新用测试集T测试，若仍有失败用例，再按表1（或者式（6））寻找下一个错误语句，……，如此进行下去，直到用例全部通过为止。当然中途也可以更改测试用例（增添或修改）。

3 TBFL算法评价标准

假如某个TBFL算法已把程序语句出错可能性排列成类似于表1的等级，它也可看作是语句出错可能性的排序式（6）。设程序X真实错误语句为xi，xi，…，xi，定义三个评价标准：12s

D1＝真实错误语句出现在表1中的等级之和，

D2＝真实错误语句出现在表1中的次序（即xi1次序为1，…，xim次序为m）之和，

若有两个TBFL算法，可以分别计算它们相应的D1、D2、D3之值，一般地，D1与D2越小越好，D3越大越好，D1、D2之值越小越好是明显的，而D3越大表示该TBFL算法辨别能力较强，区分语句的精度较高，所以相应的算法就比较优越。

4 实例分析

为了和Dicing方法、TARANTULA方法、SAFL方法以及文献［12］提出的方法（下面简称Wang方法）作比较，我们采用的实例和文献［12］中的实例一致。

本文主要用文献［12］中图1（该图来源于文献［3］）里给出的程序和测试用例。为了阅读方便，把它复制于下，在本文中标记为图3。

在下面的讨论中，称图3中的程序为程序I，该程序的错误语句是x2（x2应为：m＝z）和x7（x7应为：m＝x）。

把程序I中的错误语句x2：“m＝x”改为正确语句x2：“m＝z”，其余语句保留不变，称这个变体为程序II。程序II中有一个错误语句x7（m＝y）。

Figure 3 A faulty program and relative test cases图3 错误程序和相关测试用例集信息

将程序I的x2（m＝x）改为x2（m＝z），x11（else if（x＞z））改为x11（else if（x＜z）），其余语句不变，称这样的变体为程序III。

将程序I的错误语句x7（m＝y）改为正确语句x7（m＝x），其余语句不变，称这个变体为程序IV。

显然上述四个程序的真实错误语句不尽相同，但它们“样式”完全相同，所以估计每个语句出错的（先验）可能性是一样的，它们都是“客观”存在的。现在不管是哪个程序，我们都用X＝｛x1，x2，…，x13｝这个程序变量表示它，并且它的先验分布为：

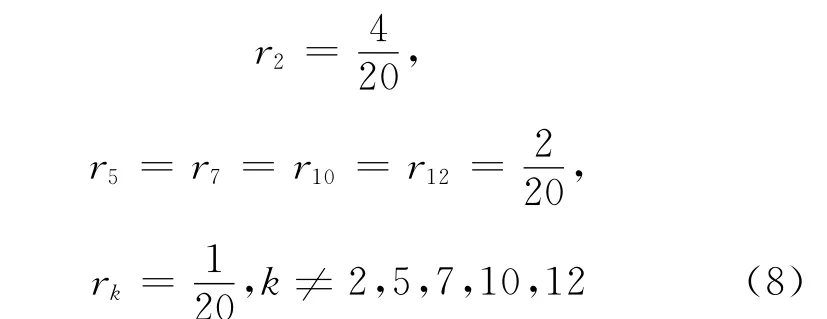
这个先验分布是文献［12］中采用的，关于它的详情，请参看该文献。在理论上，上述四个程序语句出错情况是这个随机变量X的四个“具体实现”。

在下面的讨论中，称图3中的全部八个用例（即Test suite1＋Test suite2）组成的测试集为T，其中前四个用例（即Test suite1）组成的测试集为T＊。沿用文献［12］中的术语，T为冗余测试集，T＊为无冗余测试集。粗略地说，在文献［12］中，术语冗余指用例覆盖的语句至少几乎是完全相同的。详情请见文献［12］。

测试随机变量T的先验分布为：

测试随机变量T＊的先验分布为：

这些分布都是文献［12］采用的，详情也请参看文献［12］。

例1 用T、T＊两测试集测试程序I。

用T测试集测试程序I，结果是：Tp＝｛t3，t4，t5，t6，t7，t8｝，Tf＝｛t1，t2｝，其覆盖语句情况可从图3中看出。

利用公式（2）计算功效矩阵F中的诸元素tij，i＝1，2，…，n；j＝1，2，…，m。由它们组成的测试功效矩阵F如下（为了清楚起见，列用语句xi标出，中间的虚线是为了区分Test suite1和Test suite2画的）：

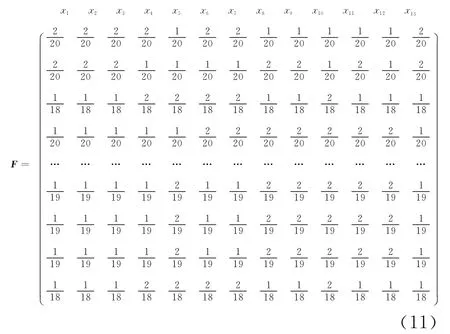
由F矩阵和T的分布（式（9）），利用公式（4）计算修正系数如下：

如果令P＝（p1p2…pn）为T测试集概率分布向量，则修正系数向量b＝（b1b2…bm）可以由下面矩阵乘法得出：

由式（12）计算出的修正系数向量和X的先验分布（式（8）），利用公式（5）即fi＝biri（i＝1，2，…，m），可以求出程序X的（未标准化的）后验概率如下（其中因子N＝1/220）：

最后，根据fi的值，按从大到小排序，并根据表1划分成等级排列如表2第二行（上面标号为等级标号）。

Table 2 Rank of statements of program I under test suite T and under test suite T＊表2 程序I分别在测试集T和在测试集T＊下的出错语句排序

用测试集T＊测试程序I，T＊测试结果即为前面的Test suite1的测试结果。因此T＊测试功效矩阵F＊即由公式（11）中前四行（虚线以上部分）组成。设T＊的先验分布向量为P＊，由式（10）得到，于是由T＊测试得到的修正系数向量b＊，可由式（12）即b＊＝P＊·F＊计算，再由b＊和X的先验分布（式（8）），利用公式（5）得到程序X的（未标准化的）后验概率如下（具体计算步骤省略）：

按照上面的值，把语句出错可能性从大到小排成等级，见表2第三行。

现将本文算法（下面简称为新算法）与文献［12］中的算法（记为Wang方法）以及Dicing方法、TARANTULA方法、SAFL方法进行比较，除了本文算法以外，其余算法的资料都摘自于文献［12］。

关于可能出错语句的（等级）排序：

分析式（13）中数据，正如文献［12］指出，无论测试集是否冗余，Wang方法除了在T测试时，把正确语句x10排在错误语句x7前，与T＊测试时“正确排序”有些差异以外，就这个具体例子而言，Wang方法比前几种方法都优。同样，从式（13）中也可看出，本文算法和Wang方法的排序在T下几乎一样，在T＊下是完全一致。现在我们在T测试下，用式（7）给出的标准比较一下这两个算法（回忆x2、x7有错）：

Wang：D1＝1＋3＝4，D2＝1＋3＝4，D3＝7；

新算法：D1＝1＋3＝4，D2＝1＋3＝4，D3＝9。

虽然它们的D1和D2都相同，但是本文的算法比Wang方法精细，所以本文算法较优。

例2 用T＊测试集测试程序II

程序变量X和测试集T＊变量的先验分布同前，分别由式（8）、式（10）表示。用测试集T＊测试程序II时，每个用例覆盖语句的情况和前例中一样，没有变化，但t2在前例中是失败用例，在本例中是通过用例，其他用例的结果类型未变，即在本例中Tf＝｛t1｝，Tp＝｛t2，t3，t4｝。

利用测试资料，可以构造T＊测试功效矩阵，然后算出修正系数，从而得到X的后验分布（中间过程省略）fi值，由fi值可把程序语句依出错可能性从大到小排成等级，并与Wang方法对比，如表3所示。

Table 3 Rank of program II’s statements under test suite T＊and comparison with Wang approach表3 程序II在测试集T＊下语句排序及和Wang方法对比

由于排序完全一样，所以它们的功能在这个具体例子中是一样的。

例3 用测试集T＊测试程序III

程序变量X和测试集变量T＊的分布同前，分别由式（8）、式（10）表示。用T＊测试程序III，结果类型为：Tf＝｛t1，t2，t3｝，Tp＝｛t4｝。至于覆盖语句方面，t1、t4覆盖的语句和它们在例1中覆盖的语句情况一样，t2、t3覆盖语句情况有所变动，t2覆盖x1x2x3x8x9x11x12x13；t3覆盖x1x2x3x8x9x11x13，因此测试集T＊的功效矩阵需要重新计算。具体计算省略，同样修改系数和后验概率的计算过程也省略，按照后验概率的值，把程序III中的语句按出错可能性大小排成等级并与Wang方法比较，如表4所示。

Table 4 Rank of program III’s statements under test suite T＊and comparison with Wang approach表4 程序III在测试集T＊下语句排序及和Wang方法对比

根据文献［12］的分析，程序III有严重的逻辑错误，它是由于语句x11的错误选择导致的，具体表现在x2语句的设置上，即程序流程中有的路径要求语句x2为“m＝z”，有的路径要求语句x2为“m＝x”。因此，程序III的错误语句可以归结为x2、x7、x11、x12。详细分析请见文献［12］。

现在评价在这个具有隐蔽逻辑错误的程序上两个算法的功效：

因为x2是个“设置语句”，要求程序员有较高的编程技巧，但是一旦检查出x2语句在设置上的“逻辑”困境，就可以发现是语句x11的设计问题以及连带产生的语句x12的错误，所以实质上是要考察x2、x7。然而就这种考察而言两个算法的功效几乎一致，如果就x2、x7、x12的考察而言（因为考察了这3个语句，肯定就会发现x11有错），则两个算法在它们的“线性”次序上完全一致。

例4 用例全部通过的测试

仍然考虑程序I，它有两个错误语句x2、x7，程序变量X的先验分布由式（8）表示。

现在用测试集To＝｛o1，o2，o3，o4｝对程序I进行测试，其中用例的设计为：o1＝｛10，13，15｝，o2＝｛8，6，4｝，o3＝｛5，9，2｝，o4＝｛17，19，2｝。To的先验分布为均匀分布，即P1＝P2＝P3＝P4＝1/4，也就是说每个用例捕获错误的可能性相同。

用To测试发现它们都是通过用例。它们覆盖语句情况是：o1覆盖6个语句（x1，x2，x3，x4，x5，x13）；o2覆盖7个语句（x1，x2，x3，x8，x9，x10，x13）；o3覆盖8个语句（x1，x2，x3，x8，x9，x11，x12，x13），o4覆盖情况和o1相同。

利用上述数据可以计算To测试功效矩阵、修正系数和后验概率，具体计算省略，根据后验概率把语句排序结果与Wang方法的结果并列如表5。

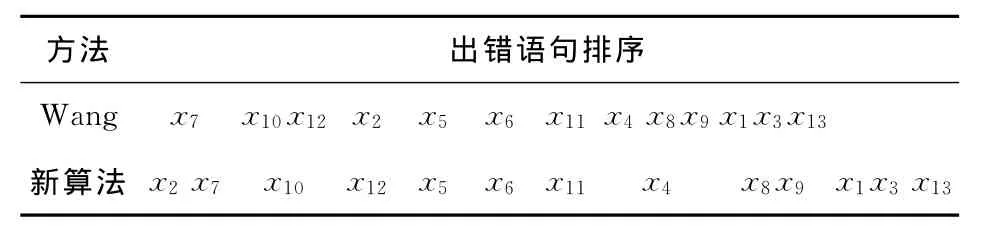
Table 5 Rank of program I’s statements when test cases are passed and comparison with Wang approach表5 程序I在测试用例全部通过情况下出错语句排序及和Wang方法比较

显然，无论采用哪个标准（D1、D2还是D3），本文算法都比Wang方法好！一般来说，测试员只能报告软件缺陷存在，却不能报告软件缺陷不存在。通常的测试在所有用例都通过时，对于软件缺陷都“无话可说”。因此，文献［12］的算法和本文的算法在这种情况下更有价值，特别是在这个例子里，本文算法竟然把x2x7排在最前面，更使人相信新算法的优越性。

例5 先验概率未知情况

取程序I，但程序变量X的先验分布未知，这时令X服从均匀分布，即rk＝1/13，k＝1，2，…，13。取测试集T＊，但测试集变量T＊的先验概率未知，这时令T＊服从均匀分布，即pj＝1/4，j＝1，2，3，4。用测试集T＊测试程序I，结果与例1中的测试结果完全相同。所以，这里测试集T＊的功效矩阵与例1中用T＊测试的功效矩阵相同。但修改系数，进而后验概率的数值不同，计算方法同前，省略。

兹将Wang方法和本文算法在这个例子中关于语句出错可能性从大到小排序，如表6所示。

Table 6 Rank of statements under unkonwn prior probability and comparison with Wang approach表6 先验概率未知情况下出错语句排序及与Wang方法比较

这两个算法功效基本上相同，但是都不怎么好。正如文献［12］指出，随机算法的精神是挖掘程序中和测试集中包含的固有信息，并把它们掺合进具体测试实施中，才能发挥更大的功效。本文算法和文献［12］算法都是随机算法，只是利用先验知识这个丰富“资源“的方法不同罢了。所以，当这些先验知识缺乏时，功效降低甚至丧失，也就不难理解了。然而把这里的结果和式（13）比较就可以发现，在“最坏”（即没有挖掘出程序和测试集里的信息）的情况下，本文算法也和上述三个方法相当，而且仅就错误语句x2来说，本文算法重视程度较逊于TARANTULA方法，但比Dicing方法、SAFL方法的重视程度高。

例6 测试用例设计较好的情况

在前面的实例中，对程序I等的测试所用的测试集，无论是T、T＊还是To都设计得不好。现在根据软件测试经验，应该设计用例集，使得它们执行时能覆盖程序I（等程序）的每一条路径。为此引入新的测试集：

其中，e1＝｛6，7，9｝，即输入x＝6，y＝7，z＝9，e2＝｛8，7，9｝，e3＝｛10，7，9｝，e4＝｛11，10，7｝，e5＝｛9，10，7｝，e6＝｛8，10，9｝。因为程序I和它的变体都是求三个输入整数中的中位数，而三个数按“小、中、大”不同方式排列共有六种排列，所以如上设计的测试用例集可以通过程序I等程序的每条路径，它是比较好的用例设计。当然，对于现在讨论的程序来说，设计好的测试集至少还应该包括输入的三个数中有若干个相等的用例，以及比较大的整数用例，关于后者并不是本质问题，至于前者，由于前面的测试集T、T＊都包含了这种用例。我们已经看到算法对这些用例的适应程度，所以为了说明问题，设计了T′。

下面用T′测试程序I、程序II和程序IV，无论用T′测试哪个程序，根据设计它的意图来看，每个用例捕获错误的可能性相同，即pi＝P（ei）＝1/6，i＝1，2，…，6。注意T′的均匀分布是“客观”的先验分布，并不是由于“同等无知”得到的。

由于算法与上面一样，因此计算过程省略不写。只把在T′测试下，新算法和文献［12］中算法对语句排序的结果对比列出，如表7～表9所示。

Table 7 Rank of program I’s statements under test suite T′and comparison with Wang approach表7 用T′测试程序I语句可能出错排序及和Wang方法比较

两个算法排序完全一致，且把有错语句x2、x7排在前两位，但新算法D3＝9比Wang方法D3＝7大，所以更精细。

Table 8 Rank of program II’s statements under test suite T′and comparison with Wang approach表8 用T′测试程序II语句可能出错排序及和Wang方法比较

除了排在前两位的x2、x7的次序不同外，其他次序完全一样，就错误语句x7的排列而言，Wang方法好，就排列的精细而言，新算法为好。

Table 9 Rank of program IV’s statements under test suite T′and comparison with Wang approach表9用T′测试程序IV语句可能出错排序及和Wang方法比较

两个算法的排序完全一致且把错误语句x2排在第一位，但是新算法显然比Wang方法精细。

5 结束语

就我们所知，文献［12］为TBFL方法引入了一个新类型，其精神是用随机理论考察软件测试问题。本文对文献［12］中的算法做了一点改进。正如引言里所说，主要是把程序X的先验分布和测试集T的先验分布从测试活动中分离出来，这种分离是有好处的。因为测试活动和它的结果都是“客观”的，它是这种类型算法中的科学成分，而程序变量X和测试集变量T的先验分布是“主观”的，它是这种类型算法里的艺术成份。文献［13］认为，在最严格的数学学科里，数学思维也包含这两种成份。另外，文献［14］用朴素模糊逻辑阐述了许多中医问题，说明了定性推理的重要性以及它和逻辑（或说是定量）推理的关系。可以认为X和T的先验分布这个艺术部分属于定性推理，这一点可以从它们分别是从分析程序“样式”和设计用例的“意图”得到的看出。现在我们的算法把文献［12］算法中包含的科学（逻辑）成份和艺术（定性）成份分离，就可以让测试结果交给不同的人处理，不同的人可以根据他们的经验对这些客观资料作创造性处理。如果若干个测试员或程序员平行处理这些测试结果，就可能会得到不同的排序情况，综合他们的结论，对修正较大较重要的软件缺陷是有益的。这和许多医学专家会诊一个疑难病症，对医疗是有帮助的一样。

本文提出的算法只是对文献［12］引入的随机TBFL方法的一种改进，今后，我们将努力开发新的随机TBFL方法，并将其应用到实际的测试活动中去。

致谢：衷心感谢徐宝文教授、邢汉承教授、周毓明教授对本文工作的支持。审稿人对本文提出了有价值的修改意见，在此表示衷心感谢！

［1］ Agrawal H，Horgan J，London S，et al.Fault localization using execution slices and dataflow tests［C］∥Proc of the 6th International Symposium on Software Reliability Engineering，1995：143－151.

［2］ Cleve H，Zeller A.Locating causes of program failures［C］∥Proc of the 27th International Conference on Software Engineering，2005：342－351.

［3］ Hao D，Zhang L，Pan Y，et al.On similarity－awareness in testing－based fault localization［J］.Automated Software Engineering，2008，15（2）：207－249.

［4］ Kyriazis A，Mathioudakis K.Enhance of fault localization using probabilistic fusion with gas path analysis algorithms［J］.Journal of Engineering for Gas Turbines and Power，2009，131（5）：51601－51609.

［5］ Jones J A，Harrold M J，Stasko J.Visualization of test information to assist fault localization［C］∥Proc of the 24th International Conference on Software Engineering，2002：467－477.

［6］ Jones J A，Harrold M J.Empirical evaluation of the tarantula automatic fault－localization technique［C］∥Proc of the 20th IEEE/ACM International Conference on Automated Software Engineering，2005：273－282.

［7］ Liblit B，Naik M，Zheng A X，et al.Scalable statistical bug isolation［C］∥Proc of the ACM SIGPLAN Conference on Programming Language Design and Implementation（PLDI），2005：15－16.

［8］ Schach S R.Object－oriented classical software engineering［M］.Beijing：China Machine Press，2007.

［9］ Liu C，Yan X，Fei L，et al.SOBER：Statistical model－based bug localization［C］∥Proc of the 13th ACM SIGSOFT Symposium on Foundations of Software Engineering，2005：286－295.

［10］ Renieris M，Reiss S P.Fault localization with nearest neighbor queries［C］∥Proc of the 18th International Conference on Automated Software Engineering，2003：30－39.

［11］ Zeller A.Isolating cause－effect chains from computer programs［C］∥Proc of the 10th ACM SIGFOFT Symposium on Foundations of Software Engineering，2002：1－10.

［12］ Wang Zhen－zhen，Xu Bao－wen，Zhou Yu－ming，et al.New random testing－based fault localization approach［J］.Computer Science，2013，40（1）：5－14.（in Chinese）

［13］ Wang Jian－wu.Introduction to mathematical thinking method［M］.Hefei：Anhui Education Press，1996.（in Chinese）［14］ Wang Zhen－zhen.Construction of knowledge database of naïve fuzzy description logic and naïve reasoning［J］.Applied Science and Technology，2012，39（6）：18－29.（in Chinese）

附中文参考文献：

［12］ 王蓁蓁，徐宝文，周毓明，等.一种随机TBFL方法［J］.计算机科学，2013，40（1）：5－14.

［13］ 王健吾.数学思维方法引论［M］.第1版.合肥：安徽教育出版社，1996.

［14］ 王蓁蓁.朴素模糊描述逻辑知识库构造及其朴素推理［J］.应用科技，2012，39（6）：18－29.