两个自认证签密方案的攻击及改进*
2014-03-23王云
王 云
(青海大学成人教育学院,青海西宁810001)
1 引言
我们的社会已经进入了一个崭新的时代,传统商务、事务处理、政府服务越来越多地需要通过计算机和通信网络来实现,而只有在开放网络能提供安全通信的前提下,上述事务才能实现。如何在开放网络中保证通信的安全性,就是利用密码技术。签密技术和自认证公钥技术是密码学中两种新的密码技术。签密技术能在一个逻辑步骤内完成数字签名和加密两项功能[1]:自认证公钥技术使得用户的公钥无需被单独认证,而且用户的私钥由用户自己独立生成,密钥生成中心PKG无法假冒用户。两种密码技术的相互结合,便出现了许多自认证签密方案[2~5]。
本文对俞惠芳、王彩芬[6]提出的一个高效的自认证签密方案和王之仓等[7]提出的基于离散对数问题的签密方案进行分析研究,发现这两个方案存在安全隐患。存在已知明文与密文对的伪造攻击:即任意第三方可借助窃取到的明文与密文对假冒发送方伪造任意消息的签名。进而对文献[6]提出改进,改进后的方案既保留了原方案的优点又有效克服了原方案的不足。通过新旧方案的分析对比表明:改进的方案具有通信成本低、计算效率高、安全性强、算法简单等优点。
2 预备知识——双线性映射
设G1为q阶加法循环群,G2为q阶乘法循环群,在G1和G2上计算离散对数为困难问题。称e:G1×G2→G2为G1到G2双线性映射,如果满足下述条件:
双线性:对任意P、Q∈G1,a、b∈Z*q,e(aP,b Q)=e(P,Q)ab成立。
非退化性:∃P、Q∈G1满足e(P,Q)≠1。
可计算性:对任意的P、Q∈G1,存在一个有效算法计算e(P,Q)。
3 文献[6]方案介绍及其改进
3.1 文献[6]方案介绍
3.1.1 系统设置
(1)G1、G2是可信机构CA选择的两个阶为q(q为素数)的循环群,其中,G1为加法群;G2为乘法群;p为G1的生成元。e是G1×G2→G2的双线性映射。
(2)定义三个密码学上安全的哈希函数:
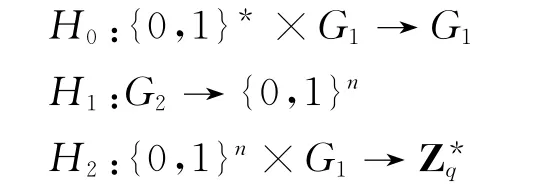
(3)CA选取s∈R作为系统主密钥,计算PCA=sp作为其公钥。
(4)保密系统主密钥s,公开系统参数:{G1,G2,q,e,p,n,H0,H1,H2}。
3.1.2 用户密钥的提取
身份为IDA的签密者A选择秘密值rA∈R,并计算PA=rAp。然后签密者A发送(IDA,PA)给CA。CA收到(IDA,PA)后,计算QA=H(IDA,PA)和xA=sQA,并将(IDA,QA,XA)发送给签密者A。签密者A收到(IDA,QA,XA)后,可通过验证方程e(xA,P)=e(QA,PCA)是否成立来检验xA的合法性。如果上式成立,则签密者就接受xA作为自己的部分私钥,计算SA=rAQA+xA作为自己的私钥,并将pA作为自己的公钥。接收者B的部分私钥以及公私钥对(xB,PB,SB)可采用相似的方法获得。
3.1.3 签密
签密者A发送消息m给接收者B,执行以下步骤:
(1)选择k∈R,计算R=kp;
(2)计算V=e(QB,PB+PCA)k,c=H1(V)⊕m;
(3)计算S=H2(m,R)SA;
(4)输出密文组σ=(R,c,S)。
3.1.4 解签密
B收到密文(R,c,S)后,执行以下步骤:
(1)计算V=e(R,SB)。
(2)恢复消息m=c⊕H1(V)。
(3)检查等式e(P,S)=e(QA,PA+PCA)是否成立。如果等式成立,签密(R,S)和公钥PA同时被验证,B接收(R,S);否则,验证失败,认为(R,S)不合法。
3.2 文献[6]的分析
假设O窃取A向B发送的已知消息m的一组密文(R,c,S),则O可假借A的名义向B发送任意消息m′的合法密文组(R′,c′,S′),具体过程如下:
(1)选择r0∈R,计算R′=r0R;
(3)计算S′=S*H2(m′,R′)H2(m,R)-1;
(4)输出密文组σ=(R′,c′,S′),则密文组(R′,c′,S′)也是合法密文。正确性证明过程如下:
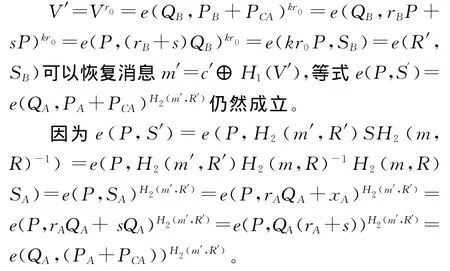
3.3 文献[6]的改进方案
除签名和验证步骤外,与原方案相同的部分不再重复,以下只列出签名和验证过程。
3.3.1 签名过程
(1)选择k∈R,计算R=kp,R′=kQA;
(2)计算V=e(QB,PB+PCA)k,c=H1(V)⊕m;
(3)计算S=H2(m,R)kSA;
(4)输出密文组σ=(R,R′,c,S)。
3.3.2验证过程
恢复消息后,检查等式e(P,S)=e(R′,PA+PCA)是否成立。如果等式成立,签密(R,S)和公钥PA同时被验证,B接收(R,S);否则,验证失败,认为(R,S)不合法。
3.3.3 文献[6]与改进方案的仿真结果对比
针对文献[6]可取q=12347,a=2,p=11,rA=7,s=5,QA=13,则pA=77,XA=65,SA=156,则签名者A的部分私钥和公私钥对为(65,77,156);同理rB=17,QB=19,则PB=187,XB=95,SB=418,签名者B的部分私钥和公私钥对为(95,187,418),签名者A对消息m签名,取k=2,则R=22,v=e(QB,PB+PAC)3,c=H1(v)⊕m,H2(m,R)=4,s=624,假设第三者O已经成功窃取已知消息m的一组签名(22,{0,1}m,624),O可轻易获得签名者A的私钥SA=624*4-1=156。可对任意消息M′进行签名,取r0=3,R′=66,V′=V3,c′=H1(v′)⊕M′,H2(m′,R′)=6,则S′=936,这一组数据满足签名方程,是合法数据。
针对改进方案同样取上述数据,即签名者A的部分私钥和公私钥对为(65,77,156),签名者B的部分私钥和公私钥对为(95,187,418),假设第三者O已经成功窃取已知消息m的一组签名(22,{0,1}m,624),由于签名方程中含有未知数k,无法进行伪造,只能猜测,但猜测成功的概率只有1/12347,可以忽略不计。要使得方案更加安全,只需q取更大的数即可。
3.4 改进方案的安全性分析
改进的方案在不额外增加参数的前提下,将秘密随机值k巧妙加入到签名方案中,只增加了两次数乘运算,就保证了签名方案的安全性能。因为任何人想从R、R′得出参数k的值是不可行的,这相当于解决ECDL问题,而签名方案中必须要知道参数k的值,故攻击者无法获得关于消息的任何有用信息。即使有人得到了消息的明文和密文对,要想进行伪造签名也是不可能的。因为签名方程中添加了参数k,k对攻击者来说是不可能知道的。所以改进方案的安全性大大加强,效率也非常高,同时也满足原签名方案的其他特性。
3.5 文献[7]的介绍及分析
文献[6]签名方案中关键的一步,即S=H2(m,R)SA中没有其它参数,只有签名者的私钥SA和H2(m,R)两项乘积。相似方案都存在类似的安全隐患,如文献[7]。别的不再多述。
3.5.1 系统初始化
PKG选择两个大素数p1和q1,并满足p1=2p′+1,q1=2q′+1,其中p′、q′也是大素数。计算p=p1q1,并选择一个阶为p′q′的生成元g和一个安全的可变长的单向哈希函数H。随机选择一个秘密值s∈作为主密钥,计算其公钥y=gsmod p,最后,保密p1、q1、p′、q′、s,公开p、g、H和y。
3.5.2 用户注册
身份为du的用户u选择一个秘密值ru∈R,计算yu=grumod p,然后用户发送(du,yu)给PKG。PKG计算Qu=H(du,yu)和xu=gsQu,并将(Qu,xu)发给用户u。用户u收到后,验证方程yQu=xumod p检验xu的合法性。若上式成立用户就计算Su=ruH(xu)作为自己的私钥,yu作为自己的公钥。签密者和密文接收者相应的身份、部分私钥、公钥以及私钥分别简记为(dA,xA,yA,SA)和(dB,xB,yB,SB)。
3.5.3 签密
签密者A发送消息m给接收者B,执行以下步骤:
(1)选择k∈R,计算R=gkmod p;
(3)计算S=H(m,R)g-kgSAmod p;
(4)输出密文组σ=(R,c,S)。
3.5.4 解签密
B收到密文(R,c,S)后,执行以下步骤:(1)计算V=RSB mod p。
(2)恢复消息m=c⊕H(V)。
假设O已成功窃取A向B发送的已知消息m的一组密文(R,c,S),则O可假借A的名义向B发送任意消息m′的合法密文组(R′,c′,S′),具体过程如下:
(1)选择r0∈R,计算R′=Rr0 mod p;
(3)计算S′=S*H2(m′,R′)R-r0 RH(m,R)-1;
(4)输出密文组σ=(R′,c′,S′),则密文组(R′,c′,S′)也是合法密文。正确性证明过程如下:
由原方案可知,V=RSB mod p,则V′=Vr0 mod p=Rr0 SB mod p=R′SB mod p;
4 结束语
本文对俞惠芳等提出的一个高效的签密方案和王之仓等提出的一个基于离散对数的签密方案的安全性进行了研究分析,发现这两个方案的相似之处,即类似方案均存在已知明文与密文对的伪造攻击,进而对其进行改进。通过添加随机参数的方法,恰倒好处地克服了原方案的安全隐患,相比现行签密方案更加安全有效。如何将其应用在现今飞速发展的电子商务和电子政务中将是今后的一个重点研究方向。
[1] Zheng Yu-liang.Digital signcryption or how to achieve cost(signature &encryption)≪cost(signature)+cost(encryption)[C]∥Proc of Cryptology,CRYPYO’97,1997:165-179.
[2] Geng Li,Wang Shang-ping,Zhou Feng,et al.A new ID-based signcryption scheme[J].Computer Engineering,2004,30(19):52-54.(in Chinese)
[3] Bao Feng,Deng R H.A signcryption scheme with signature directly verifiable by public key[C]∥Proc of Cryptography,PKC’98,1998:55-59.
[4] Yum D H,Lee P J.New signcryption schemes based on KCDSA[C]∥Proc of ICISC’01,2001:305-317.
[5] Girault M.Self-certified public keys[C]∥Proc of Advances in Cryptology-EUROCRYPT’91,1991:491-497.
[6] Yu Hui-fang,Wang Cai-fen.An efficient self-certified signcryption scheme[J].Computer Engineering,2009,35(16):138-142.(in Chinese)
[7] Wang Zhi-cang,Yu Hui-fang.Self-certified signcryption scheme based on discrete logarithm problem[J].Computer Applications and Software,2010,27(10):223-225.(in Chinese)
附中文参考文献:
[2] 耿莉,王尚平,周峰等.一种新的基于身份的签密方案[J].计算机工程,2004,30(19):52-54.
[6] 俞慧芳,王彩芬.一个高效的自认证签密方案[J].计算机工程,2009,35(16):138-142.
[7] 王之仓,俞慧芳.基于离散对数问题的自认证签密方案[J].计算机应用与软件,2010,27(10):223-225.
