基于多配置LFSR的测试生成结构设计＊

李 鹏，颜学龙，孙 元

（桂林电子科技大学电子工程与自动化学院，广西桂林541004）

1 引言

当今深亚微米和超亚微米技术已成为集成电路设计的主要工艺，集成电路的测试开销已经直接影响到了系统的总开销。内建自测试BIST（Build－In Self－Test）是解决大型复杂电路的有效方法［1～3］，其中测试矢量生成器则是决定BIST测试质量的重要组成部分，优质的测试矢量生成器不仅可以用较短的时间获得较高故障覆盖率，而且硬件开销较少。许多学者已经对测试生成方法提出了各自的观点，如早期的测试生成方法有确定性测试方法、穷举/伪穷举测试方法、伪随机测试方法等［1，4］，它们都在测试集长度、测试存储、故障覆盖率、硬件开销等方面存在各种缺陷，近年来一些新兴的测试生成方法对上述问题做了很大程度上的改进，如加权测试生成法［5，6］通过调整被测电路输入引脚信号‘0’、‘1’信号出现的概率，以提高故障覆盖率，但这种方法对于被测对象内部结构已知的电路能取得比较好的效果，若被测对象内部结构未知，则各输入端的权重无法准确获得，因此测试不具备普遍性；又如文献［7］提出的压缩确定性矢量集的方法，虽可以有效地减少测试时间、提高故障覆盖率，但压缩的矢量集需要存储机制，这样又是以增加硬件开销为代价。再如文献［1］提出的基于线性反馈移位寄存器LFSR（Linear Feedback Shift Register）结构优化和初态选择的混合测试矢量生成；文献［8，9］提出的LFSR重复播种的测试方法以及文献［10］提出的受控LFSR，都是通过选择部分有针对性的测试矢量，以减小测试冗余，提高故障覆盖率。但是，这些结构都是需要借助特定的算法和一定的硬件结构来完成矢量的生成。

本文综合考虑硬件开销和故障覆盖率等因素，提出一种多配置LFSR的混合测试生成结构及其反馈配置生成的优化算法。该结构无须存储测试矢量，直接通过对LFSR反馈网络的配置和分时段控制，就能用较小的硬件代价实现随机性矢量和确定性矢量的生成。因此，被测电路中的随机矢量可测性故障（Random Pattern Detectable Faults）和抗随机性故障（Random Pattern Resistant Faults）均能够被检测［11，12］，从而提高了单位时间内的故障覆盖率。

2 可配置LFSR结构及随机性测试矢量生成

图1为可配置反馈网络LFSR的结构图，其各个触发器的输入是由触发器输出经反馈异或配置串联选择反向配置（合并称“反馈配置”）得到。该电路的各个输入Vi可用含有r个触发器输出的逻辑变量QL1（n），QL2（n），…，QLr（n）和反向配置逻辑变量Ci表示成二元域内的线性非齐次方程：

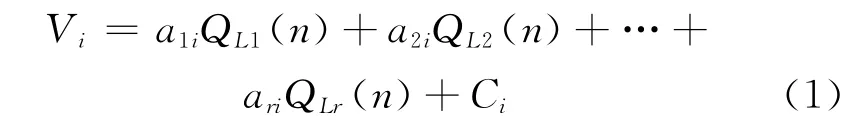
其中，aki为第k个触发器反馈接入第i位输入的配置节点，aki∈｛0，1｝，k、i＝1，2，…，r。aki＝1时表示反馈接入异或门，反之表示无反馈接入；Ci为非门控制，Ci∈｛0，1｝，Ci＝1时表示通过非门接入输入，反之则直通输入；QLi为第i位触发器输出。

相对于传统的外异或LFSR结构（如图2所示），本结构将各个触发器的输出经过异或非配置后导入到各个触发器的输入，如此可以生成比传统LFSR更优质的测试序列［13］。传统LFSR的特征多项式为式（2），它的各项系数反映了LFSR各阶节点的反馈配置，同时结合各触发器的初值，就可以得到状态更新序列，即状态矩阵方程（3）中表达式QL1（n＋1）的值：

Figure 1 Configurable LFSR structure图1 可配置LFSR结构图

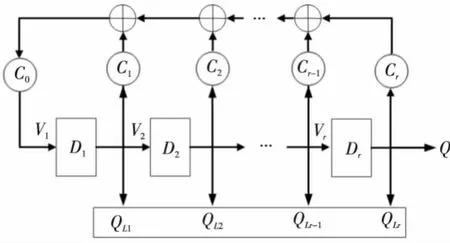
Figure 2 External XOR LFSR structure图2 外异或LFSR结构

其中QLi（n）表示触发器在第i时刻的值，QLi（n＋1）表示在i＋1时刻的值，B为LFSR的状态转移矩阵［13］。由此可知，除了第一位V1的输入是由反馈配置而成，其余各位均由第一位移位得到。

因此，只要确定LFSR的初始状态和反馈配置，那么它生成的测试矢量就是固定的。若该多项式是r次的本原多项式［1］，就可以产生具有最长周期（2r－1个）的伪随机测试矢量，并从各触发器的输出端并行导出。

如果将式（1）中的Ci全部清0，aki配置成式（3）中的状态转移矩阵（i＝1，2，…，r），那么就生成和传统LFSR一样的伪随机测试矢量。

图3为可配置LFSR结构生成随机性测试矢量的仿真波形。

此外，对于确定性矢量的生成，按其产生的顺序，将待生成的测试矢量的第i位，从第1个序列到第s个序列依次代入到方程（1）中，即可得到矩阵方程（4）：

对应于式（4）中的各个部分，可简记为：b＝A＊CNi，其中b为确定性矢量在第i位的次态值列向量，CNi为配置列向量，A中的Vxi为确定性矢量的现态值，s为确定性测试集的大小。如果方程（4）有解，说明该确定性测试集的第i位序列可以完全通过配置向量CNi得到；反之，说明该配置向量只能生成原确定性测试集在第i位中的一部分序列，而另一部分需要重新代入式（1），构造新的矩阵方程，寻求新的配置向量，直到全部测试集可解为止。因此，生成完整的确定性测试集可能需要多种配置。

3 多配置LFSR结构及确定性测试集的生成

在可配置LFSR的基础上，将随机性测试矢量配置和各个确定性测试矢量配置分时段作用于触发器阵列上，就得到如图4所示的多配置LFSR结构。

3.1 确定性测试矢量的划分

在多配置的LFSR结构中，完整的确定性测试集被划分为p个子集，每个子集由相应的配置向量作用一定的时钟来生成。其中配置通道的个数和配置向量的作用时钟都需要通过对原测试矢量的划分来决定，矢量划分的理论基础就是非齐次方程组的有解判定定理［14］。

Figure 4 Multi－configurable LFSR图4 多配置LFSR结构

定理1 非齐次线性方程组：

Figure 3 Simulation waveform of random test vectors图3 随机性测试矢量的仿真波形

则式（5）可写成Ax＝b。方程组（5）有解的充分必要条件是矩阵A的秩R（A）等于其增广矩阵的秩R（A｜b）。

定理2 设η是非齐次方程组的一个特解，ξ1，ξ2，…，ξn－r是其导出组的基础解系，则非齐次方程组（5）的通解为η＋k1ξ1＋k2ξ2＋…＋kn－rξn－r，其中r＝R（A），k1，k2，…，kn－r为任意常数。

推论 若R（A）＝R（A｜b）＝n，方程组（5）有唯一解；若R（A）＝R（A｜b）＜n，方程组（5）有无穷多解，其通解为η＋k1ξ1＋k2ξ2＋…＋kn－rξn－r；若R（A）≠R（A｜b）时，方程组（5）无解。

根据上述的定理1和推论可知：方程组（4）中只有当R（A）＝R（A｜b）时，才可以求出其配置向量CNi；若R（A）≠R（A｜b），则需要对原测试集进行划分，划分的步骤为：

（1）将方程组（4）中的增广矩阵（A｜b）做行初等变换（二元域内的模2加），使每行第一个非零元素下面的数为0。

（2）找出增广矩阵（A｜b）中A阵全为0、而b中不为零的行，即是R（A）≠R（A｜b）的行，那么该行便是原测试集的一个划分点。

（3）将原测试集在该划分点之后的测试矢量重新代入方程（4），并重复步骤（1）、（2），直到剩余的测试矢量全部可解。

划分子集的个数即为配置向量通道的个数p，而各划分子集的长度（子集中包含测试矢量的个数）就是每个配置向量的作用时钟数。

3.2 单输入位的优化配置

根据定理2可知，非齐次方程可能存在多组解，而解结构的不同，整个结构的硬件开销也随之不同，因此为了获得较少的硬件开销，必须对方程的通解进行寻优。对于配置向量CNi＝（a1ia2i…ariCi），其中各个元素取值为0或1，向量中的“1”元素对应着配置网络中的门结构的连接，因此要使门结构最少，应以寻找通解中“1”最少的一组解向量作为限制条件，进行解空间内的寻优。寻优步骤为：

（1）求出矩阵方程的基解（ξ1ξ2…ξN）和特解η。

（2）将基解矩阵（ξ1ξ2…ξN）T做初等行变换［15］，使每行第一个非0元素以下和以上的各行对应元素为0，得（ξ′1ξ′2…ξ′N）T。

（3）计算η中含“1”的个数，记I（η），并在ξ′1ξ′2…ξ′N中找出与η重复度最大的基ξ′r1，做运算η1＝η⊕ξ′r1。

（4）计算I（η1），并比较I（η）和I（η1）。若I（η）＜I（η1），则η即为最优通解，算法停止；若I（η）≥I（η1），则在余下的ξ′1，ξ′2，…，ξ′r1－1，ξ′r1＋1，…，ξ′N中找出与η1重复度最大的基ξ′r2，重复（3）、（4）两个步骤。

在通解寻优过程中，若采用遍历算法，则需要用特解η与所有基解（ξ1ξ2…ξN）进行2N次组合，再在这些组合当中寻找含‘1’最少的通解作为最优配置解，然而对于基解个数较多的矩阵方程，无疑大大增加了寻优复杂度。而通过本文提出的算法能够快速地寻找最优通解配置，其中初等行变换过程包括由上至下和由下至上，至多需要进行N×（N＋1）次更新；特解的更新过程至多需要进行N次，因此最大寻优次数不超过N×（N＋2）次。

3.3 全部输入位的优化配置

式（4）仅指出了第i位的配置向量，将各位（i＝1，2，…，r）代入式（4）中并列出矩阵方程，即为式（6）。

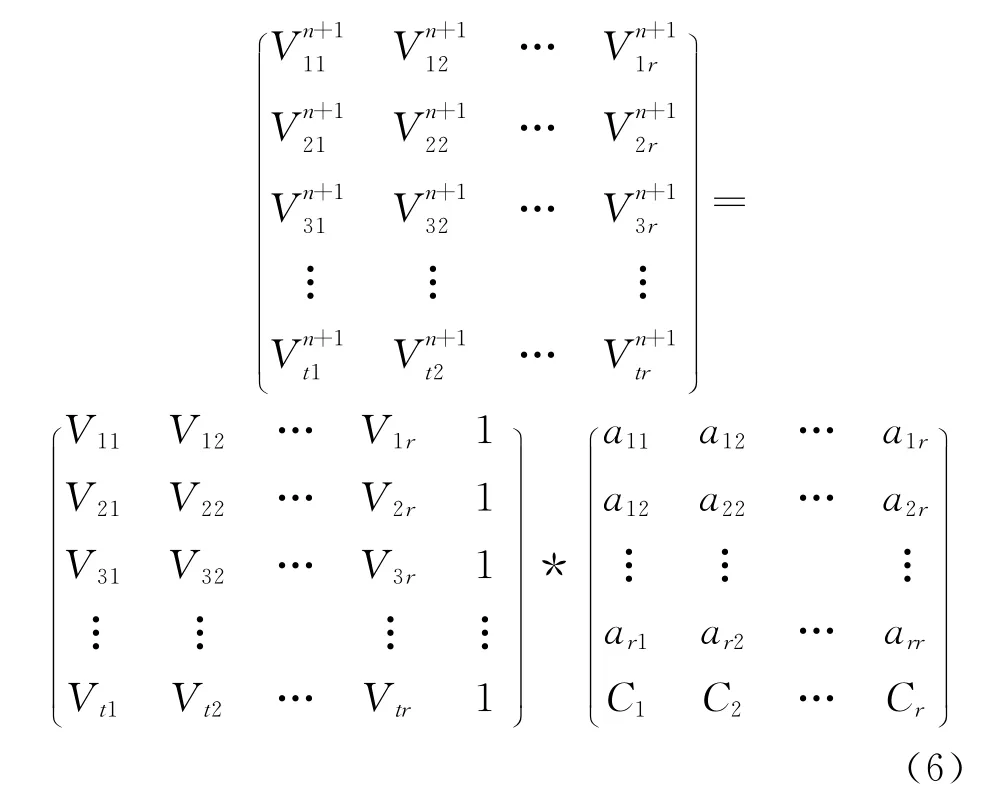
对应式（6）中的各个部分简记为：B＝A＊Con，B为确定性矢量的次态值，A中的Vmn部分为现态值，Con为所有位的反馈配置矩阵，下标t为确定性测试集的大小减1。将这里的增广矩阵A｜B做如同3.1节中的矢量划分处理；再解出各个子集的通解配置向量，并按3.2节中的寻优算法遍历全部配置位；最后结合子集的长度，一起施加到可配置LFSR结构就可生成各确定性子集。

4 配置优化实例

为了验证方案的可行性，以文献［16］中一组六位测试矢量为例，如表1所示，将表1的序列1到序列15代入到式（6）中的现态矩阵A的Vmn中，序列2到序列16代入到次态矩阵B中，列出矩阵方程为式（7）。对式中的增广矩阵A｜B做矢量划分，式中用虚线绘出，解出各个子集，并对配置解向量进行优化。表2列出了本文提出的方案和文献［16］优化结果比较。表2中简记表达式a1iV1D＋a2iV2D＋…＋ariVrD＋Ci为配置向量CNi＝（a1ia2i…ariCi）。表2最后一行的硬件占用面积由公式（8）［16］计算得到，其中W1为二输入异或门（XOR）的硬件面积，W2为非门（NOT）的硬件面积，W3为触发器（FFA）的硬件面积，取W1＝11.52μm2，W2＝4.32μm2，W3＝38.88μm2。

Table 1 Deteministic test vectors in reference［16］表1 文献［16］中的确定性测试序列

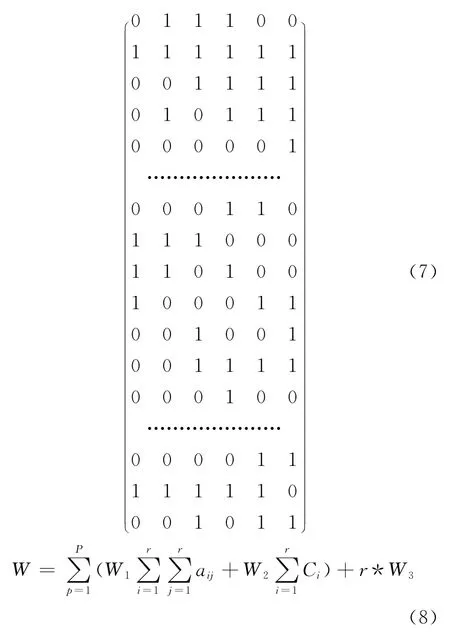
由此可看出，本文的方案在生成各个子序列时，对配置网络使用的硬件开销有更进一步的减小。

在Quartus II环境下，编写多配置的LFSR结构，并将上述反馈配置向量加载到结构中，得到如图5所示的确定性测试集的仿真波形。

表3和表4分别列出了文献［16］和本文对几种综合基准电路的矢量划分和硬件开销的比较结果。

实验所用到的确定性矢量由文献［17］提供，矢量集大小以文献［16］提供的大小为基准，实验使用C代码模拟各个矢量集划分和各个子集所需的配置网络的生成过程。

由比较结果可以看出，本文提出的方法在硬件开销方面，异或门的数量有显著减少，非门数量也有一定程度的减少，因此在总体硬件面积方面本文所提方法更具有优势。

Figure 5 Simulation waveform of determistic test vectors图5 确定性测试集的仿真波形

Table 2 Comparison of configuration vectors results in reference［16］with this paper表2 文献［16］和本文配置向量的比较结果

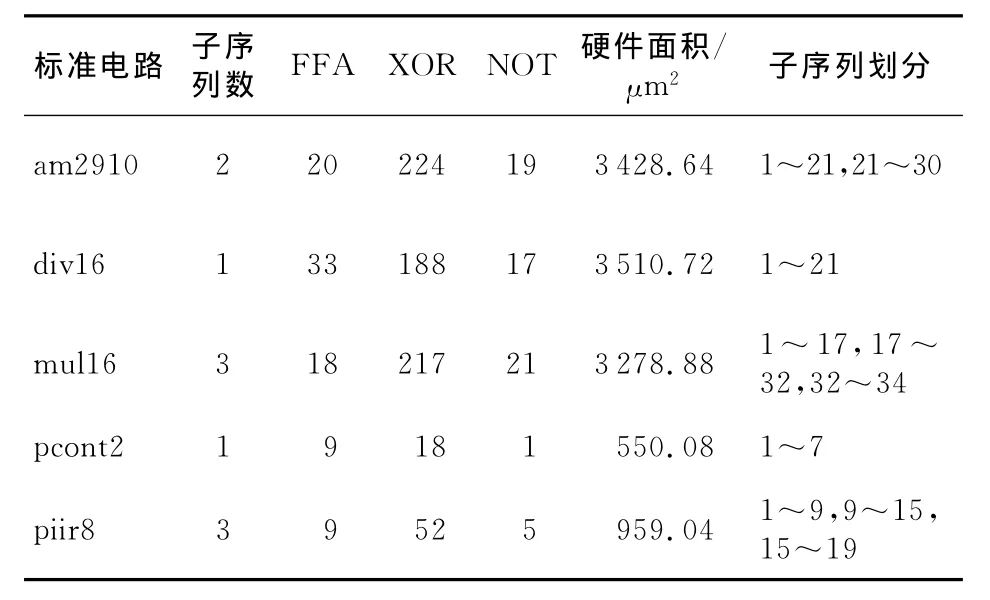
Table 3 Optimization results in reference［16］表3 文献［16］优化的结果

Table 4 Optimization results in this paper表4 本文优化的结果

5 结束语

本文介绍了一种多配置LFSR的测试生成结构，该结构通过实时地配置反馈网络，可以实现随机性测试矢量和确定性测试矢量的生成。在配置确定性测试矢量时，利用矩阵的相关理论，提出了一种对原始序列进行划分的方法和一种寻求各划分子序列的最优配置向量解的优化算法，算法实现简易可靠。通过实例和对几种综合基准的验证，证明了本方案能生成任意给定的测试矢量，同时能更大程度地减少硬件开销。

致谢

感谢数学与计算机科学学院的段复建老师，在本文的“单输入位的优化配置”一节中，对通解的优化算法提供的指导和帮助。

［1］ Xie Yong－le，Sun Xiu－bin，Wang Yu－wen，et al.A mixed mode BIST approach of digital integrated circuits［J］.Chinese Journal of Scientific Instrument，2006，27（4）：367－375.（in Chinese）

［2］ Zhou Bin.Research on low cost deterministic Built－In Self－Test（BIST）［D］.Haerbin：Harbin Institute of Technology，2010.（in Chinese）

［3］ Li Xin，Liang Hua－guo，Chen Tian，et al.Low power deterministic built－in self－test based on folding counter［J］.Chinese Journal of Scientific Instrument，2011，32（12）：1－5.（in Chinese）

［4］ Yang Ji－xiang.Data domain test technology and instruments［M］.Beijing：Science Press，1990.（in Chinese）

［5］ Xie Yong－le，Chen Guang－ju.Deterministic test set based random test with multiple weighted set of digital integrated circuits［J］.Chinese Journal of Scientific Instrument，2002，23（6）：576－578.（in Chinese）

［6］ Tan En－min.Optimizing methods in the design of build－in self－test for digital circuits［D］.Shanghai：Shanghai Jiaotong University，2007.（in Chinese）

［7］ Rozkovec M，Jenicek J，Novak O.Application dependent FPGA testing method using compressed deterministic test vectors［C］∥Proc of the 16th IEEE International on On－Line Testing Symposium，2010：192－193.

［8］ Yang Yi，Zhou Rui－hua，Huang Wei－kang.On reseeding BIST schemes with variable lengths of test sequences［C］∥Proc of CTC’04，2004：215－221.（in Chinese）

［9］ Yong Zhi－yan，Hong Wang，Zhi Jia－yang，et al.A new LFSR reseeding method for BIST［C］∥Proc of the 8th IEEE International Conference on Solid－State and Integrated Circuit Technology，2006：2145－2147.

［10］ Hu Chen，Xu Ge－fu，Zhang Zhe，et al.BIST structure and test vector generation based on a controlled LFSR［J］.Journal of Circuits and Systems，2002，7（3）：13－16.（in Chinese）

［11］ Yuan X，Chen C I H.Automated synthesis of a multiple－sequence test generator using 2－D LFSR［C］∥Proc of the 11th Annual IEEE International ASIC Conference.1998：75－79.

［12］ Chen C I H，George K.Configurable two－dimensional linear feed back shifter registers for parallel and serial built－in self－test［J］.IEEE Transactions on Instrumentation and Measurement，2004，53（4）：1005－1014.

［13］ Gu Xiao－chen，Zhang Min－xuan.Multi－output fibonacci type LFSR based uniform random number generator：Design and analysis［J］.Computer Engineering ＆Science，2009，31（A1）：80－83.（in Chinese）

［14］ Yang Gui－yuan.Linear algebra［M］.Beijing：Electronic Science and Technology Press，2002.（in Chinese）

［15］ Wang Xing－quan.The essence of row－simplest form and a new proof of its uniqueness［J］.Journal of Hexi University，2010，26（5）：31－34.（in Chinese）

［16］ Zhang Xin－hui，Chen C I H，Ckhakravarthy A.Structure design and optimization of 2－D LFSR－based multi－sequence test generator in built－in self－test［J］.IEEE Transactions on Instrumentation and Measurement，2008，57（3）：651－663.

［17］ Index of VLSI prj benchmarks synthesized［EB/OL］.［2013－05－10］.http：∥service.felk.cvut.cz/vlsi/prj/Benchmarks/Synthesized.

附中文参考文献：

［1］ 谢永乐，孙秀斌，王玉文，等.数字集成电路的混合模式内建自测试方法［J］.仪器仪表学报，2006，27（4）：367－375.

［2］ 周彬.低测试成本的确定性内建自测试的研究［D］.哈尔滨：哈尔滨工业大学，2010.

［3］ 李鑫，梁华国，陈田，等.基于折叠计数器的低功耗确定BIST方案［J］.仪器仪表学报，2011，32（12）：1－5.

［4］ 杨吉祥.数据域测试技术及仪器［M］.北京：科学出版社，1990.

［6］ 谈恩民.数字电路BIST设计中的优化技术［D］.上海：上海交通大学，2007.

［8］ 杨懿，周瑞华，黄维康.变长序列重复播种内建自测试方案探讨［C］∥第三届中国测试学术会议，2004：215－221.

［10］ 胡晨，许舸夫，张哲，等.一种基于受控LFSR的内建自测试结构及其测试矢量生成［J］.电路与系统学报，2002，7（3）：13－16.

［13］ 谷晓忱，张民选.多输出外部反馈型LFSR均匀分布随机数生成器的分析与设计［J］.计算机工程与科学，2009，31（A1）：80－83.

［14］ 杨桂元.线性代数［M］.北京：电子科技出版社，2002.

［15］ 王兴泉.行最简形矩阵的实质及其唯一性的新证明［J］.河西学院学报，2010，26（5）：31－34.