自锚式悬索桥纵向地震响应控制分析

， ，

(1.同济大学 桥梁工程系，上海 200092；2.台州市沿海高速工程建设指挥部，浙江 台州 318000)

随着城市桥梁对景观要求的不断提高，自锚式悬索桥[1-2]的建设也越来越多。自锚式悬索桥不仅具有传统悬索桥造型优美、外观新颖的特点，同时它省去了庞大的锚碇系统，因此更加能够适应城市土地资源紧张或场地地基水平承载能力低的要求。悬索桥结构体系轻柔，地震作用下主梁纵桥向位移很大，需要引入一种合理有效的耗能装置来控制其梁端位移[3]。目前，国内外常用的耗能装置[4-6]主要有铅芯橡胶支座、高阻尼橡胶支座、摩擦摆式支座、液体黏滞阻尼器、金属弹塑性阻尼器等。对于安装黏滞阻尼器的减震结构，与安装其他类型的耗能装置(黏弹性、摩擦性等)的减振结构相比，其最大的优点是原结构的动力特性不会受到影响，而它只是通过改变原结构的整体阻尼比来使结构的动力反应降低。因此，本文选用液体黏滞阻尼器，通过改变阻尼器的控制参数(C,α)对一座双塔自锚式悬索桥纵桥向的地震反应进行控制分析。

1 液体黏滞阻尼器

针对液体黏滞阻尼器的性能和其对结构的减震效果，自上世纪80年代开始Coustantious等美国学者先后进行了大量的振动台试验并发表了大量相关文献[6-8]。目前，阻尼器已被广泛应用于新桥建设和旧桥加固当中。液体黏滞阻尼器一般由缸体、活塞和阻尼材料组成，活塞在缸体内可做往复运动，活塞上有适量小孔，缸体内装有黏滞阻尼材料。地震时，与结构共同工作的黏滞阻尼器的导杆受力，推动活塞运动，活塞两边的阻尼材料产生压力差，阻尼介质通过阻尼孔，产生阻尼力，达到耗能减震的目的。其力学计算模型如下

F=Cvα(1)

式中，C为阻尼系数；v为相对运动速度；α为阻尼指数(通常可取0.1～2，在土木工程领域一般取0.1～1)。

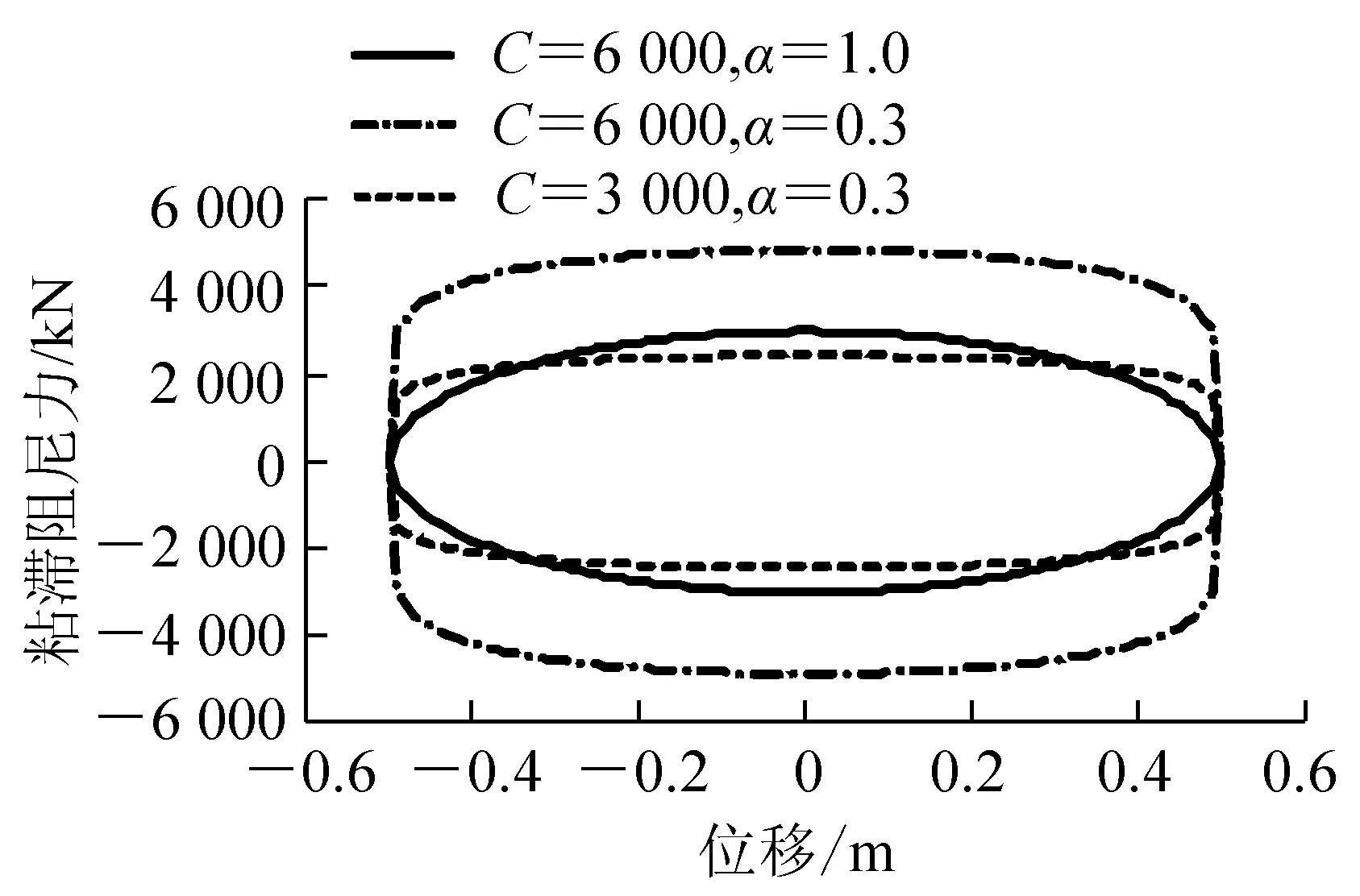
图1 阻尼器力-位移滞回曲线

图1绘制了3种不同参数(C,α)组合的阻尼器在简谐荷载作用下的力-位移滞回曲线。阻尼指数α=1的阻尼器称为线性阻尼器，其滞回曲线形状为椭圆；阻尼指数α≠1的阻尼器为非线性阻尼器，图1绘制了α=0.3时的滞回曲线，其形状跟接近于矩形，并且滞回曲线的面积比线性阻尼器大很多。阻尼系数C的变化对阻尼器的滞回曲线的影响可以从图1中清楚地看出。

2 工程概况与分析模型

2.1 工程背景

该桥为双塔空间索面自锚式悬索桥，跨径布置为40+100+266+100+40 m，主缆矢跨比1/5。主跨跨度266 m，边跨跨度100 m，边主跨比1/2.66，为了克服边墩负反力，边跨再延伸出一跨(锚跨)，全桥总体布置见图2。其中主跨和边跨的主梁为叠合梁，锚跨主梁采用钢筋混凝土箱梁，并在主缆锚固附近设钢混过渡段。索塔为混凝土结构，总高度82 m，在中间设置三道横梁将索塔分为下塔柱、中塔柱、上塔柱和塔冠四部分。其中桥面以上塔高69 m，下塔柱高8.6 m，中塔柱高22.9 m，上塔柱35.4 m，塔冠15.1 m。纵向为半漂浮体系，在索塔处纵向分别设置两个粘滞性阻尼器；索塔、过渡墩处设置双向活动支座，锚墩处设纵向滑动、横向固定支座；索塔处设横向抗风支座，限制索塔处主梁横桥向位移。基础采用大直径钻孔灌注桩群桩基础，桩径2 m。

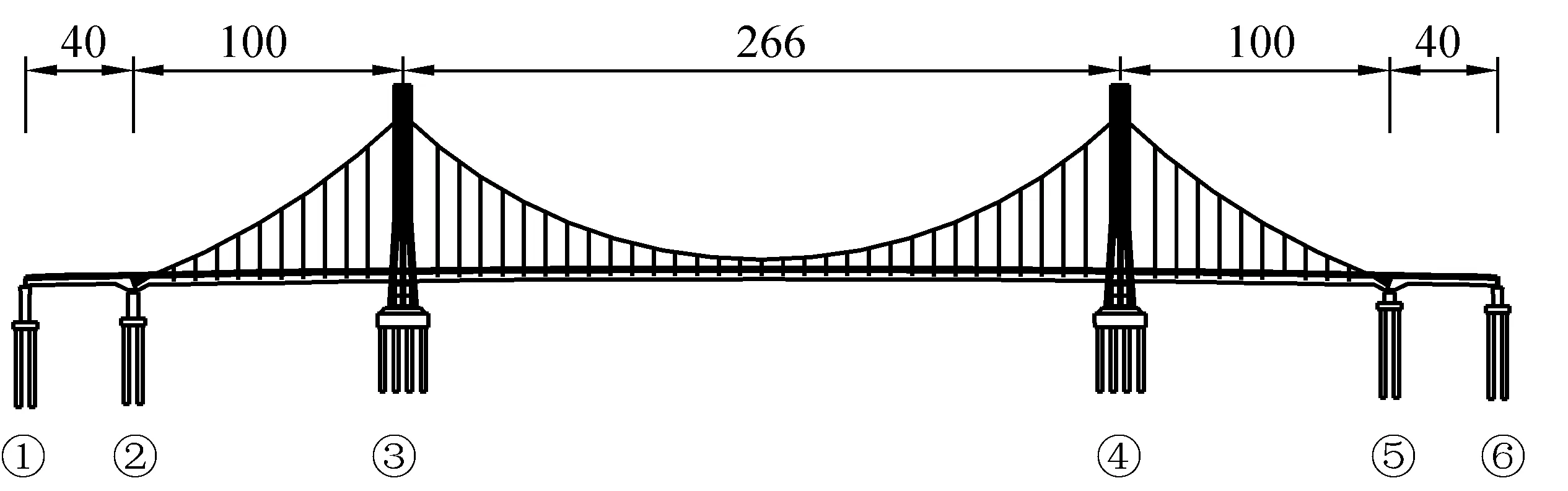
图2 总体立面布置图(单位：m)

2.2 有限元分析模型

采用有限元分析软件SAP2000建立悬索桥的空间动力计算模型。其中，主梁、主塔和桥墩采用空间梁单元模拟，吊索和主缆采用空间桁架单元模拟，由于自锚式悬索桥的主塔和主梁承受很大的轴力，因此考虑了P-Δ效应对主塔和主梁的刚度进行了修正。承台视为刚体，用质点模拟，并与塔底或墩底和桩顶通过主从约束连接。桩基础考虑了群桩效应，通过刚度相互耦合的土弹簧模拟。二期恒载、横隔板等的质量以线质量或点质量的形式施加到结构相应位置。考虑活动球型钢支座的摩擦滑动效应，其力学模型按照库伦摩擦定律计算，即Fy=μN，其中N为支座的恒载竖向反力，μ为摩擦系数，此处取为0.02。

阻尼器通过Damper单元模拟，为了了解不同的阻尼参数(C,α)对纵向地震响应的影响，参考其它已建桥梁[4]并结合本桥的跨径等特点采用了阻尼系数为2 000、2 500、3 000、3 500、4 000，阻尼指数为0.2、0.3、0.4、0.5，总共20种不同阻尼参数组合对本桥进行参数分析。

根据本桥《地震安全性评价报告》提供的3条罕遇地震(50 a超越概率2%)下水平地震动时程函数对该桥进行非线性时程分析。其中，地震动输入方向为纵向+竖向，竖向地震动时程函数取水平向的2/3，方向组合采用SRSS方法，最终结果取3组时程函数计算结果的最大值[9]。

3 纵向地震反应结果分析

针对上述模型进行非线性时程分析，得到20组不同阻尼参数的分析结果。为了比较不同阻尼参数 对关键部位纵向地震反应的影响规律，选取3号桥塔的塔底最不利剪力和弯矩、桩基础最不利单桩剪力和弯矩、塔顶最大位移及主梁最大位移进行了规律总结，并与未采用阻尼器的分析结果进行了比较。同时总结了阻尼器最大出力和最大冲程的变化规律，对阻尼器的选取提供了进一步的参照。

3.1 塔底内力

塔底最不利剪力和弯矩的结果如图3。由图3可知，与未采用阻尼器的情况相比：阻尼参数为(4 000,0.2)时，剪力由38 605 kN降为29 973 kN，降幅最大，为22.4%；阻尼参数为(2 000,0.5)时，剪力由38 605 kN降为32 507 kN，降幅最小，为15.8%；阻尼参数为(4 000,0.2)时，弯矩由1 180 062 kN·m降为585 847 kN·m，降幅最大，为50.4%；阻尼参数为(2 000,0.5)时，弯矩由1 180 062 kN·m降为910 786 kN·m，降幅最小，为22.8%。在采用阻尼器后，随着α增加，地震剪力无显著的变化，α每变化0.1剪力最大改变514 kN，而地震弯矩逐渐增加，α每变化0.1弯矩最大改变45 889 kN·m；随着C的增加，地震剪力有增有减，C每变化500剪力最大改变931 kN，而地震弯矩逐渐减小，C每变化500弯矩最大改变73 352 kN·m，最小改变45 150 kN·m。

图3 塔底地震内力

3.2 塔底单桩最不利内力

塔底最不利桩基内力的结果见图4。由图4可知，与未采用阻尼器的情况相比：阻尼参数为(4 000,0.2)时，剪力由4 729 kN降为3 576 kN，降幅最大，为22.4%；阻尼参数为(2 000,0.5)时，剪力由4 729 kN降为4 169 kN，降幅最小，为11.8%；阻尼参数为(4 000,0.2)时，弯矩由20 140 kN·m降为15 380 kN·m，降幅最大，为23.6%；阻尼参数为(2 000,0.5)时，弯矩由20 140 kN·m降为17 850 kN·m，降幅最小，为11.4%。在添加阻尼器后，随着α增加，地震剪力逐渐增加，但α每改变0.1剪力最大改变量仅为72 kN，地震弯矩逐渐增加， 每改变0.1弯矩最大改变量也仅为300 kN·m；随着C的增加，地震剪力逐渐减小，C每改变500剪力最大改变量为115 kN，地震弯矩逐渐减小，C每改变500弯矩最大改变量为530 kN·m。

图4 塔底单桩最不利内力

3.3 塔顶及主梁位移

塔顶及主梁最大位移结果如图5。由图5可知，与没有采用阻尼器的情况相比：阻尼参数为(4 000,0.2)时，塔顶位移由0.497 m降为0.224 m，降幅最大，为54.9%；阻尼参数为(2 000,0.5)时，塔顶位移由0.497 m降为0.365 m，降幅最小，为26.5%；阻尼参数为(4 000,0.2)时，主梁位移由0.485 m降为0.211 m，降幅最大，为56.5%；阻尼参数为(2 000,0.5)时，弯矩由0.485 m降为0.333 m，降幅最小，为31.5%。采用阻尼器后，塔顶及主梁位移变化趋势与塔底单桩最不利内力相似，C每改变500或α每改变0.1位移变化不大。

图5 塔顶及主梁最大位移

3.4 阻尼器反应

阻尼器最大出力和最大冲程如图6。由图6可知，随着α的增加，阻尼器最大出力逐渐减小，最大冲程逐渐增大；随着C的增加，阻尼器出力逐渐增加，C每改变500其改变量在324～448 kN之间，阻尼器最大冲程逐渐减小，但α每改变0.1引起的改变量逐渐减小，在0.011～0.036 m之间。在阻尼参数为(4 000,0.2)时，阻尼器出力最大为7 252 kN，阻尼参数为(2 000,0.5)时，阻尼器出力最小为1 784 kN；阻尼参数为(2 000,0.5)时，阻尼器冲程最大为0.348 m，阻尼参数为(4 000,0.2)时，阻尼器冲程最小为0.214 m。

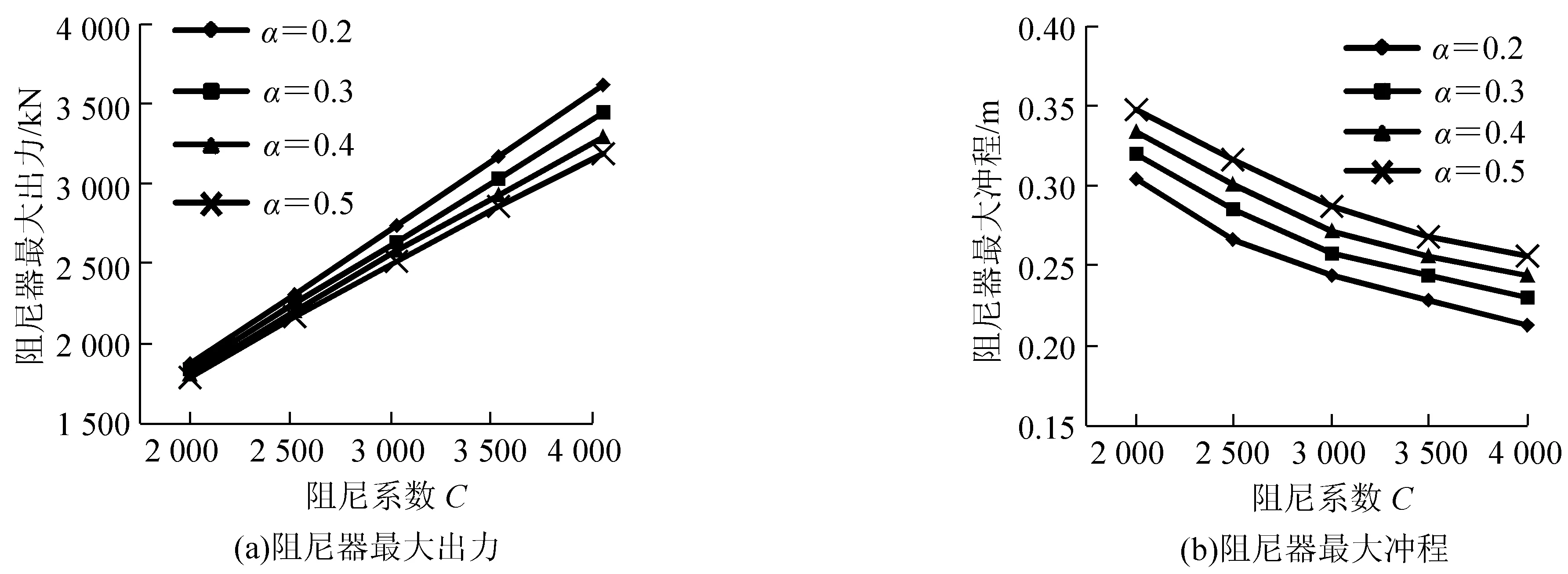
图6 阻尼器最大反应

4 结论

通过以上分析比较可以得出以下结论：

(1)阻尼器对减小塔底内力、塔底桩基内力、塔顶及主梁位移有非常显著的效果。与未采用阻尼器的情况相比，塔底剪力减幅在15.8%～22.4%之间，塔底弯矩减幅在22.8%～50.4%之间，塔底桩基剪力减幅为11.8%～22.4%，塔底桩基弯矩减幅为11.4%～23.6%，塔顶位移减幅达26.5%～54.9%，主梁位移减幅达31.5%～56.5%。

(2)对于不同的阻尼参数C和α，除了塔底地震剪力未呈现处明显变化规律外，塔底弯矩、塔底桩基内力、塔顶及主梁位移，均表现为α越小反应越小，C越大反应越小。但C每改变500引起这些反应的改变量要大于α改变0.1引起的改变量，即改变C值效果更显著。

(3)随着C的增大或α的减小，结构反应逐渐减小，但此时阻尼器的输出力将变大。输出力变大增加了对阻尼器连接构造的要求，同时阻尼器的价格也相应的提高；另一方面国内生产的阻尼器的α值最小仅能达到0.3，采用国外的阻尼器增加了经济成本。综合考虑以上因素，当C取3 500左右，α取0.3时，塔底弯矩减为原来的60%左右，同时主梁位移减为原来的50%左右，对于此桥既能达到满意的减震效果又能节约成本。

参 考 文 献

[1]孟帆超. 悬索桥[M]. 北京：人民交通出版社，2011．

[2]John A Ochsendorf, Divid P Billington. Self- Anchored Suspension Bridges[J] . Journal of Bridge Engineering, 1991, 4(3) ：151-156．

[3]王静．某自锚式悬索桥减震性能研究[J]．石家庄铁道大学学报：自然科学版，2013，26(2)：31-35．

[4]陈永祁. 桥梁工程液体黏滞阻尼器设计与施工[M]. 北京：中国铁道出版社，2012．

[5]庄军生. 桥梁减震、隔震支座和装置[M]. 北京：中国铁道出版社，2012．

[6]Priestley M J N，Seible F，Calvi G M．Seismic design and retrofit of bridges[M]．New York: John Wiley and Sons，1996．

[7]Constantinou M C，Symans M D．Experimental and analytical investigation of seismic response of structures with sup-plemental fluid viscous dampers，NCEER-92-0032[M]．Buffalo，New York：National Center for Earthquake Engineering Research，1992．

[8]Constantinou M C，Soong T T，Dargush G F．Passive energy dissipation systems for structural design and retrofit monograph series[M]．Buffalo，New York：The Multidisciplinary Center for Earthquake Engineering Research，1998．

[9]中华人民共和国住房和城乡建设部.CJJ 166—2011 城市桥梁抗震设计规范[S]．北京：中国建筑工业出版社，2012．