激光波前相位测试与校准技术

刘　磊　胡绍云　孟庆安　张　浩　蒋泽伟

(1.安徽医科大学附属省立医院，合肥 23001；2.西南技术物理研究所，成都 610041)

0　引言

目前测量激光束波前相位的方法主要有两种，一种为波前传感器法，即利用经典Hartmann波前传感器、Hartmann-Shack波前传感器等测量激光束波前相位；另一种为剪切干涉法，即利用剪切干涉仪通过干涉原理测量激光束的波前相位。本文介绍了Hartmann-Shack波前传感器测量激光束波前相位的测试方法和测试原理。Hartmann-Shack波前传感器由一个微透镜阵列、CCD相机和数据采集处理系统三部分组成，可同时获得激光束的波前斜率和光束的近场强度分布，通过Zernike模式法或区域法重构可得到激光束的波前相位，广泛应用于自适应光学波前相位测量、激光光束质量测量和激光医学检测等工程领域。

Hartmann-Shack波前传感器可通过溯源至标准平面面形，然后将标准平面面形溯源至国家平面基准的方法实现校准。

1　测量原理

Hartmann-Shack波前传感器测量原理如图1所示。它主要由按一定规律排列的子透镜，即微透镜阵列、CCD和数据处理系统构成的。其基本原理是：待测光束经准直后作为参考光波，该参考光波通过微透镜阵列的每个子透镜，在CCD上形成一个与子透镜相对应的光斑阵列，将每个光斑的质心作为参考位置(基准)。当待测光束波前变化时，观察屏上每一光斑质心相对于各自质心的参考位置(基准)将有一位移。位置(i,j)的子透镜对应的光斑在x,y方向的位移分别为Δxij,Δyij,设子透镜与观察屏之间的距离为f，则子透镜上波前平均斜率gxij,gyij为

gxij=-Δxij/f

gyij=-Δyij/f

(1)

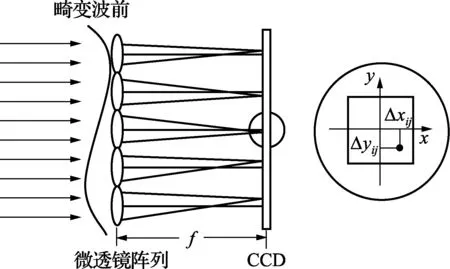
图1　哈特曼-夏克波前传感器原理示意图

求出畸变波前上被各阵列透镜分割的子透镜范围内波前的平均斜率，即可求得全孔径波前的光程差或相位分布。

用波前斜率这个信息，采用波前重构理论中的区域法或模式法就可以获得变形波像差。若以标准平面波为参考波，还可直接重构出光波前。

如何快速准确地测量透镜阵列焦面上的光斑质心坐标是Hartmann-Shack波前探测的核心问题，它直接影响到波前拟合的精度。常用的测定质心的方法有四象限法、CCD法等。下面主要介绍CCD法。

在微透镜阵列子孔径数增多的情况下，光电倍增管和四象限探测器之类的光敏组件用于波前探测，光敏组件将会变得越来越庞大而复杂，或由于灵敏度不能满足要求，而难以实际应用。随着高帧频低噪声的电荷耦合器件(CCD)和大容量高速度数字信号处理电路的发展，建立在他们基础上的探测器已广泛应用于多种传感器，包括Hartmann-Shack波前传感器。

根据光斑质心的定义可写出离散采样情况下的质心计算公式为

(2)

式中：xi，yi分别为CCD各单元(像素)中心点的坐标；Ii,j为第(i，j)个CCD单元接收的光能量；L，M分别为子孔径单元的长度和宽度值。

把CCD单元接收的光信号通过A/D转换后送入计算机，按式(2)就可算出各个子孔径光斑的质心坐标。

2　波前重构

一个完整的波前相位φ(x,y)的泽尼克正交多项式Zk展开为：

(3)

式中：D为泽尼克正交多项式矩阵；A为系数矩阵。式(3)是波前相位展开式的连续形式，实际的离散形式为：

(4)

再由波前斜率gx，gy与波前相位的关系，可得

(5)

式中：εx和εy为测量误差，由于波前传感器测量的是子孔径(i,j)内(对应面积为Si)的平均波前斜率，因此式(5)也应写成平均值形式：

(6)

(7)

式(6)、(7)用矩阵符号表示为

φ=DφAφ

(8)

G=DgAg+ε

(9)

式中：φ为m维向量；Dφ为n×m矩阵；Aφ为m维向量；G为2m维向量；Dg为2n×m维矩阵；Ag为2m维向量。

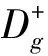
(10)

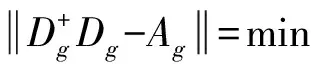
(11)

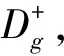
3　波前校准

3.1　校准方法

Hartmann-Shack波前传感器可通过一组标准平面溯源至国家平面基准，校准溯源图如图2所示，其溯源方法为：加工一组不同面形的平面玻璃作为标准平面，固定标准平面校准口径，将标准平面送检至国家平面基准，得到标准平面在固定波长固定口径下面形的峰谷值，将其作为校准标定值，然后用被校的Hartmann-Shack波前传感器测量同一波长同一口径下的标准平面的面形峰谷值，通过与校准证书上的校准标定值进行比对，达到对Hartmann-Shack波前传感器的校准。

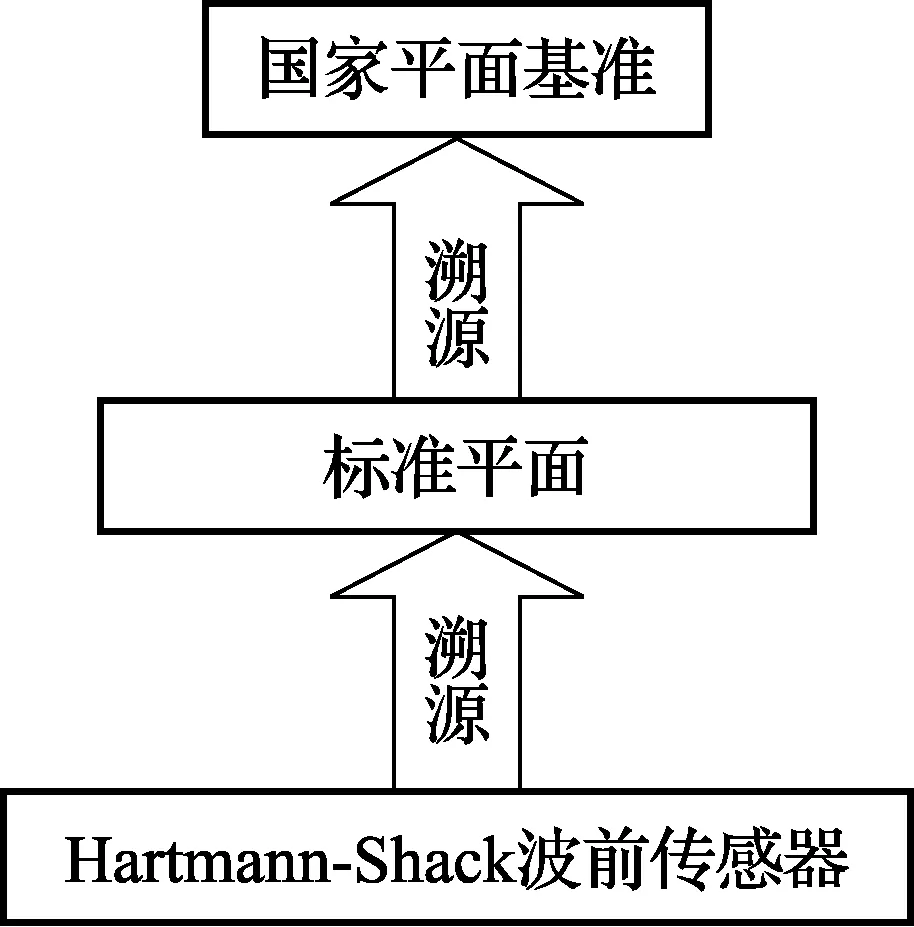
图2　Hartmann-Shack波前传感器校准溯源图

Hartmann-Shack波前传感器校准装置如图3所示，校准方法为：准直激光光源出射的激光束经衰减系统衰减后，经过分束器后到达高精度平面反射镜，高精度平面反射镜的面形峰谷值优于l/5(l=632.8nm)，激光被高精度平面反射镜反射后传至分束器，经分束器折射后到达Hartmann-Shack波前传感器靶面，开启波前传感器，测量此时的激光波前峰谷值，并把该波前值作为波前传感器的参考值；然后换下高精度平面反射镜，换上标定过的标准平面，用波前传感器测量标准平面的波前峰谷值，重复测量6次以上，计算其算术平均值作为标准平面的测量值，按式(12)计算被校波前传感器的波前峰谷值示值误差。

(12)

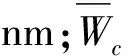
用波前峰谷值示值误差评估被校波前传感器在固定波长、固定面形水平下是否满足说明书指标要求或客户使用要求，完成对Hartmann-Shack波前传感器在该面形值下的校准。在Hartmann-Shack波前传感器面形测量范围内，通过测量不同面形的标准平面的面形峰谷值，并与校准证书标定值进行比对，达到对Hartmann-Shack波前传感器全范围的校准。

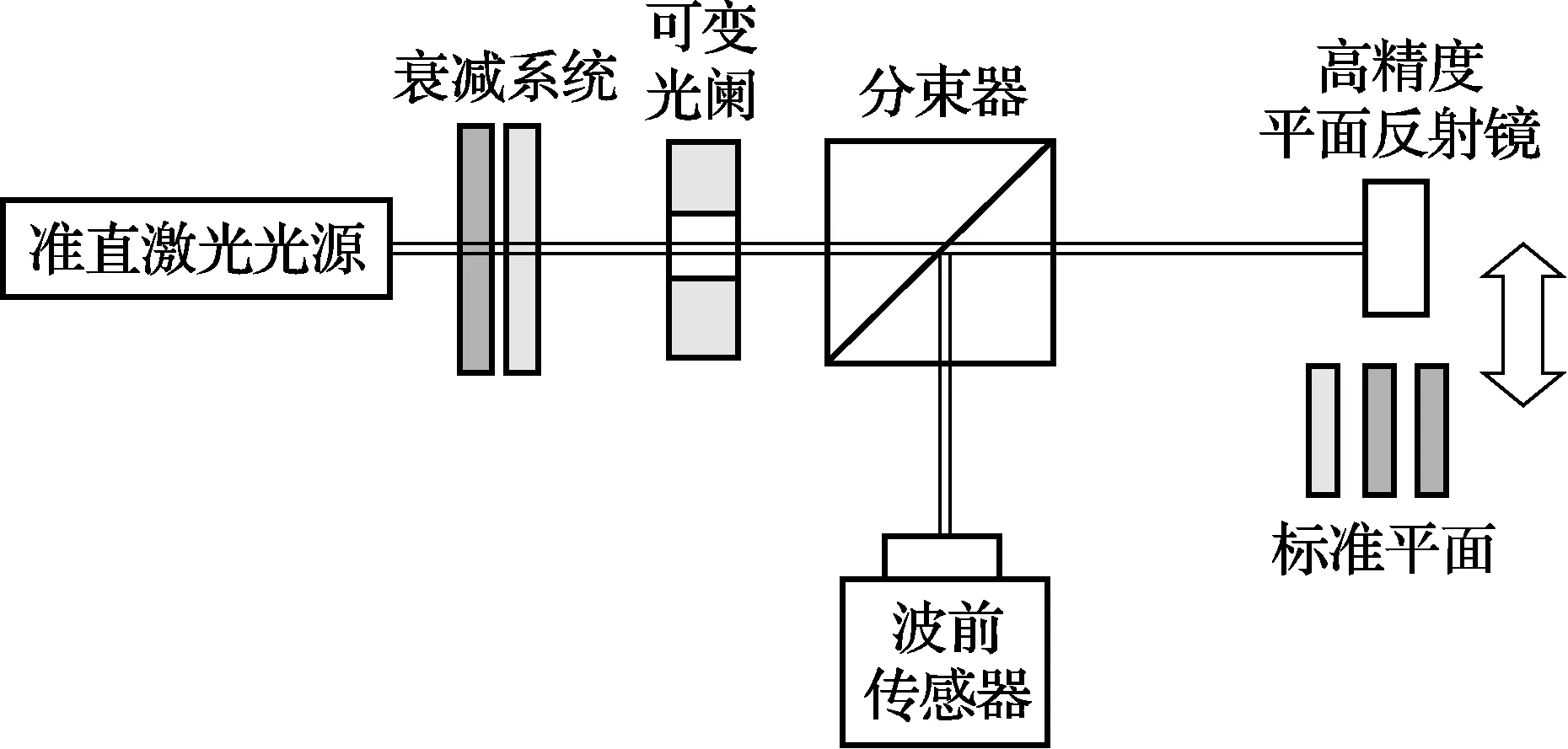
图3　Hartmann-Shack波前传感器校准装置示意图

3.2　校准实验

实验选用3块不同面形峰谷值的标准平面，标准平面口径均为Ф15mm，上级计量机构给出的在校准波长632.8nm、校准口径Ф15mm的峰谷值分别为：0.682l，0.864l，1.039l，实验选用的被校波前传感器为美国Wavefront公司生产的CLAS-2D波前传感器；准直激光光源的波长为632.8nm，光斑直径Ф50mm，光斑直径可通过光路中的可变光阑调节，调节范围为Ф1～Ф50mm；高精度平面反射镜选用高精度平面平晶，经上级计量机构校准得到在632.8nm波长下的峰谷值为l/30。根据校准方法搭建实验装置，进行校准实验，实验测得被校波前传感器测得3块校准峰谷值分别为0.682l，0.864l，1.039l的标准平面在波长632.8nm、口径Ф15mm的波前峰谷值示值误差分别为0.093l，0.106l，0.962l。在3种面形条件下，被校波前传感器的波前峰谷值示值误差均小于l/10(l=632.8nm)，满足说明书技术指标要求。

3.3　不确定度分析

根据校准方法，影响校准结果的不确定度分量主要有：标准平面送上级计量机构校准引入的不确定度u1；高精度平面反射镜面形引入的不确定度u2。

标准平面送上级计量机构校准引入的不确定度u1采用B类不确定度评定方法评定，可由上级计量技术机构给出的校准证书查得。由校准证书查得标准平面校准的扩展不确定度为U=10nm，包含因子k=2，则标准平面镜面形峰谷值校准引入的不确定度为：

u1=10/2=5nm

高精度平面反射镜面形引入的不确定度u2采用B类不确定度评定方法评定，可由上级计量技术机构给出的检定证书查得，其计算公式为

u2=Ws+U/k

(13)

由证书查得实验用的高精度平面反射镜面形偏差峰谷值校准值为21nm，其测量扩展不确定度为U=10.0nm，包含因子为k=2，则标准平晶面形误差引入的不确定度为

u2=21+10/2=26nm

以上2个影响分量独立不相关，因此Hartmann-Shack波前传感器校准合成标准不确定度的计算公式为

(14)

4　结论

Hartmann-Shack波前传感器具有结构简单、稳定和对环境条件要求低的特点，是理想的激光波前相位测量设备，并且可同时获得激光束的远场分布特征。为提高激光波前测量结果的准确度，必须定期对Hartmann-Shack波前传感器进行校准，本文创新性地提出了用不同面形的标准平面对Hartmann-Shack波前传感器进行校准的方法，该方法可将其量值溯源至国家平面基准。根据校准方法搭建了实验装置，进行了校准实验，并对校准结果的不确定度进行了分析。通过校准保证了Hartmann-Shack波前传感器测量激光波前相位的准确性，其测量结果可为激光器的研制和运行提供重要的导向参数。

[1]鲜浩，李华贵，姜文汉，等.用Hartmann-Shack传感器测量激光束的波前相位.光电工程，1995，22(2)：38-45

[2]胡美鹏.示值误差不确定度按测量范围并用被测参数的函数表示.计量技术，2014(1)

[3]朱彬，许冰，胡渝.Hartmann-Shack传感器在光束质量测量中的应用.激光杂志，2001，22(2)：34-35

[4]常宗英，侯美桃.简化计算测量不确定度合成形式.计量技术，2013(1)

[5]陈哲，胡永明，常胜利，等.一种重构高功率激光束波前的方法.光学学报，1999，19(3)：327-333

[6]周仁忠，著.自适应光学.北京：国防工业出版社，1996

[7]邵建新，刘云虎，张子英，等.测量结果及其不确定度有效位数确定问题.计量学报，2013，34(3)

[8]刘兰琴，张清泉，景峰，等.两种不同算法重现高功率激光束的相位.强激光与离子束，2001，13(1)：34-38